
- •1. Аксиоматика 3
- •2. Множества 4
- •3. Аналитическая геометрия 14
- •4. Векторная алгебра 25
- •5. Матрицы и определители 30
- •Аксиоматика
- •Аксиоматический метод построения математики
- •Математический язык
- •Множества
- •Понятие множества
- •Пустое множество
- •Числовые множества
- •Подмножества
- •Пересечение множеств
- •Объединение множеств
- •Вычитание множеств
- •Аналитическая геометрия
- •Система координат на плоскости и в пространстве
- •Расстояние между двумя точками на плоскости
- •Уравнение линии. Уравнение прямой с угловым коэффициентом
- •Уравнение – уравнение прямой с угловым коэффициентом k
- •Общее уравнение прямой
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две данные (различные) точки и
- •Полярные координаты
- •Угол между прямыми
- •Уравнение окружности
- •Эллипс. Каноническое уравнение эллипса
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •У равнение сферы
- •Векторная алгебра
- •Понятие вектора
- •Коллинеарные векторы
- •Операции над векторами
- •Угол между векторами
- •Проекция вектора на ось
- •Скалярное произведение двух векторов
- •Координаты вектора
- •Разложение векторов
- •Действия над векторами, заданным координатами в пространстве
- •Матрицы и определители
- •Матрицы
- •Определители
- •Определители третьего порядка
- •Миноры и алгебраические дополнения матрицы
- •Обратная матрица
- •Системы линейных уравнений
- •Формулы Крамера
- •Матричный способ решения систем линейных уравнений
- •Метод Гаусса
- •Функции
- •Понятие функции
- •Способы задания функции
- •Обзор элементарных функций и их графиков
- •Пределы
- •Предел последовательности
- •Предел функции
- •Непрерывность функции
- •Производная
- •Определение производной
- •Правила дифференцирования
- •Производные высших порядков
- •Применение производной для исследования функции
- •Неопределенный интеграл
- •Способы интегрирования
- •О пределенный интеграл
- •Дифференциальные уравнения
- •Основные понятия:
- •Признаки сходимости ряда:
- •Ряды по степени разности
- •Теория вероятностей
- •Основные понятия теории вероятностей
- •Классическое определение вероятности
- •Геометрические вероятности
- •Алгебра событий
- •Теорема сложения вероятностей двух несовместимых событий
- •Теорема умножения вероятностей.
- •Теорема сложения вероятностей совместимых событий
- •Формула полной вероятности
- •Теорема умножения вероятностей независимых событий:
- •Дискретные случайные величины
- •Закон распределения дискретных случайных величин
- •Функция распределения случайной величины
- •Нормальное распределение
- •Числовые характеристики случайных величин
- •Свойства математического ожидания (мо) дискретной случайной величины:
- •Дисперсия дискретной случайной величины
- •Среднее квадратичное отклонение (стандартное)
- •Системы двух случайных величин и их числовые характеристики
- •Литература
Проекция вектора на ось
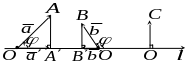 Проекцией
вектора
на ось
называется вектор
Проекцией
вектора
на ось
называется вектор
![]() ,
находящийся между началом вектора
и основанием перпендикуляра, опущенного
из конца вектора
на ось
.
,
находящийся между началом вектора
и основанием перпендикуляра, опущенного
из конца вектора
на ось
.
Проекция вектора на ось равна произведению его модуля на косинус угла между векторами и осью. Действительно:
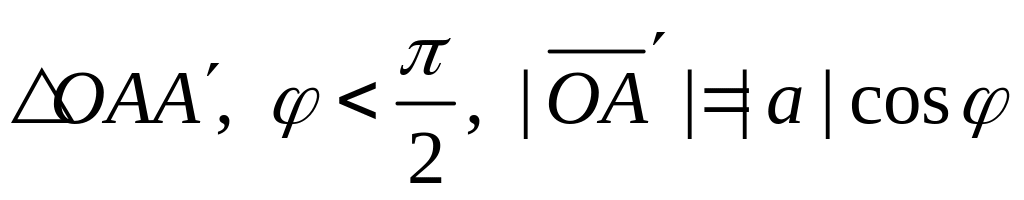 ;
; ;
;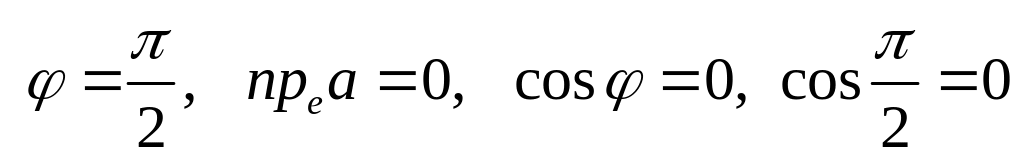 .
.
Следствие:
проекция вектора
на ось положительна, если
![]() (угол острый); отрицательна, если угол
тупой; равна нулю, если угол прямой.
(угол острый); отрицательна, если угол
тупой; равна нулю, если угол прямой.
Скалярное произведение двух векторов
Скалярным
произведением двух
векторов называется произведение их
модулей на косинус угла между ними. Оно
обозначается
![]() .
.
![]() – есть проекция
на
и
– есть проекция
на
и
![]() – проекция
на
.
Скалярное произведение векторов есть
произведение одного из них на проекцию
другого на первый. Косинус угла между
векторами:
– проекция
на
.
Скалярное произведение векторов есть
произведение одного из них на проекцию
другого на первый. Косинус угла между
векторами:
![]()
Два
вектора
на
перпендикулярны (ортогональны), т.е.
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
Свойства скалярного произведения:
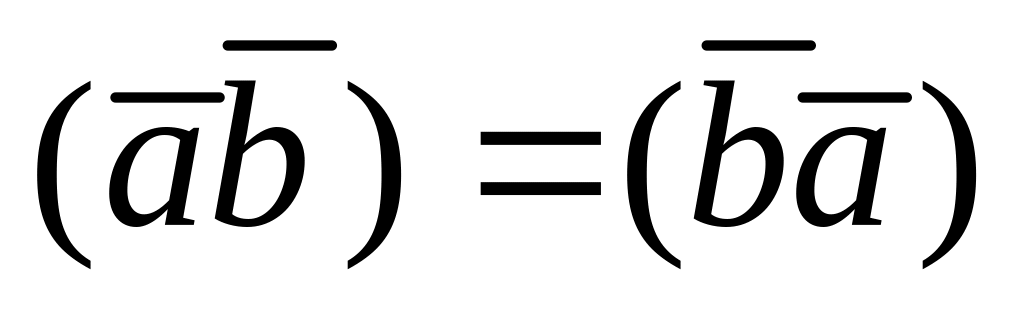 – переместительное
свойство;
– переместительное
свойство;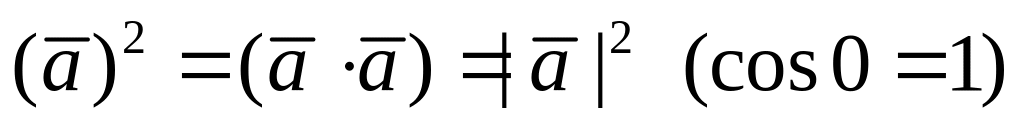 – скалярный
квадрат вектора;
– скалярный
квадрат вектора;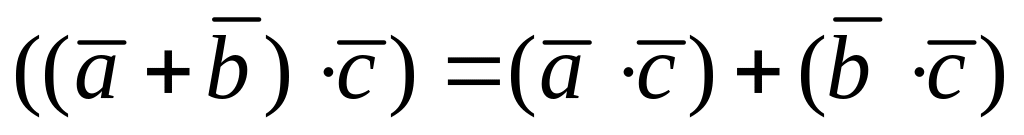 – распределительное
свойство;
– распределительное
свойство;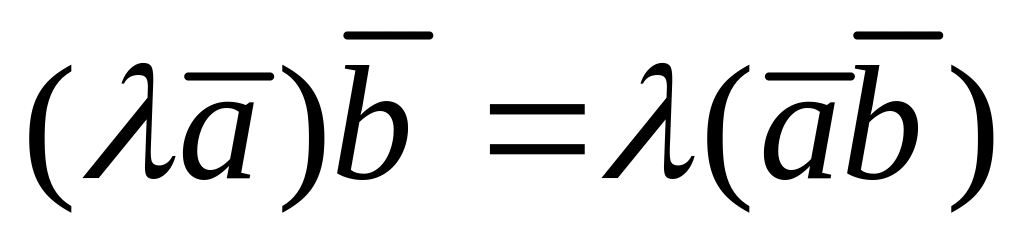 – сочетательное
свойство относительно числового
множителя.
– сочетательное
свойство относительно числового
множителя.
Координаты вектора
Н
 а
плоскости.
Если вектор задач двумя точками
а
плоскости.
Если вектор задач двумя точками
 и
и
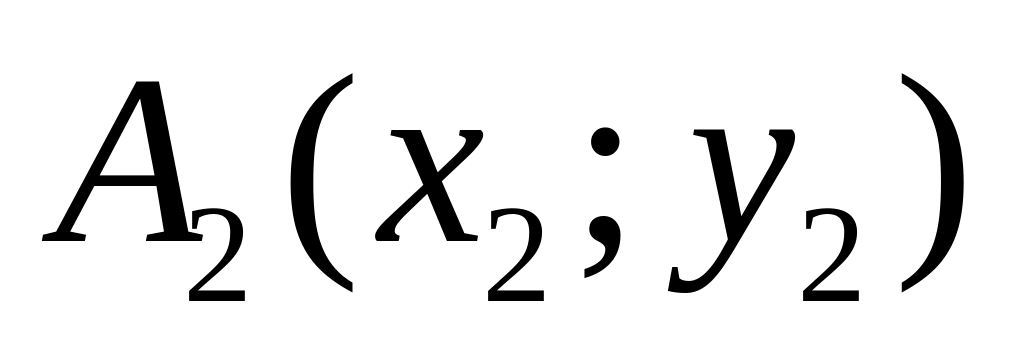 ,
то вектор
,
то вектор
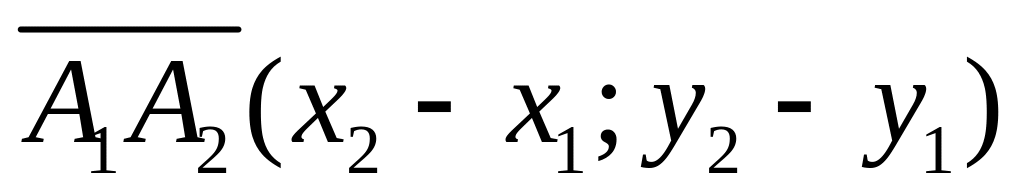 – способ задания вектора его координатами.
Модуль вектора
– способ задания вектора его координатами.
Модуль вектора
 .
.Координаты вектора в пространстве. Единичные векторы осей называются ортами:
 .
Если векторы в пространстве лежат в
одной плоскости или параллельны одной
плоскости, то они называются компланарными.
.
Если векторы в пространстве лежат в
одной плоскости или параллельны одной
плоскости, то они называются компланарными.
Так как орты – некомпланарные векторы, то они образуют базис. Базисом в пространстве называются три линейно независимых вектора.
Разложение векторов
На плоскости. Пусть даны три вектора , и . Разложить вектор по направлениям и . Через
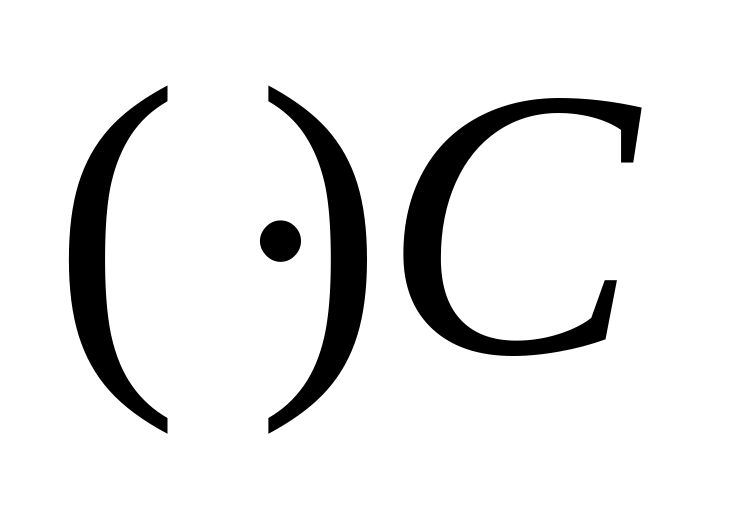 проводим
прямые параллельные
и
до пересечения с их направлениями.
Получаем
и
проводим
прямые параллельные
и
до пересечения с их направлениями.
Получаем
и
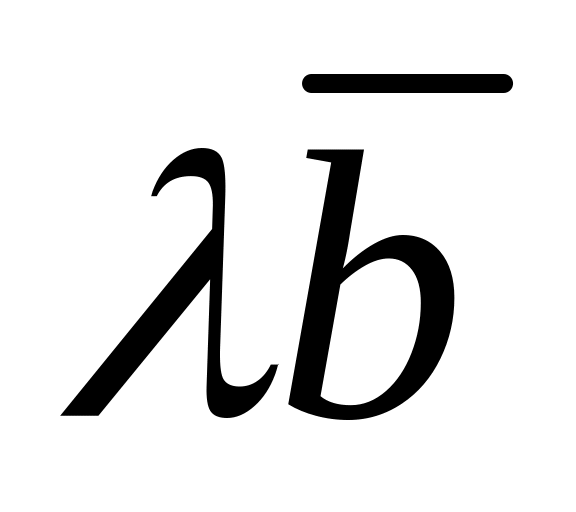 :
:
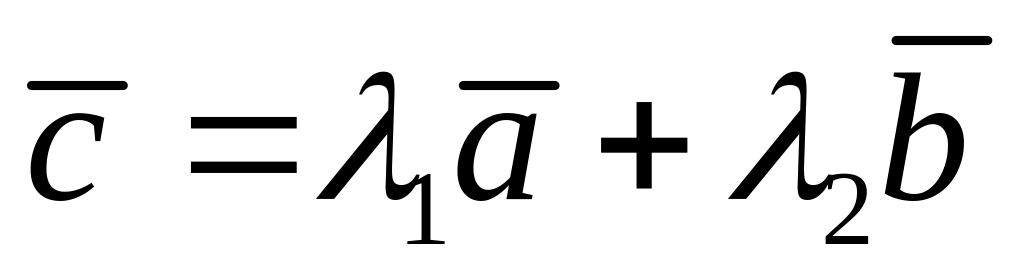 .
.В пространстве:
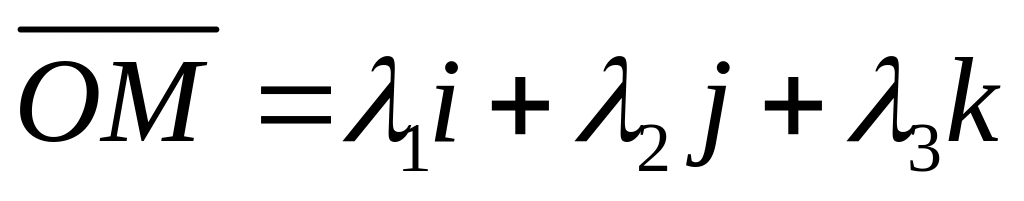 .
.
![]()
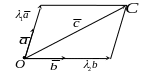
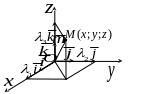 – вектор,
который надо разложить по векторам
,
и
.
– вектор,
который надо разложить по векторам
,
и
.
Действия над векторами, заданным координатами в пространстве
При сложении векторов, заданных координатами, соответствующие координаты складываются:
 .
.При умножении вектора на число его координаты умножаются на это число:
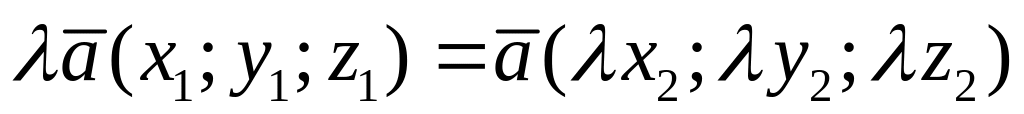 .
.Скалярное произведение векторов равно сумме парных произведений их одноименных координат:
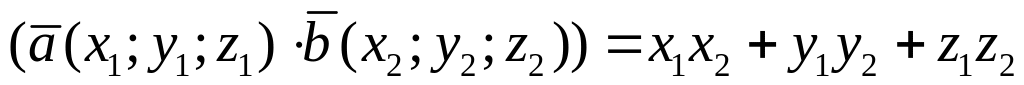 .
.Косинус угла между векторами
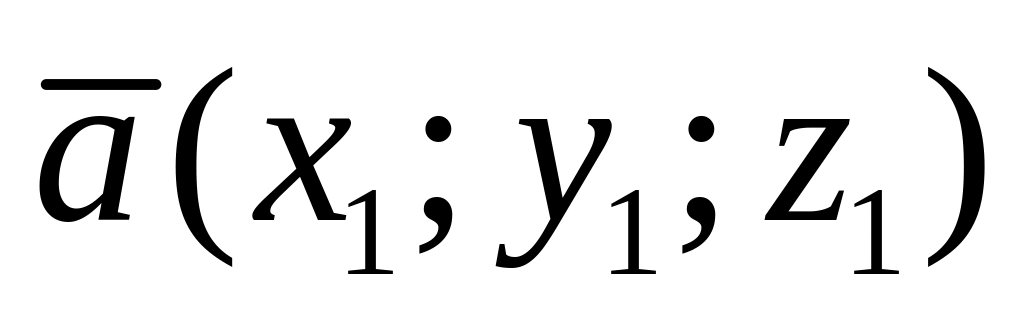 и
и
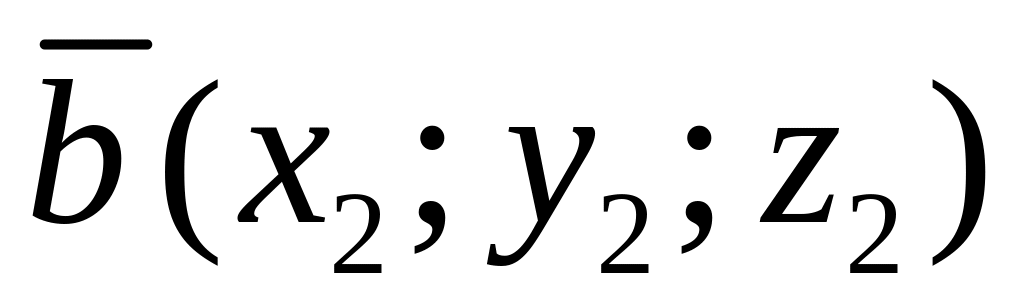 в пространстве находится по формуле:
в пространстве находится по формуле:
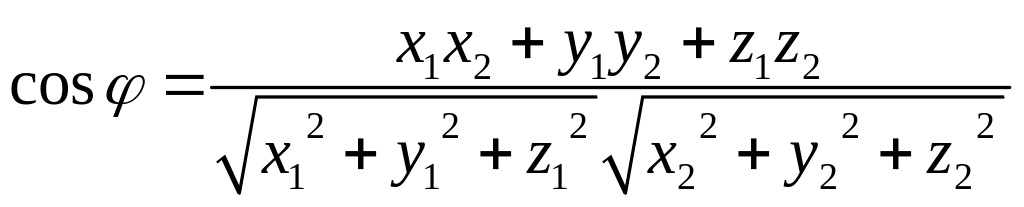 ,
где
,
где
![]() – длина
вектора
– длина
вектора
![]() ;
;
![]() – длина
вектора
– длина
вектора
![]() .
.
Матрицы и определители
Матрицы
Определение:
таблица
чисел
![]() вида, состоящая из
вида, состоящая из
![]() строк и
столбцов называется матрицей.
строк и
столбцов называется матрицей.
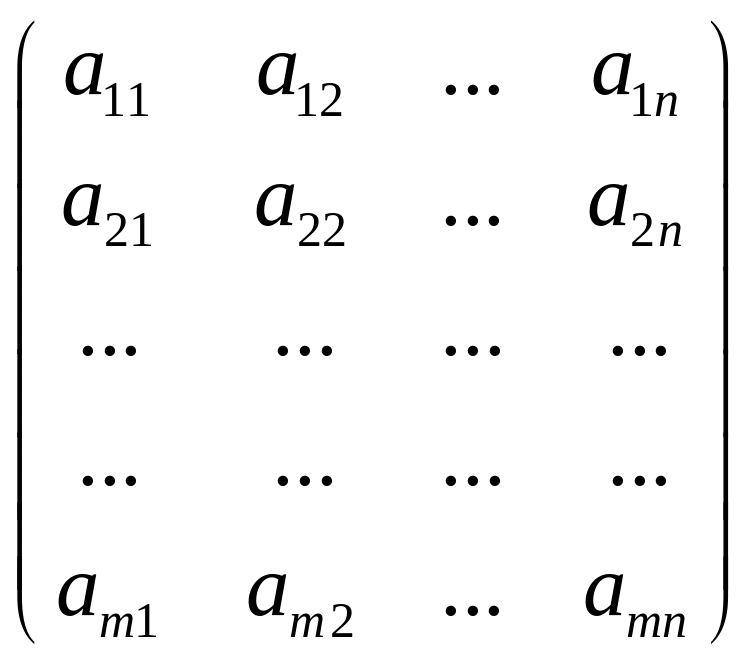
Числа
называются элементами
матрицы.
Написанная выше матрица – прямоугольная.
Если в матрице число строк равно числу
столбцов
![]() ,
то такую матрицу называют квадратной,
а число строк или столбцов – порядком
матрицы.
,
то такую матрицу называют квадратной,
а число строк или столбцов – порядком
матрицы.
Например
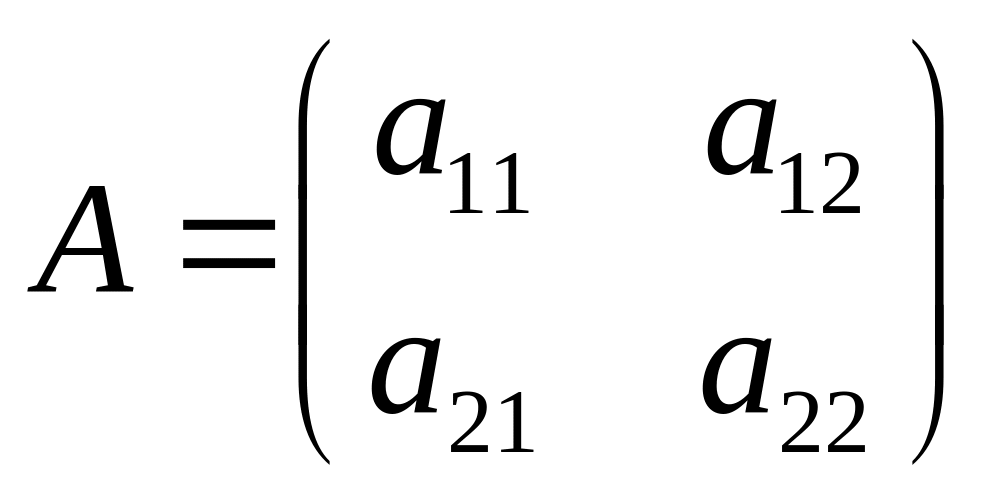 – квадратная матрица
второго порядка.
– квадратная матрица
второго порядка.
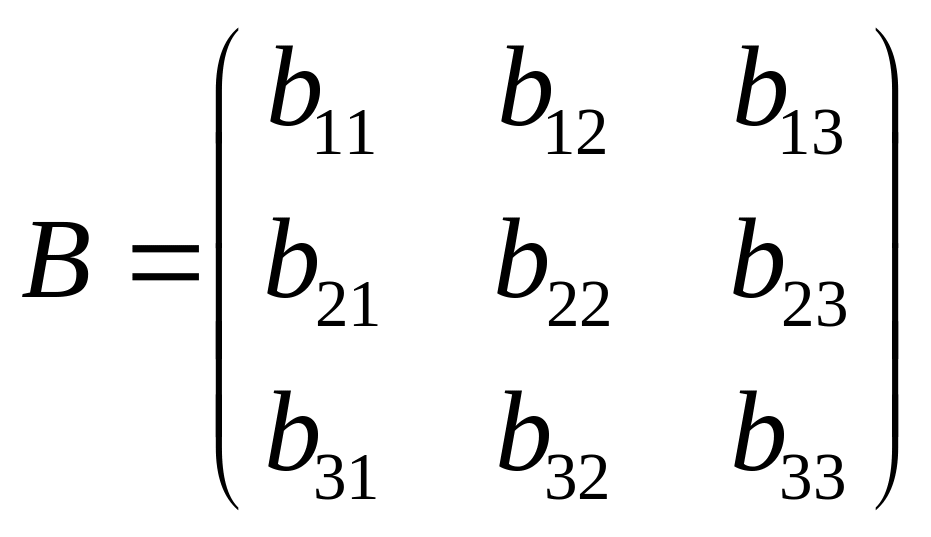 – квадратная
матрица
третьего порядка.
– квадратная
матрица
третьего порядка.
Если матрица состоит из одной строки, то это матрица-строка; из одного столбца – матрица-столбец.
Две матрицы называются равными, если они одинакового порядка и все элементы равны.
Матрица, все элементы которой нули, называется нуль-матрицей.
Сложение матриц.
Матрицы
одинакового размера можно складывать.
Суммой матриц называется такая матрица,
элементы которой равны сумме
соответствующих элементов слагаемых
матриц:
![]() .
.
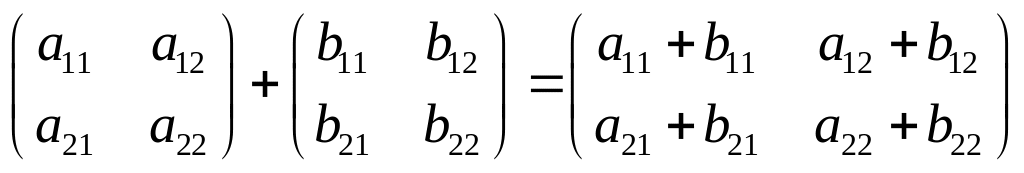
Вычитание матриц
Матрицы
одинакового порядка можно вычитать.
Разностью
двух матриц
и
одинакового порядка называется такая
матрица
,
что
![]() .
Из определения следует, что элементы
матрицы
равны разности соответствующих элементов
матрицы
и
:
.
Из определения следует, что элементы
матрицы
равны разности соответствующих элементов
матрицы
и
:
![]() .
.
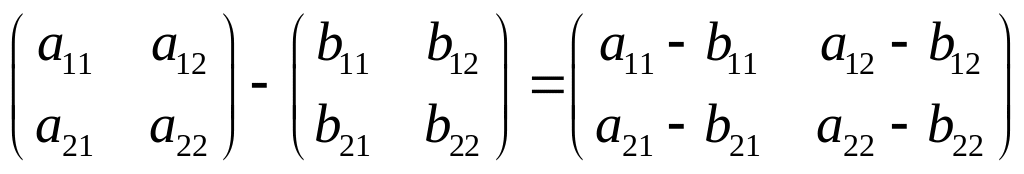
Умножение матрицы на число
Произведением матрицы на число называется матрица, элементы которой равны произведению числа на ее соответствующие элемент. При умножении матрицы на нуль получается нуль-матрица.
Умножение матриц
Пусть даны две матрицы:
и
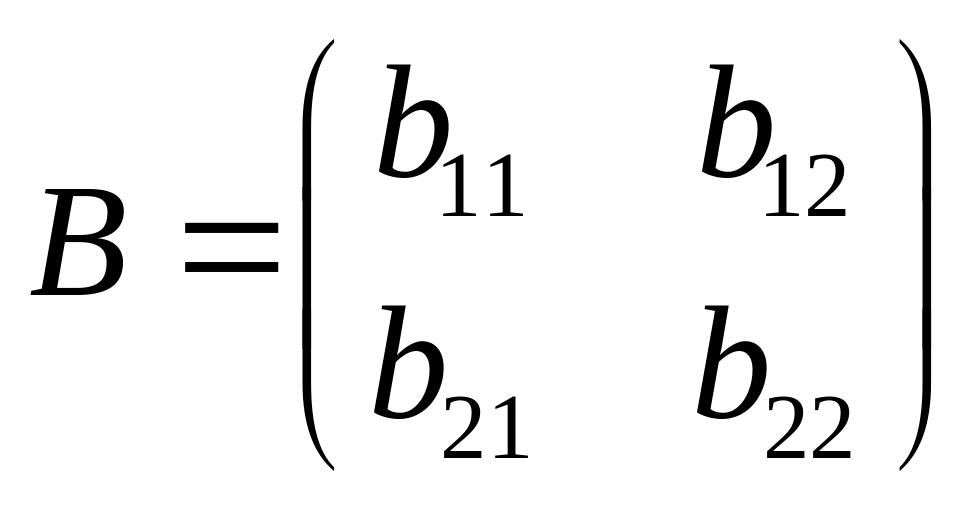 .
Найти матрицу
.
Найти матрицу
![]() ?
?
Каждый элемент новой матрицы, находящийся на пересечении i-ой строки и k-го столбца представляет собой сумму парных произведений элементов i-ой строки первой матрицы на элементы k-го столбца второй матрицы.

Это правило сохраняется для умножения прямоугольных матриц, в которых число столбцов матрицы-множимого равна числу строк матрицы-множителя. В результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое и столько столбцов, сколько их имеет матрица-множитель.
Особое
значение имеет матрица
![]() ,
которая называется единичной,
при умножении матрицы
на
,
которая называется единичной,
при умножении матрицы
на
![]() получится
.
получится
.
Законы умножения матриц:
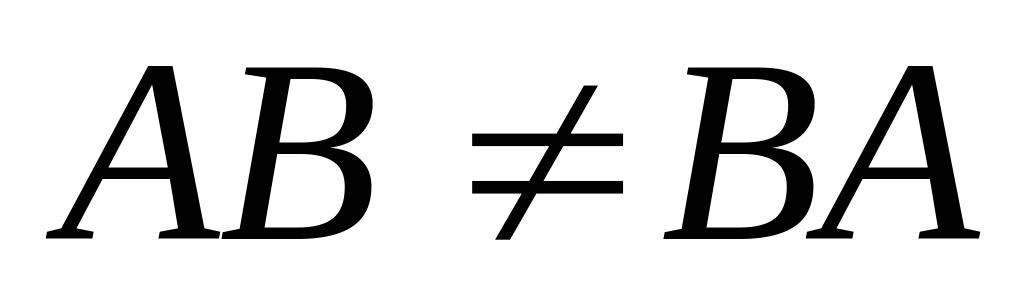 (переместительный
закон не выполняется);
(переместительный
закон не выполняется);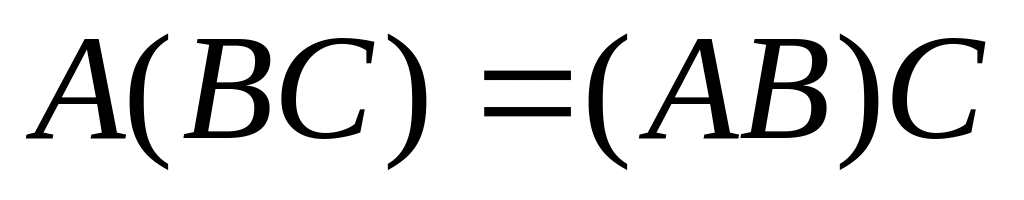 (сочетательный
закон выполняется).
(сочетательный
закон выполняется).
