§ 8. Степенная функция с целым отрицательным показателем

Определение. Степень действительного числа a с целым отрицательным показателем определяется формулой:

(пN).

Полагая для , получаем, что для действительного числа а понятие степени определено для любого целого п (кроме случая 0⁰).

Свойства степени с целым показателем

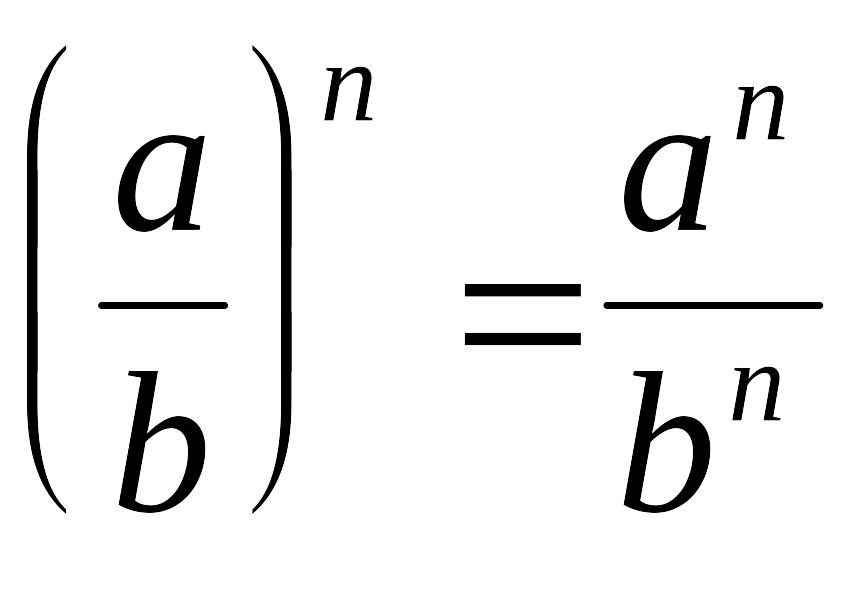
Свойства функции ,

Поскольку по определению ( ), то свойства функции легко выводятся из свойств степенной функции с натуральным показателем п.

1. Область определения. .

2. Нули функции, промежутки знакопостоянства. Очевидно, нулей у функции нет. Если n четно, то для любого . Если n нечетно, то на и на .

3. Непрерывность. Функция непрерывна на своей области определения как частное непрерывных функций.

4. Четность, нечетность.

Предложение Функция , является четной, если n четно, и нечетной, если n нечетно.

Доказательство. – симметричное относительно нуля множество.

Далее воспользуемся свойствами четности и нечетности степенной функции с натуральным показателем при четном и нечетном п соответственно.

Пусть п четно.

Тогда для любого . Следовательно, – четная функция при четном п.

Пусть п нечетно.

Тогда для любого . Следовательно, – нечетная функция при нечетном п.

5. Монотонность.

Предложение. Функция , ,

1. на 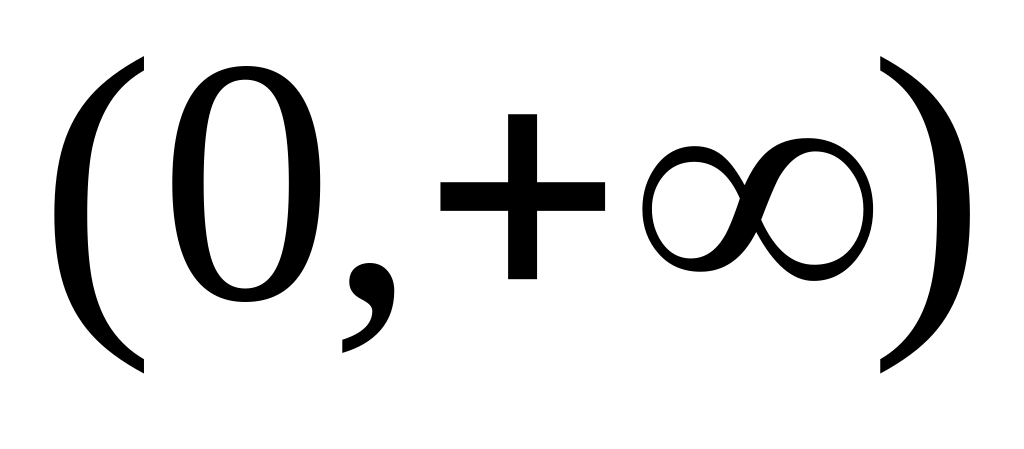строго убывает,

2. на 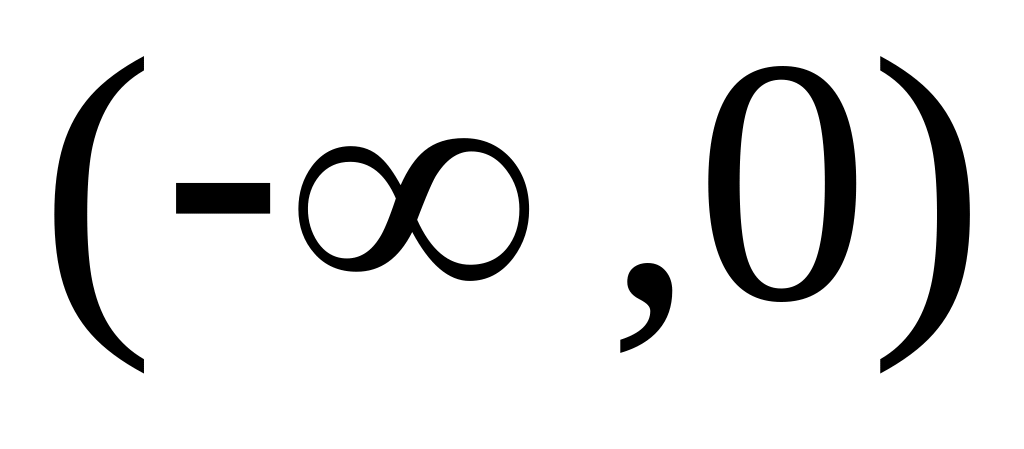строго возрастает при четном п и строго убывает при нечетном п.

Доказательство. Воспользуемся свойствами монотонности степенной функции с натуральным показателем (§7, п.5).

1) Пусть х₁ и х₂ – произвольные точки из , удовлетворяющие неравенству х₁ < х₂. Так как функция , , строго возрастает на , то . Отсюда , т. е. . Таким образом, . Следовательно, функция , , строго убывает на .

2) Доказывается аналогично.

6. Асимптоты функции.

Предложение. Прямая у=0 является горизонтальной асимптотой функции ( ).

Доказательство. По свойствам степенной функции с натуральным показателем и теореме о связи между бесконечно большой и бесконечно малой функциями получаем: .

Предложение доказано.

Предложение. Прямая х=0 является вертикальной асимптотой функции ( ).

Доказательство. Поскольку для любого натурального п, то . При этом односторонние пределы в точке 0 равны:

при любом ,

7. Множество значений.

Предложение.

Доказательство. Пусть п четно. Поскольку все значения функции положительны, то остается доказать, что любое число является значением функции f. Пусть – произвольное действительное число. Выше доказано (см. §7, п. 8), что множеством значений функции является . Следовательно, существует точка , для которой . Тогда , т. е. . Следовательно, .

При нечетном п рассуждения аналогичны.

8. Ограниченность.

Так как множество значений функции ( ) является неограниченным сверху числовым множеством, то функция f неограниченна сверху при любом п, и, следовательно, неограниченна. Кроме того, , если п четно, – ограниченное снизу множество и , если п нечетно, – неограниченное снизу множество. Следовательно, функция f ограниченна снизу при четном п и неограниченна снизу при нечетном п.

9. График функции. , .

п нечетно

При п=1 получаем функцию , которая называется обратной пропорциональностью. Графиком этой функции является гипербола.