3. Периодичность.

Предложение. Функция является периодической с основным периодом .

Доказательство. Поскольку длина единичной окружности равна 2, то числам  и +2 соответствует одна и та же точка М на единичной окружности. Поэтому 2 является периодом функции . Докажем, что это основной период, т. е. никакое положительное число меньшее 2 периодом функции косинус не является. Пусть . Сравним значения функции косинус в точках 0 и Т. Углу 0 радиан соответствует точка (1,0) на единичной окружности, т.е. . Так как Т меньше длины единичной окружности, то углу соответствует точка единичной окружности, отличная от (1,0). Значит, . Таким образом, . Это показывает, что никакое число Т, , не является периодом функции косинус.

Предложение доказано.

4. Нули функции, промежутки знакопостоянства. Рассмотрим уравнение . Прямая х=0 пересекает единичную окружность в точках (0, –1) и (0,1), которым соответствуют углы –/2 и /2. Учитывая периодичность функции косинус, получаем:

.

Поскольку все точки единичной окружности, расположенные в I и IV координатных четвертях, имеют положительные абсциссы, а точки, расположенные в II и III четвертях, – отрицательные абсциссы, то

,

.

5. Четность, нечетность.

Предложение. Функция является четной.

Доказательство. Углам  и – соответствуют симметричные относительно оси ОХ точки на единичной окружности. Поэтому их абсциссы равны, т.е. для любого .

6. Непрерывность.

Предложение. Функция непрерывна на R.

Доказательство. Пусть х₀ – произвольная точка числовой прямой. Воспользуемся определением непрерывности функции в точке на языке приращений. Придадим аргументу ненулевое приращение х. Тогда функция получит приращение

.

Пользуясь леммой и ограниченностью синуса, получаем:

.

Из неравенства и теоремы о пределе промежуточной функции имеем . Следовательно, функция непрерывна в точке х₀. Так как х₀ – произвольная точка числовой прямой, то функция непрерывна на R.

Следовательно, f – нечетная функция.

7. Монотонность.

Предложение. Функция

1) строго возрастает на промежутках ,

2) строго убывает на промежутках .

Доказательство. Опираясь на свойство периодичности, достаточно доказать, что функция строго возрастает на и строго убывает на . Докажем ее возрастание на . Возьмем произвольные точки и , такие что . Покажем, что разность значений функции в этих точках положительна. Из неравенств , и получаем и . Для этих значений аргумента и , следовательно, , т.е. . Тем самым доказано, что функция строго возрастает на .

Докажем, что функция убывает на отрезке . Для произвольных точек и в этом случае из неравенств , и следует и . Тогда и , следовательно, . Получили . Тем самым доказано, что функция строго убывает на .

8. Экстремумы функции . Так как функция возрастает на промежутках и и убывает на промежутке , то 0 – точка максимума функции косинус, а  – ее точка минимума. В силу периодичности функции получаем, что точки являются точками максимума, а точки – точками минимума функции .

9. График функции также называется синусоидой.

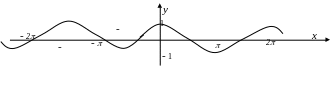
Замечание. Из формул приведения известно, что для любого действительного х. Поэтому свойства функции могут быть получены как следствия свойств функции синус.