Василек

11. Расчет статистической суммы для классического одноатомного идеального газа. Нахождение ТД ф-ций и ТД ур-я состояния системы. всякое исследов теории начинают с модели сист. При этом модель может приближенно или точно отражать все качества реального объекта. Простейшей системой явл ид газ. Каждую частицу мы можем моделировать матем точкой т.к газ одноатомный. Газ заперт в некотором объеме назначение стенок не выпускать частицы наружу, а чтобы стенки не мешали расчету, чтобы не учитывать краевые условия будем считать что столкновения упругие. На первый раз полагаем, что никаких других внеш полей нет. По определению газ называют идеальным если нет взаимод м.у частицами. На самом деле мы просто считаем, что взаимод-е прходило мало, если бы вообще не было взаимодействий, то каждая частица двигалась сама по себе и присут-ие других молекул для нее было бы не заметно. Следствие: энергия сист равна сумме энергий всех частиц. Будем предполагать что частицы дв-ся по законам класс мех-ки. Предположим что газ равновесен и с пом-ю термостата Т-постоянна. Найдем энергию газа как функцию(T,V,N) тогда р=Р(Т,V,N). Зная Е и р рассчитаем остальное. Применим каноническое распределение и все вытекающие формулы. Расчет ТД хар-к начинается с вычисления стат суммы. Стат сумма будет вычисляться в квазиклассическом виде т.к. система практически классическая. Множитель добавить легко; в классической физике всё равно интеграл надо множить на какую то константу чтобы получить безразмерную величину под логарифмом; квантовая Т подсказывает какая должна быть конст; без этого множителя не получиться правильной зависимости энерг от числа частиц. Рассмотрим инт-л. В качестве обощенных коэфф выделим x, y, z. Интегрир по коорд отделяется от интегр по импульсу. Пределы изменения переменных огранич стенками сосуда. Коэффициенты каждой частицы не связаны с коэфф других частиц. Легко сообразить что инт-л по имп разбивается на ряд множителей однотипных по структуре т.к. exp можно разбить произведением exp. -для каждой частицы. Имеется сложность вычисления отдельного инт-ла т.к. энергия всего газа постоянна, она складывается из имп отд частиц, имп зависят др. от др. Но мы можем взять пределы от - до . -энергия на одну степень свободы может быть=0 и равна всей энерг газа( Нахождение ТД хар-к идеал газа. Стат сумма предст собой функцию z =z(T,V,N) Т.к. N>>1 тогда применим ф-лу Стирлинга . Все последующие члены мы отбросим. тогда найдем вид U,S,F: Посмотрим что будет с S, если Т0 тогда S= -, это противоречит 3 началу ТД(S должна стремиться к 0) это связано с тем, что мы пользовались класс физикой, а при низких тем-х она неприменима. . Остаётся найти р В этой области и другие выражения явл неверными Совпадение выведенного термического ур-я с эмпирическим ур-ем Менд-Клапей явл подтверждением стат теории, с др. стороны сделанный вывод предст собой теор обоснование ТД формулы ур-я сост идеал газа.

12. Распределение Максвелла-Больцмана. Распределение Максвелла и его свойства. Распределение для модуля скорости и энергии частицы. Распределение Больцмана. Барометрическая ф-ла. Изуч сист- класс идеал одноатомн газ мы будем считать для общности, что газ помещен во внешн силовое поле U(r), каждая частица газа связана с внешним полем отдельно самостоятельно. Поэтому U(r) есть потенциальная энергия одной частицы находящейся в точке r. Поставим вопрос как найти вер-ть того, что частица обладает имп-ом и находится в точке r. Используем каноническое распределение Записанное в таком виде оно отвечает на вопр какова вероят попадания в 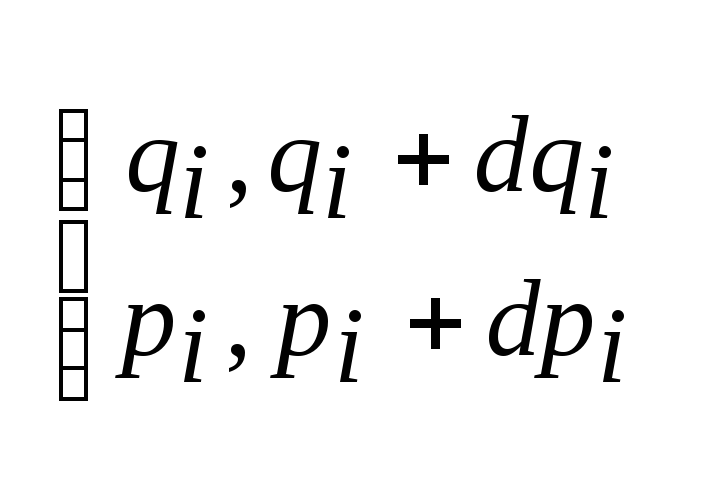i=0,1,2... Число степеней свободы  велико, поэтому незнаем как выделить отсюда информацию об одной частице. Будем использовать обобщенные координаты . Первая сумма есть сумма кинетических энергий частиц, вторая- сумма потенциальных энергий(поскольку они взаимод с внешним полем). Энергия распадается на ряд слагаемых, которые зависят от коорд и имп-ов только одной частицы. Соответ экспонента распадается на . Это означает, что наше распределение по коорд и имп всех частиц распадается на произведения распредел коорд и имп отдел частиц dW(x,y)=(x)(y)dxdy dW(x)= (x)dx dW(y)= (y)dy  dW(x,y)= dW(x)dW(y). Такое распадение возможно если отдельные частицы распред независимо др от др. В данном случае это отражает физику- взаимодействия между частицами на расстоянии нет и поэтому их можно рассматривать как квазинезависимые др по отнош к др. Поэтому мы легко можем из общего распред выписать распред для одной час-цы. В силу равноправия частиц они все имеют одинаковую стр-ру . Действительно нормировочный интеграл I тоже можно представ в виде произв множит однотипных с интегралом стоящим в послед форм-ле. Записанное распред наз-ся распред Максвелла-Больцмана, оно легко разбивается на 2 распред-я. Т.е. имеются 2 независимых распред для коорд и имп. Физика- мы полагаем, что потенциальная энергия есть функц только коорд, а кинет в клас физике зависит только от имп и никогда от коорд. dW(p)- распред Максвелла, dW(r)- распред Больцмана. распределение Максвела: характерно своей универсальностью. Оно применимо не только к ид газу но и к любой сист точечных класич част. Потому что кинет энергия всегда зависит от импульсов. 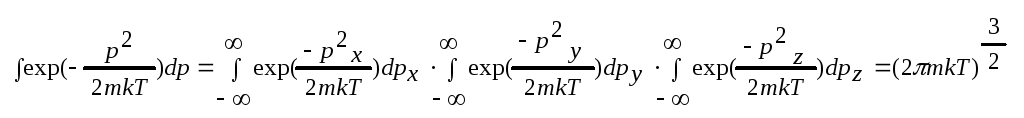.интеграл стоящий в знаменателе легко вычислить очень часто вместо импульса использ скорость Максв распред можно считать статис незав. Распред-е по скоростям и энерг. Распр-е по имп-сам легко преобр в распр по скорост его можно предст-ть в виде произ-я трех распред-ий вероятности для проек-й скорости формула свидетельствует о статис незав-ти всех трех проекций скорости, тогда для модуля скорости получим и наконец если использовать то получим распред-е вероят-ей для значений энергии свободн частицы. Распред-е Больцмана В отличие от М. распред-я распределение Больцмана для каждой задачи будет свое т.к оно зависит от вида ф-ии U(r), т.е оно не универсально. 1)тогда вид распред показыв что все точки внутри сосуда явл равновероятными.2) U(r)=mgz однородное гравит поле. По коорд-м xy мы имеем равную вер-ть обнаружения здесь h высота сосуда. С помощью этого соотнош можно получить барометрич формулу dn(z)-число частиц наход-ся в слое z,z+dz. конццентрация частиц на высоте z. К газу сейчас нельзя применить урав-я Менд- Кл, так как 1) давление газа на разных высотах разное 2) уравн М-К это уравнен состояния свободн газа не наход вне поля. Это уравн можно применить в слое частиц p=nkT -барометрическая формула

13. Реальные газы. Модель слабонеидеального газа. Вычисление конфигурационного интеграла. Модель: 1) молекулы - твердые непроницаемые шарики, массой m, радиусом r. 2)будем считать, что движение происходит по законам класс механ. 3) газ сосредоточен в пределах некот объема. 4) между молек имеется взаимод, котор до сих пор неизвестно в деталях, но глав черты узнаем введя ряд допущений. Если подставим эту энергию в фор-ы статфизики мы не будем знать что с ней делать, поэтому введём ряд положений: взаимод всех молек можно свести к попарным взаимод всех молек, каждой молек со всеми другими. Сумма берется по всем парам частиц. Будем предполагать далее, что энергия попарного взаимод 2х частиц зависит только от расстояния между ними. Для дальнейшего полезно знать сколько можно составить пар, это число выборок по 2 частицы из N возможных. Из математики . Учитывая, что N>>1 мы можем считать число пар  N²/2. Конечно зависимость энергии взаимодействия от расстояния между частиц явл универсальной в том смысле, что для каждой пары она одна и таже. Поэтому мы можем рассмотреть функц W(r)- зависимость потенциальной энергии взаимодейст 2х част от расст между ними. - сила взаимод. При r<r₀ dW/dr<0 поэтому F>0- отталкивание, в обратном случае притяжен. F(r₀)=0 – тч. равновесия (график: ось x-r, y-W, график- кулоновское отталкивание). Нарисованный график нехорош в отношении: на самом деле левая отталкивательная ветвь очень круто идёт вверх, поэтому для многих целей использ упрощ модель, а именно, считают. Что в точке r₀ расположена как бы стенка ближе которой частица подойти не может. Легко сообразить. Что 2 молек рассмотренные как твёрдые непроницаемые шарики не могут сблизиться на расстоян меньше d, поэтому с большой точностью предположим r₀d. В большинстве для электронейтральных атомов и молекул силы взаимодействия быстро убывают с расстоян. Обычно считается. Что они убывают r⁶ поэтому на расст порядка 3-4r₀ W(r)0. Очевидно, что наибольшее значение в тч r₀ . Вытекает основное допущение: будем считать . Физич смысл этого нерав-ва: величина кТ порядка средней кинет энерг дв-я частиц. Поэтому это означает, что потенциальная энергия взаимодейст 2х частиц << Е_к. Стат сумма для газа, конфигурационный инт-л. Мы будем исп-ть квазиклассич выр-е для стат суммы (*). Договоримся в кач-ве коорд мы выберем обычные декарт x_i,y_i,z_i тогда в кач-ве импульсов будут исп-ся обычн проекц имп-ов. Подставив в фор-лу(*)dV=dxdydz, . Как и в случае ид газа инт-е по коорд можно отделить от инт-я по имп-у. Потому что в класс физике энергию всегда можно представить в виде кинетической зависящей только от имп-а и потенциальной зависящей только от коорд. Если бы потенц энергия =0, то инт-л по коорд был бы равен V^N и мы получали бы стат сумму для ид газа -конфигурац инт-л. Такое название от тогою, что подинтегр сумма зависит от конкретного распол-я частиц в пространстве. Используем сведение взаимод к попарному взаимод частиц. Сумма берется по всем парам част. Вместо одного множителя введем функц f(r)+1 или . В силу сделанных предположений о слабой неидеальности газа можно утверждать, что эта вел-на f будет малой. На притягивательной ветви мала, на отталкивательной W и тогда f будет =1. Но если воспользоваться моделью твердого непроницаемого шарика, то эти тч вообще надо исключить из инт-я. Мы их пока оставим ради математ простоты записи, но только чисто формально мы можем заменить произв-е членов. Далее перемножая скобки оставим только члены 0-го и 1-го порядков В данном приближении инт-л от экспоненц ф-ии заменяем суммой инт-ов . Все ф-ии f для каждой пары частиц одинаковы т.е. одинаково зависят от расстояния между 2-я частиц, поэтому в нашей сумме все слагаемые имеют одно и тоже знач-е. Все слагаемые одинаковы и равны инт-лу для 1-й и 2-й част. r- расстояние м/у частицами а  и  задают напр-е прямой от 1-й част ко 2-й. Окончательный конфигурац инт-л:

14. Ур-е сост-я слабонеидеаль-го газа. Сравнение теоритич ур-я сост-ия с ур-ем В-д-В.. Будем нах-ть термическое ур-е: р=р(Т,V,N). Используем: /1/, F= -/2/. Z-статистич. сумма. Найдем lnZ=ln(kZ_ид)=lnZ_ид.+lnk, где Z_ид. – статист сумма для ид. газа, a k=- конфигурационный интеграл. . и . где /*/ - это д.б. при  - оч. малом, -тоже мало) т.е. мы рассматр малую область взаим-я частиц газа (при >r взаимод. мало). Если /*/ выпол-ся, тогда: ( т.к. . Получаем: . подставим получ выраж в /2/: . => . подставим в /1/: - приближенное ур-е сост-я СНИ газа, где . Ее можно расчит в некот приближении. При r<d (диам молек) W(r)= exp=0, а при r>d и . В рез-те имеем , где V₀ – объем 1-ой частицы, а J’= если разделить на V, то получим средн энерг взаимод 2-х частиц. . Т.е. . Тогда термическое ур-е: . Из ур-я видно, что p в СНИ газа зависит от T,V,N. Ур-е сост-я реаль-х газов, предлож-е В-д-В где точнее опис-ет св-ва газов, чем ур-е Мен-Кл. Чтобы мож было сравнить теорит ур-е и ур-е В-д-В необходимо . . т.к. и R = kN_A то . Теорит ур-е имеет след вид . Область применим.: теорит ур-е применимо только к СНИ газу, ур-е ,В-д-В - к любому газу. => необходимо уменьшить обл его применимости. Если т.е газ достаточно разрежен. Тогда . => Ур-е ВдВ . Теперь ур-я в одинаковой форме и их мож сравнить: 1-ый член одинаков, поправка b учитывает собственный объем молекул - учетверенн объем всех молекул, если взять 1 моль газа. Далее где - число пар молекул в одном моле. *число пар – полная энерг взаимод-я в данном молярном объеме. , тогда -не зависит от объема, она связ-а с энер взаимод-я частиц. Поправка а – поправка на энергию взаим (знак – означ то, что энер взаим отриц). Оба ур-я: теорит и ВдВ-дают одинаков рез-ты для СНИ, при этом выясняется точный физ смысл пост a и b в ур-ии ВдВ. Ур-е ВдВ полуэмпирич ур-е и составл след образом: 1)берется ур-е для идеаль газа pV=RT. Идеаль газ можно сжать до точки. Реаль газ нельзя сжать до точки, т.к. есть предел связ-ый с собственн объемом молекул и обязательно > его. Значит газ мож расшир и сжимат в определ пределе. Поэтому этот объм необх вычесть из объема газа p(V-b)=RT; 2)2-ая поправка учит след обр (рис: 2-е окруж одна впис в др впис изобр шире, молек в виде точек у внутр сторон опис окруж: от одной стрелка внутрь всех окр) если молекула нах-я у стенки, то она притягив. другими молек во внутрь. Выдел-т 2-а слоя пристеноч и след за пристеноч. Притяжение обуслав дейс-ем этих 2-х слоев. Сила взимодействия б. ~ числу молекул в слоях , точнее (но n₁=n₂) , поэтому и была внесена поправка a/V²: . Ур-е ВдВ простое в матем-ом отношении, учитыв глав особенн неидеаль газа: отталкив на малых расстоя-х, притяжение на >. Его конструкция такова, что оно дает верные рез-ты не только для газа: горячего и разряженного (СНИ), но и для холодного и плотного газа. Ур-е ВдВ допускает экстраполяцию на жид сост-я в-ва., но уже работает неточно. Сходство с жид-тью связано с отталкив-м мол-л на близких расст-х – с поправкой b. Физ смысл пост a и b, кот был придан при сравнении ур-ия ВдВ с теоритич ур-м, оправдан только для слабонеидеаль газа, для сильнонеид газа и жид-ти толковать так смысл поправок нельзя – это просто const-ы, чьи значения подбираются так, чтобы ур-е согласовывалось с эксперим данными.

15. Теорема о равномер-м распр-ии энергии сс. Док-во ее. Каждому квадратич-му слагаемому в среднем можно сопоставить одну и ту же эн-ю . - внутр эн системы. Для нахожд-я внутр эн-ии надо знать сколько квадратичных слагаемых входит в выражение эн-ии. - к поступательн движ.; -к вращат-му; - к колебат движ. Наиболее часто , , 2N –для 2-атомных, 3N –для 3-атомных; Известно, что Применим эти ф-лы к 4-м случаям: 1. одноат-ый газ - , 2. 2-атомн идеал газ с жесткой связью - , 3. 2-атомн ид газ с нежесткой связью м/у молек-ми - , 4. кристал реш-ка - , Помимо рассчета теплоем-тей из теоремы о равном-ом распред-ии эн-ии по степеням свободы след-т важный вывод: кТ м.б. взята за меру интенсивности внутр движ-ия в классич системе. Понятие кинетич-й температуре. Это верно, если расс-ть 1-атомн-й ид газ. Если газ нах-ся в равновесии и состоит из легких и тяжелых частиц, то мы можем найти отнош-ие скоростей тех и др частиц. и . Док-во: Пусть имеется равновесн сс, имеющая тем-ру Т и эта сс такая, что эн-ю ее м. пред-ть в виде суммы квадратичных членов 1. 2. cc равновесна, тем-ра Т. К такой сс применимо канонич-е распред-е: По правилу вычисл-я средних любой величины: Подинтегральная ф-ия будет такая, что многократный инт-л можно разложить на произвед-е отд-х инт-ов. Без ущерба для точности пределы интегр-ия в каждом инт-ле м. положить равными , хотя на самом деле пределы конечны, но замена ошибки не вносит, т.к. величина -энергия, связан-я с какой-то степенью свободы, ее max это энергия всей сс вместе взятой, она равна , тогда кажд сомножитель м. вычислить независимо, тогда инт-лы почти все сократятся и ост-ся: Из мат-ки: ,где => . Некот физ сист, где энерг м/б представлена в виде суммы квадратич-х слагаем-х. 1) 1-атомный идеаль газ: энерг сист , пременные р_хi, p_yi, p_zi – всего 3N. Тогда теорема запишется след образом , т.е. теорема о равномерном распределении энерг по степеням свободлы применима.