7. Асимптоты.

Предложение. Прямые являются вертикальными асимптотами функции .

Доказательство. Найдем односторонние пределы функции в точке 0:

, .

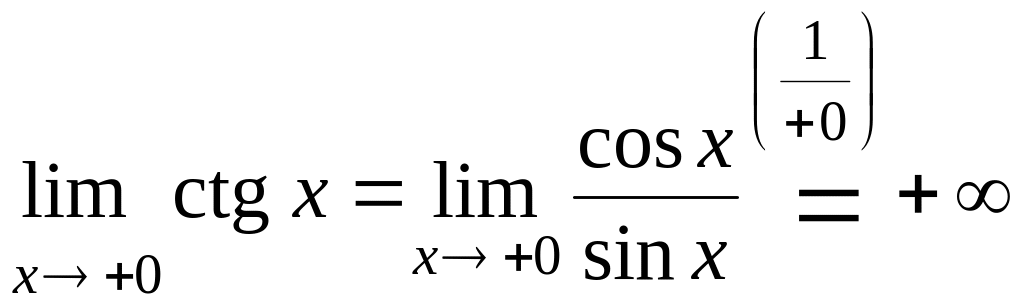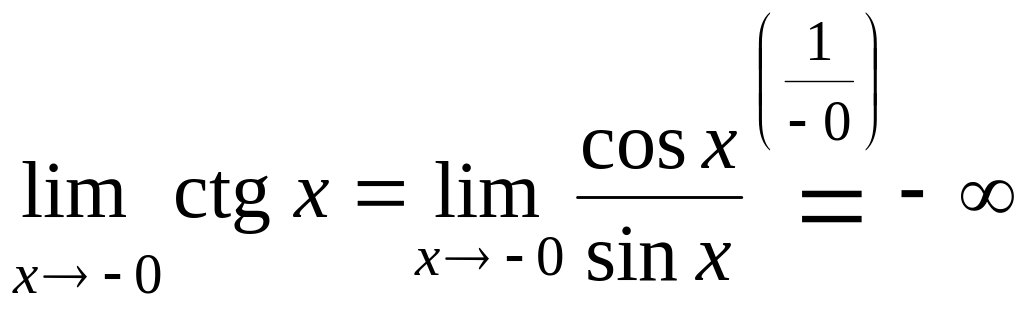В силу периодичности функции тангенс заключаем, что в точках , ее односторонние пределы равны бесконечности. Предложение доказано.

8. Множество значений.

Предложение. Множеством значений функции является множество всех действительных чисел.

Доказательство. Число 0 является значением функции котангенс, так как . Докажем, что все числа, не равные нулю, также являются значениями функции .

Возьмем произвольное действительное число . Так как множеством значений тангенса является множество всех действительных чисел и , то существует точка х₀, для которой . Тогда , т. е. . Следовательно, .

9. График функции .

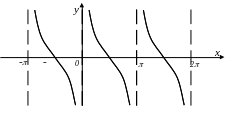
Обратные тригонометрические функции

§ 24. Функция и ее свойства

Функция строго возрастает на отрезке , поэтому ее сужение на этот отрезок является обратимой функцией.

Определение. Функция, обратная для сужения функции на отрезок , называется арксинусом и обозначается .

Из определения обратной функции следует:

.

1. Область определения, множество значений. Из определения обратной функции следует, что областью определения и множеством значений функции является соответственно множество значений и область определения функции , где . Таким образом, , .

2. Ограниченность. Функция ограничена, так как ее множество значений является ограниченным числовым множеством. Таким образом, для любого х .

3. Непрерывность. Функция непрерывна как обратная для непрерывной функции.

4. Четность, нечетность.

Предложение. Функция является нечетной.

Доказательство. Область определения арксинуса – симметричное относительно нуля множество.

Возьмем произвольную точку и докажем равенство . Пусть . По определению арксинуса имеем и . Тогда и в силу нечетности синуса . По определению арксинуса получаем . Из равенств и следует . Предложение доказано.

5. Монотонность. Функция является обратной для строго возрастающей функции, следовательно, также строго возрастает.

6. Нули и промежутки знакопостоянства.

Для того, чтобы найти нули функции, решим уравнение:

Так как и функция строго возрастает на своей области определения , то при и при .

7. График функции .

Графики функций , , и симметричны относительно прямой , как графики взаимно-обратных функций.

§ 25. Функция и ее свойства

Функция строго убывает на отрезке , поэтому ее сужение на этот отрезок является обратимой функцией.

Определение. Функция, обратная для сужения функции на отрезок , называется арккосинусом и обозначается .

Из определения обратной функции следует:

.

1. Область определения, множество значений. Из определения обратной функции следует, что областью определения и множеством значений функции является соответственно множество значений и область определения функции , где . Таким образом, , .

2. Ограниченность. Функция ограничена, так как ее множество значений является ограниченным числовым множеством. Таким образом, для любого х[–1, 1].

3. Непрерывность. Функция непрерывна как обратная для непрерывной функции.

4. Четность, нечетность. Докажем, что функция не является ни четной, ни нечетной. Возьмем симметричные относительно нуля точки из области определения арккосинуса, например, 1 и -1. Значения функции в этих точках и не равны и не являются противоположными по знаку. Это и означает, что функция не удовлетворяет определениям ни четной, ни нечетной функции.

5. Монотонность. Функция является обратной для строго убывающей функции, следовательно, также строго убывает.