§ 22. Функция и ее свойства
Определение.
Тангенсом
действительного числа
называется число
.
Функция
является частным функций
и
.
Поэтому ее свойства вытекают из свойств
этих функций.
1.
Область
определения.
Так как значение
определено
для любого числа x,
при котором
,
то Df = R\{
}.
2. Периодичность.
Предложение.
Функция
является периодической с основным
периодом
.
Доказательство.
Так как
Df = R\{
},
то никакое положительное число, меньшее
,
периодом функции
не
является.
Осталось
показать, что
–
период:
.
Предложение доказано.
3. Нули функции, промежутки знакопостоянства.
.
Если
,
то
.
Следовательно,
.
Если
,
то
.
Следовательно,
.
Учитывая периодичность функции тангенс, получаем:
,
.
4. Четность, нечетность.
Предложение. Функция является нечетной.
Доказательство. Область определения функции является симметричным относительно нуля множеством и
для любого
.
Следовательно, функция тангенс – нечетная.
5. Монотонность.
Предложение.
Функция
строго возрастает на интервалах
.
Доказательство.
Опираясь на свойство периодичности,
достаточно доказать, что функция
строго возрастает на
.
Возьмем произвольные
точки
и
,
такие что
.
Рассмотрим разность значений функции
в этих точках
.
Поскольку
и
,
то
и
.
Следовательно,
,
т.е.
.
Тем самым доказано, что функция
строго возрастает на
интервале
.
6. Непрерывность. Функция непрерывна на своей области определения как частное непрерывных функций.
7. Асимптоты.
Предложение.
Прямые
,
являются вертикальными асимптотами
функции
.
Доказательство. Найдем односторонние пределы функции в точке :
,
.
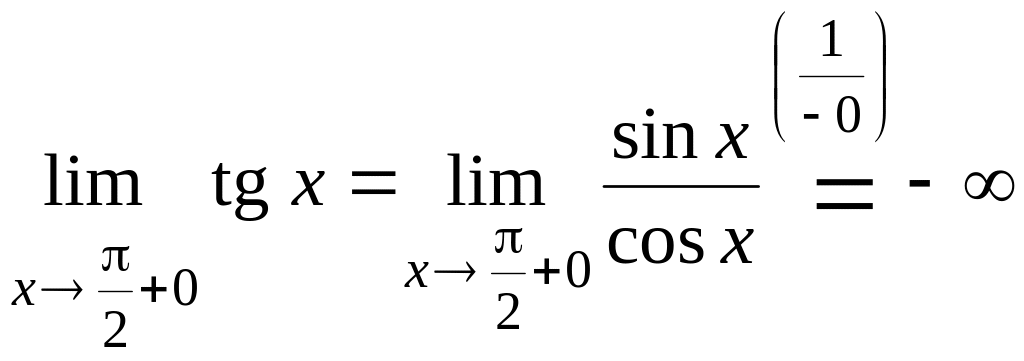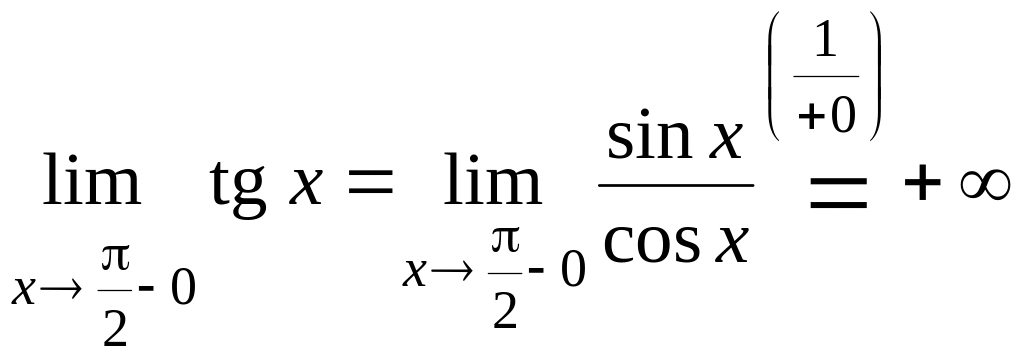Из периодичности
тангенса следует, что во всех точках
,
ее
односторонние
пределы равны бесконечности. Предложение
доказано.
8. Множество значений.
Предложение. Множеством значений функции является множество всех действительных чисел.
Доказательство. Достаточно доказать, что на интервале функция тангенс принимает все действительные значения.
Пусть r
– произвольное
действительное число. Так как
и
,
то существуют точки х1
и х2
(х1
< х2),
для которых
.
Из непрерывности функции на R
следует, что она непрерывна на отрезке
.
По теореме Больцано-Коши о промежуточных
значениях непрерывной на отрезке функции
заключаем, что число r
является значением функции в некоторой
точке отрезка
,
т. е.
.
Следовательно,
.
9. График функции называется тангенсоидой.
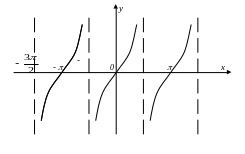
§ 23. Функция и ее свойства
Определение.
Котангенсом
действительного числа
называется число
.
Функция
является частным функций
и
.
Поэтому ее свойства следуют из свойств
этих функций. Кроме того,
для всех
1.
Область
определения.
Так как значение
определено
для любого числа x,
при котором
,
то Df = R\{
}.
2. Периодичность.
Предложение.
Функция
является периодической с основным
периодом
.
Доказательство. Так как Df=R\{ }, то никакое положительное число, меньшее , периодом функции не является. Осталось показать, что число – период:
.
3. Нули функции, промежутки знакопостоянства.
Найдем
нули функции, для этого решим уравнение:
.
Из
тождества
(
)
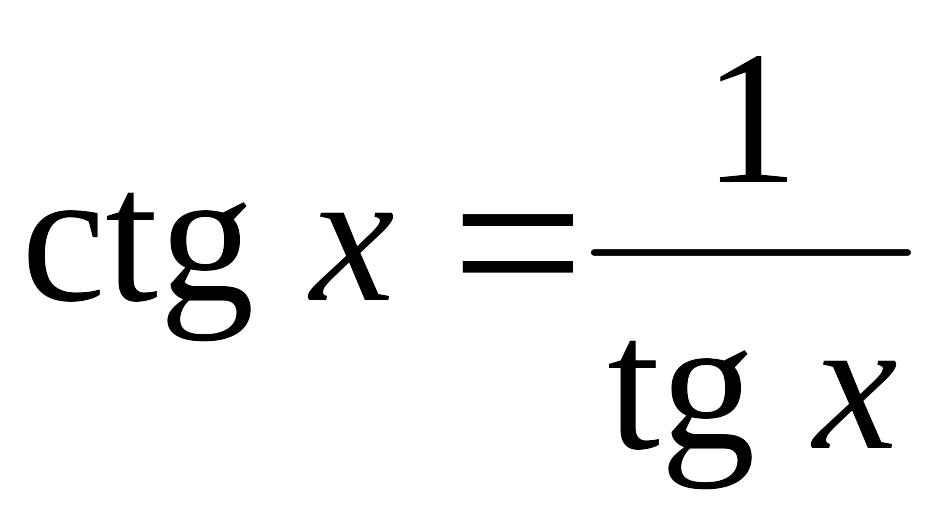следует, что функции тангенс и котангенс
при
принимают одинаковые по знаку значения.
Следовательно,
,
.
4. Четность, нечетность.
Предложение. Функция является нечетной.
Доказательство. Область определения функции является симметричным относительно нуля множеством и
для любого
.
Следовательно, функция котангенс – нечетная.
5. Монотонность.
Предложение.
Функция
строго убывает на интервалах
.
Доказательство.
Опираясь на свойство периодичности,
достаточно доказать, что функция
строго убывает на
.
Возьмем произвольные
точки
и
,
такие что
.
Рассмотрим разность значений функции
в этих точках
.
Поскольку
и
,
то
и
.
Следовательно,
,
т.е.
.
Тем самым доказано, что функция
строго убывает на
.
6. Непрерывность. Функция непрерывна на своей области определения как частное непрерывных функций.