§6. Классификация элементарных функций

К основным элементарным функциям относятся следующие функции:

• степенная 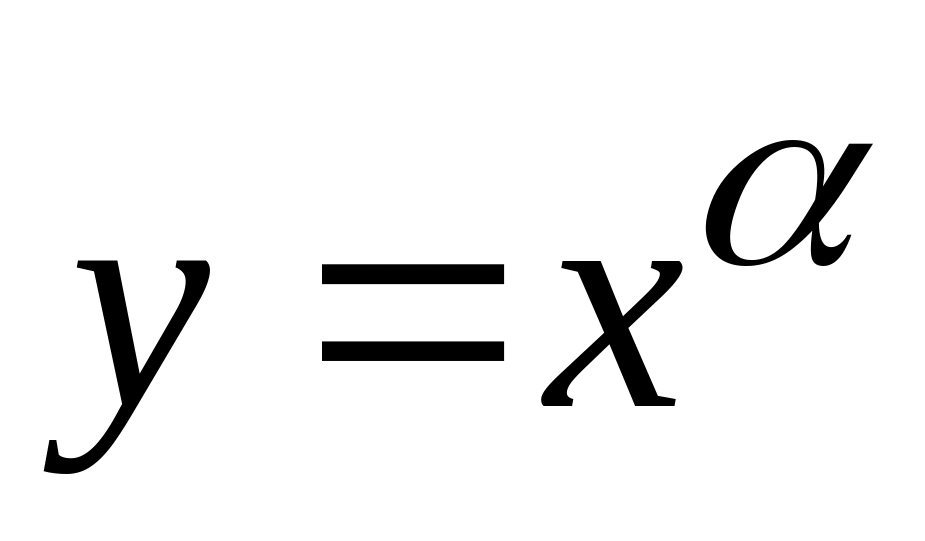( 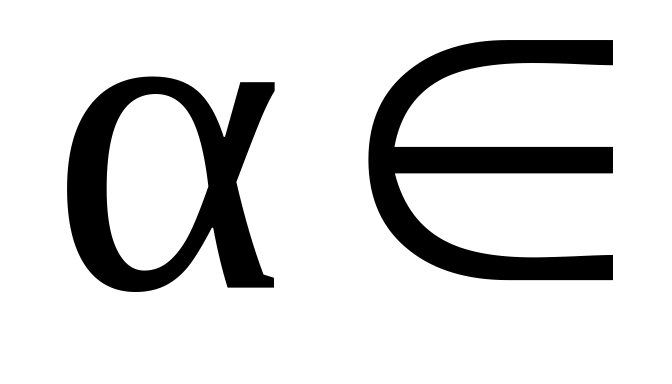R, ;

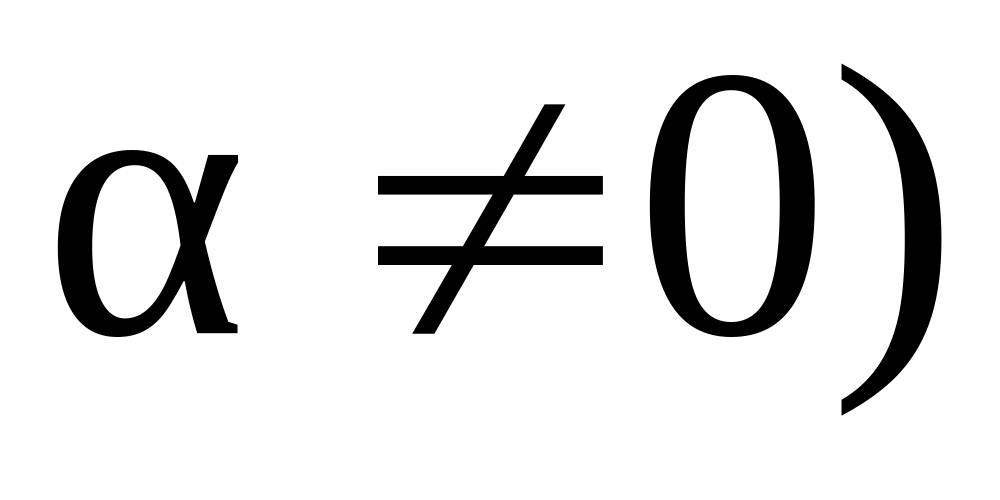• показательная ;

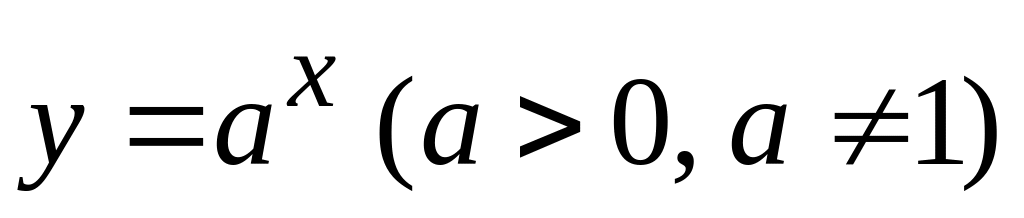• логарифмическая ;

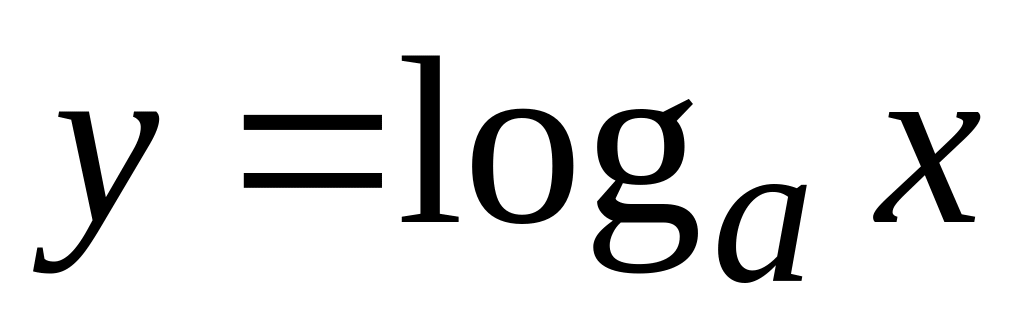
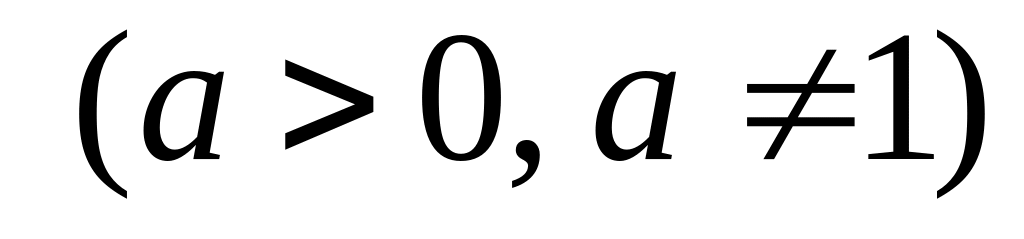• тригонометрические

;

• обратные тригонометрические ;

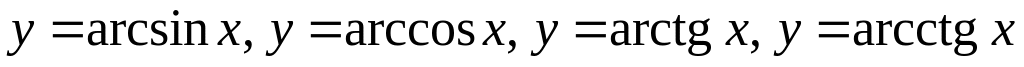Определение. Элементарной называется функция , полученная из основных элементарных функций и функций (с – число) с помощью конечного числа арифметических операций и композиций.

Примеры. – элементарная функция. Функции не являются элементарными.

Определение. Многочленом п-ой степени называется функция вида , где – числа, , п – неотрицательное целое число.

Примеры. – многочлен 5-ой степени, – многочлен нулевой степени

Определение. Рациональной функцией называется частное двух многочленов.

Пример. – рациональная функция.

Многочлен является частным случаем рациональной функции.

Определение. Функция называется алгебраической, если она получена из функций и y = c (c – произвольное число) с помощью конечного числа арифметических операций, взятия корней натуральной степени и композиции функций.

Например, рациональные функции являются алгебраическими.

Определение. Алгебраическая функция , не являющаяся рациональной, называется иррациональной.

Пример. – иррациональная функция.

Определение. Функция , не являющаяся алгебраической, называется трансцендентной.

К трансцендентным функциям, например, относятся все тригонометрические, обратные тригонометрические, показательная и логарифмическая функции.

Классификацию элементарных функций можно представить следующей схемой.

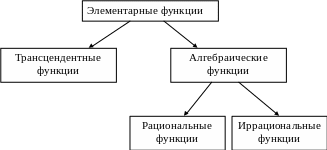
Глава 2. Элементарные функции и их свойства

§ 7. Степенная функция с натуральным показателем

Определение. Степенью действительного числа a с натуральным показателем n называется число, равное произведению n сомножителей, каждый из которых равен a:

.

Свойства степени с натуральным показателем

Доказательство этих свойств следует непосредственно из определения степени с натуральным показателем.

Определение. Степенной функцией с натуральным показателем называется функция, определенная формулой ( , n  1).

Замечание. Функцию является линейной, ее не относят к степенным. Однако в доказательствах мы не будем исключать этот случай.

Свойства функции ,

1. Область определения. , поскольку операция возведения в натуральную степень определена для любого действительного числа.

2. Нули функции, промежутки знакопостоянства. Очевидно, . Если n четно, то для любого . Если n нечетно, то для всех и для всех

3. Непрерывность. Функция непрерывна на R как произведение n экземпляров функции , непрерывность которой в любой точке числовой прямой легко устанавливается непосредственно по определению.

4. Четность, нечетность.

Предложение. Функция , является четной, если n четно, и нечетной, если n нечетно.

Доказательство. – симметричное относительно нуля множество.

Пусть , .

Тогда для любого . Следовательно, – четная функция при четном п.

Пусть , .

Тогда для любого . Следовательно, – нечетная функция при нечетном п.