6. Нули и промежутки знакопостоянства.

Так как , то . Функция строго убывает, поэтому при .

7. График функции .

Графики функций , , и симметричны относительно прямой , как графики взаимно-обратных функций.

§ 26. Функция и ее свойства

Функция строго возрастает на интервале , поэтому ее сужение на этот интервал является обратимой функцией.

Определение. Функция, обратная для сужения функции на интервал , называется арктангенсом и обозначается .

Из определения обратной функции следует:

.

1. Область определения, множество значений. Из определения обратной функции следует, что областью определения и множеством значений функции является соответственно множество значений и область определения функции , где . Таким образом, , .

2. Ограниченность. Функция ограничена, так как ее множество значений 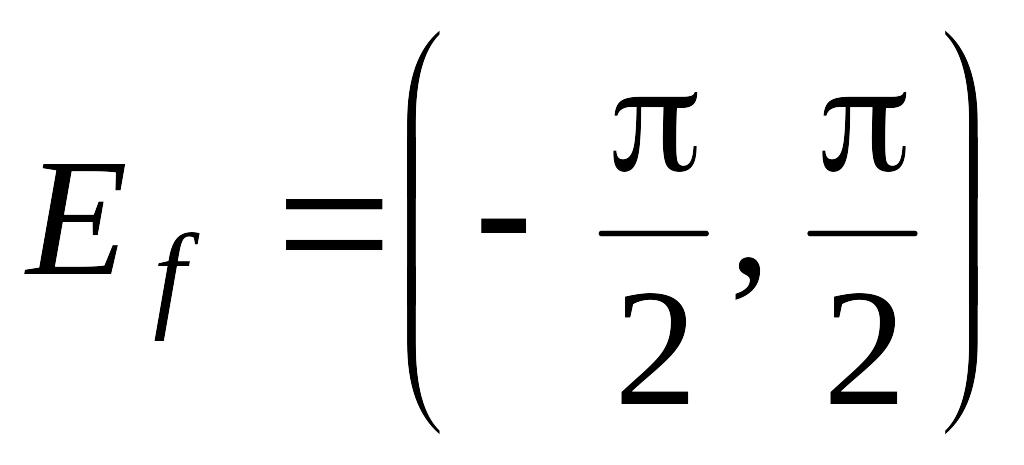является ограниченным числовым множеством. Таким образом, для любого действительного х.

3. Непрерывность. Функция непрерывна как обратная для непрерывной функции.

4. Четность, нечетность.

Предложение. Функция является нечетной.

Доказательство. Область определения арктангенса – симметричное относительно нуля множество.

Проверим выполнимость равенства . Возьмем произвольную точку и докажем равенство . Пусть . По определению арктангенса и . Тогда и в силу нечетности тангенса . По определению арктангенса имеем: . Из равенств и получаем .

5. Монотонность. Функция является обратной для строго возрастающей функции, следовательно, также строго возрастает на своей области определения.

6. Нули и промежутки знакопостоянства.

Для того, чтобы найти нули функции, решим уравнение:

Так как и функция строго возрастает на R, то при и при .

7. Горизонтальные асимптоты.

Предложение. Прямые и являются горизонтальными асимптотами функции на + и – соответственно.

Доказательство. В силу нечетности арктангенса достаточно доказать, что . Напишем определение предела:

Для произвольного возьмем . Тогда для любого в силу строгого возрастания функции из неравенства следует . Так как , то . Из последних двух неравенств получаем , что означает: . Тем самым доказано, что .

8. График функции .

Графики функций , x(-/2, /2), и симметричны относительно прямой , как графики взаимно-обратных функций.

§ 27. Функция и ее свойства

Функция строго убывает на интервале , поэтому ее сужение на этот промежуток является обратимой функцией.

Определение. Функция, обратная для сужения функции на интервал , называется арккотангенсом и обозначается .

Из определения обратной функции следует:

.

1. Область определения, множество значений. Из определения обратной функции следует, что областью определения и множеством значений функции является соответственно множество значений и область определения функции , где . Таким образом, , .

2. Ограниченность. Функция ограничена, так как ее множество значений является ограниченным числовым множеством. Таким образом, для любого действительного х.

3. Непрерывность. Функция непрерывна как обратная для непрерывной функции.

4. Четность, нечетность. Докажем, что функция не является ни четной, ни нечетной. Возьмем симметричные относительно нуля точки, например, 1 и –1. Значения функции в этих точках и не равны и не являются противоположными по знаку. Это и означает, что функция не удовлетворяет определениям ни четной, ни нечетной функции.

5. Монотонность. Функция является обратной для строго убывающей функции, следовательно, также строго убывает.