§3. Способы задания функций
Функция считается заданной, если указаны ее область определения и закон соответствия.
I. Аналитический способ.
Указывается формула
вида
,
где
– некоторое аналитическое выражение,
содержащее переменную х.
В этом случае областью определения
функции f
является
такое множество Х,
во всех точках которого значение функции
может быть вычислено по указанной
формуле.
Пример.
Функция
.
Областью определения
является множество
.
Во всех точках
соответствие устанавливается по закону:
.
II. Описательный способ.
Закон соответствия устанавливается с помощью словесной формулировки.
Примеры.
1. На
множестве натуральных чисел определим
функцию f,
полагая
– сумма цифр натурального числа х.
Например,
,
.
Следующие функции играют важную роль в математическом анализе, поэтому для них введены специальные обозначения.
2.
Функция
– «Целая часть числа» (антье от х).
Определение.
Целой
частью
действительного
числа х
называется наибольшее целое число
,
не превосходящее х.
3.
Функция
– «Дробная часть числа».
Определение.
Дробной
частью
действительного
числа х
называется число
.
Например,
.
4.
Функция
– «Зн
ак
числа» (сигнум от х).
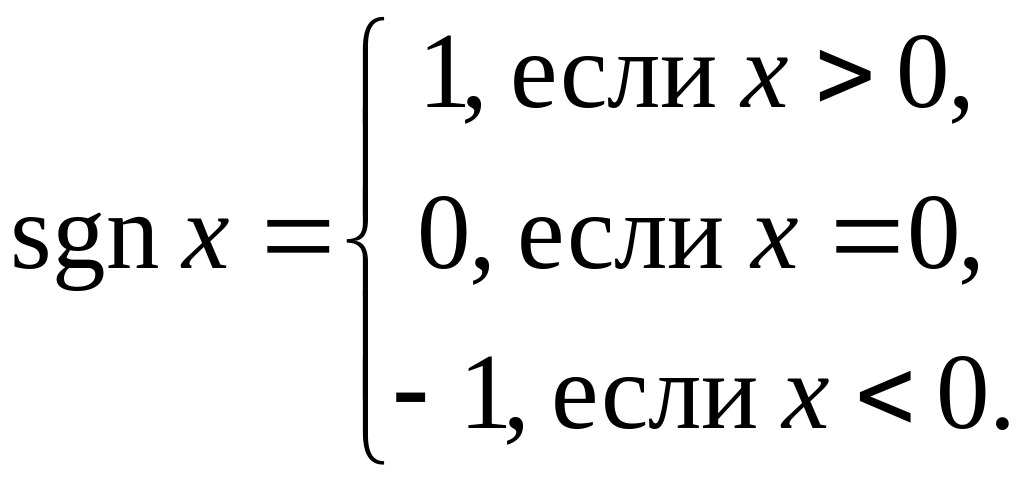
5. Функция Дирихле.
Замечание. Функции, рассмотренные в примерах 2-5, не являются элементарными (определение элементарной функции дано ниже).
III. Табличный способ.
П
Х
1
2
3
4
У
-2
0
5
1
.
Функция f:
Х → Y
задана таблицей:
В этом случае
,
,
,
.
IV. Графический способ.
На координатной
плоскости построим кривую (множество
точек), обладающую свойством: любая
вертикальная прямая пересекает ее не
более чем в одной точке. Такая кривая
задает функцию f,
областью определения Df
которой служит проекция этой кривой
на ось ОХ,
а значения в точках
Df
определяются как ординаты соответствующих
точек на кривой.
Этот способ часто применяется при иллюстрации понятий и теорем математического анализа.
§4. Операции над функциями
Определение. Суммой функций f и g называется функция f+g, область определения и закон соответствия которой определяются следующим образом:
1)
;
2)
для всех
.
Определение. Произведением функций f и g называется функция fg, для которой:
1)
;
2)
для всех
.
Определение.
Частным
функций f
и
g
называется
функция
,
для которой:
1)
;
2)
для всех
.
Пример. Найдем
область
определения функции
.
Данная функция
является частным функций
и
.
По определению частного двух функций
ее область определения состоит из тех
значений х,
для которых выполнены три условия:
,
и
.
Получаем систему:
.
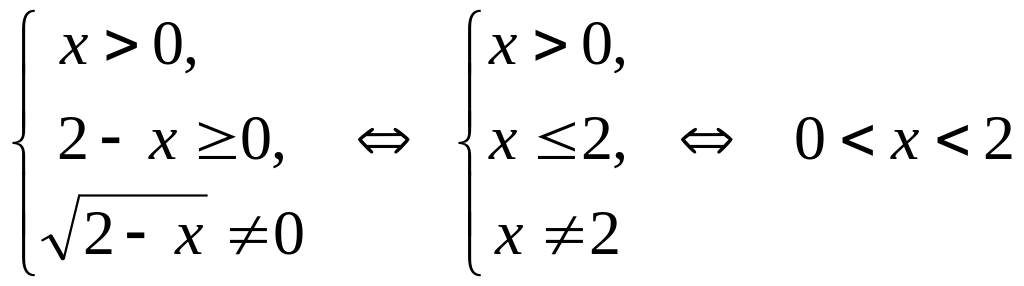Таким образом,
областью определения данной функции
является множество
.
Определение.
Композицией
функций f
и
g
называется
функция
,
для которой:
1)
;
2)
для всех
.
Пример. Для
функций
и
найдем композиции
и
и их области определения.
1. По определению
композиции функций f
и
g
область
определения функции
состоит из тех значений х,
для которых выполнены два условия:
и
.
Получаем систему:
.
Таким образом,
областью определения композиции
является множество
.
Значения функции
во всех точках множества
находятся по формуле:
.
2. Для функции
область определения находим, исходя из
условий
и
.
Получаем систему:
.
Получили:
.
Во всех точках области определения
значения функции
вычисляются по формуле:
.
Заметим, что функции и не равны. Это следует хотя бы из того, что полученные функции имеют разные области определения.
Вывод. Операция композиции функций не коммутативна.
Определение.
Сужением
функций f
на множество
называется
функция
,
для которой:
1)
;
2)
для всех
.
Пример. Рассмотрим функции f и g, заданные одной формулой, но на разных множествах:
Функция g является сужением функции f на множество [0,+): g= f|[0,+).
Определение.
Пусть функция f
инъективна.
Обратной функцией для
функции f
называется функция
,
область определения и закон соответствия
которой определяются следующим образом:
1)
;
2)
для всех
.
Определение. Функция называется обратимой, если она имеет обратную функцию.
Очевидно, функция обратима в том и только в том случае, когда она каждое свое значение принимает ровно один раз.
Замечание. Так
как точки (х, у)
и (у, х)
симметричны относительно прямой у=х,
то графики числовых функций f
и
симметричны относительно биссектрисы
I
и III
координатных углов.
Пример.
Рассмотрим функцию
.
Каждое свое значение она принимает
ровно один раз, следовательно, обратима.
Найдем обратную для нее функцию
.
Для этого из равенства
выразим переменную х.
Получим:
.
Таким образом, обратная функция каждому
значению y
ставит в соответствие число
.
Переобозначив переменную, получаем:
.
