§ 14. Свойства степенной функции с рациональным показателем, связанные с неравенствами
Предложение 1.
Если
,
то
на
и
на
для любых рациональных r
и q.
Доказательство.
Если
,
то
.
По свойству степенной функции с
положительным рациональным показателем
(предложение 10, (1)) на интервале
выполняется неравенство
.
Умножая обе его части на хq,
получаем
.
Для интервала
рассуждения аналогичны.
Предложение 2. Функция , , на принимает только положительные значения.
Доказательство следует из свойств функции при r 0 и r < 0, рассмотренных в п. 5 § 12 и п. 5 §13.
§ 15. Определение степени действительного числа с иррациональным показателем
Прежде чем дать определение степени действительного числа с произвольным действительным показателем и обосновать его корректность, проведем некоторые вспомогательные рассуждения.
Неравенство
Бернулли:
для любых
действительного
и натурального
п.
Доказательство. Применим метод математической индукции. При п = 1 неравенство очевидно выполняется. Предположим, что оно выполняется при п и осуществим индуктивный переход:
.
На основании ММИ заключаем, что неравенство справедливо при любом натуральном п.
Лемма.
при любом
действительном
.
Доказательство. Требуется доказать:
.
Рассмотрим случай
.
Обозначим
.
По неравенству Бернулли получаем:
для любого
.
Отсюда
(*).
Для произвольного
рассмотрим неравенство
.
Возьмем натуральное
число N,
удовлетворяющее неравенству
(такое N
существует, так как множество натуральных
чисел неограниченно сверху). Тогда для
всех натуральных
будет выполнено
,
отсюда
,
и в силу неравенства (*) имеем:
.
Следовательно,
.
Рассмотрим случай
.
Тогда
.
По доказанному выше
.
Используя свойства степеней, имеем:
Предложение.
при любом
действительном
.
Доказательство. При а = 1 утверждение очевидно.
Рассмотрим случай
.
Требуется доказать:
.
Возьмем произвольное
.
Поскольку
по лемме 13 и
,
то все члены
последовательностей
и
с номерами, большими некоторого
,
принадлежат интервалу
.
Пусть
.
Возьмем произвольное рациональное r,
удовлетворяющее неравенству
.
Очевидно,
,
поэтому найдется такое натуральное п,
для которого будет выполнено:
.
Тогда по свойству степенной функции с
рациональным показателем (предложение
1, § 14) имеем:
и
.
Поскольку п-ый
и (п+1)-ый
члены последовательностей
и
при
принадлежат интервалу
,
то
,
т. е.
.
Следовательно,
.
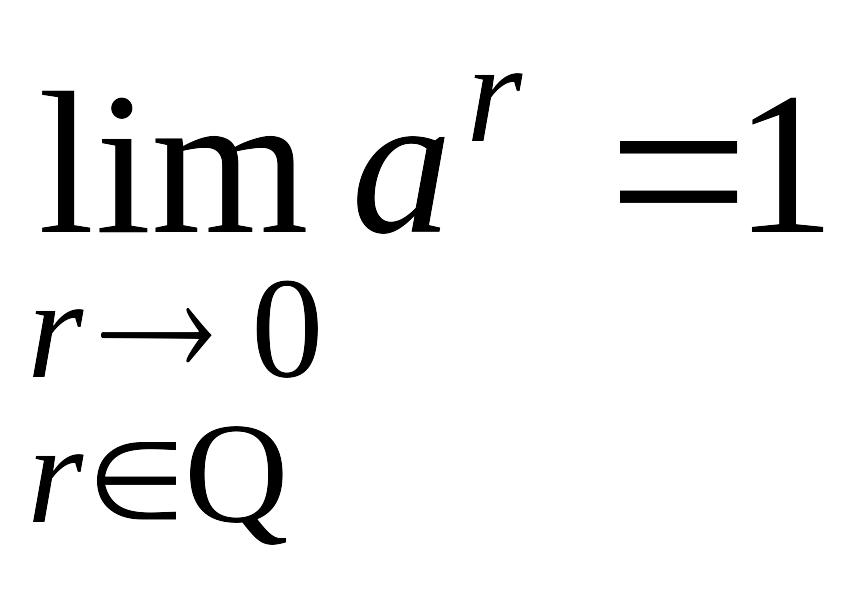Рассмотрим случай
.
Тогда
и
по доказанному выше. Используя свойства
степеней, имеем:
.
Определение.
Степенью
действительного числа
с иррациональным показателем
называется число
,
где
– произвольная последовательность
рациональных чисел, сходящаяся к .
Корректность определения
Рассмотрим случай
(при
рассуждения аналогичны).
Существование.
Пусть
– некоторая строго возрастающая
последовательность рациональных чисел,
сходящаяся к
(например, последовательность десятичных
приближений числа
по недостатку), и q
– некоторое
рациональное число, большее
(например,
).
Поскольку
и
,
то по свойству степени с рациональным
показателем (предложение 11)
и
при любом
.
Таким образом, последовательность
строго возрастает и ограничена сверху,
следовательно, имеет конечный предел.
Обозначим
.
Единственность.
Пусть
– произвольная последовательность
рациональных чисел, сходящаяся к .
Докажем, что
.
Поскольку по условию
,
то
.
Так как
,
то
по доказанному выше предложению. Тогда
по свойствам степени с рациональным
показателем получаем:
.
Замечания. 1. Если
r
является
рациональным числом, то
для любой последовательности
рациональных чисел, сходящейся к r
(a > 0).
Таким образом, значение предела
совпадает с ранее введенным значением
степени
с
рациональным показателем.
2. Если
a < 0,
то степень
с иррациональным показателем
не определена. Например, рассмотрим
выражение
.
Возьмем последовательность
рациональных чисел, сходящуюся к
.
Зададим ее так, чтобы среди ее членов
было бесконечно много несократимых
дробей r=
каждого из следующих видов: 1) k
– нечетно, m
– нечетно,
тогда
;
2) k
– четно, m
– нечетно,
тогда
;
3) k
– четно, m
– четно,
тогда значение
не определено. Очевидно, последовательность
не имеет предела, следовательно, значение
не определено.
3. При определении степени аa положительного числа а с иррациональным показателем a можно рассматривать класс только возрастающих (убывающих) последовательностей рациональных чисел, сходящихся к a.
4. Существуют и другие подходы к определению степени аa (a > 0, I). В основе этих подходов лежат следующие понятия.
2) Предел по
множеству:
.
3) Точные грани
числового множества: если
,
то
=
;
если
,
то
=
,
4) Разделяющее
число: если
,
то
(
);
если
,
то
(
).