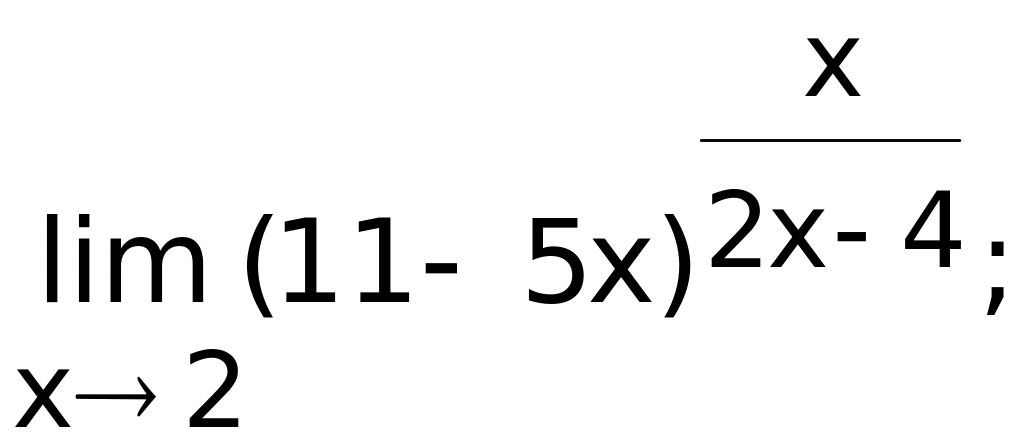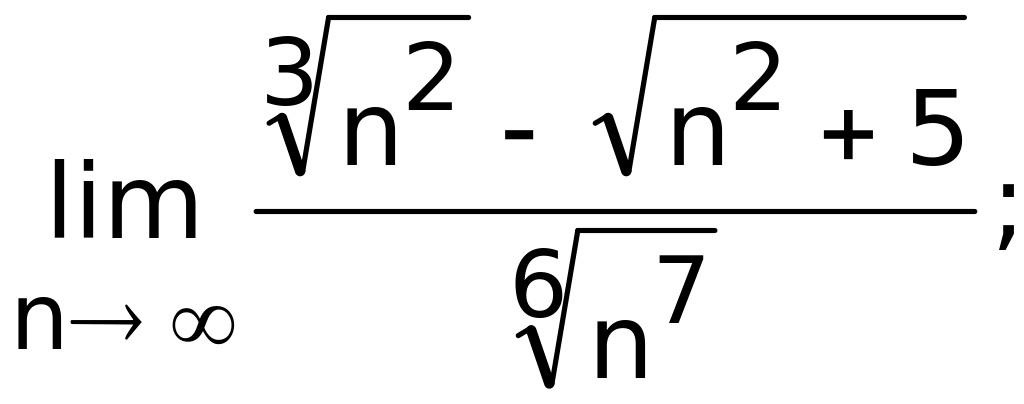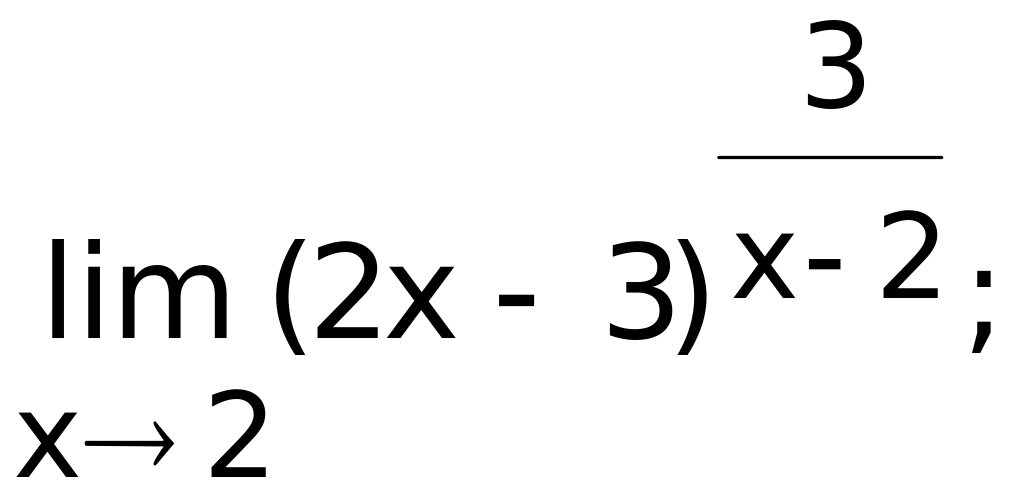2. Преобразования графиков функций.

При построении графиков функций применяют такие приемы, как построение "по точкам", действия с графиками (сложение, вычитание умножение графиков) и преобра-зования графиков (сдвиг, растяжение).

Отправляясь от графика функции y=f(x), можно по-строить графики следующих функций:

1. y=f(x-a) - первоначальный график, сдвинутый

вдоль оси ОХ на величину а.

2. y=f(x)+b - тот же график, сдвинутый вдоль оси

ОУ на величину b.

3. y=Af(x) - исходный график, растянутый вдоль

îñè ÎÓ â À ðàç.

4. y=f(kx) - тот же график, растянутый вдоль оси

ÎÕ â 1/k ðàç.

Таким образом, по графику функции y=f(x) можно по-строить график функции вида y=Af(k(x-a))-b.

Пример. Построить график функции y=2ln((0.5x+0.5)+1.

Решение. Представим нашу функцию в следующем виде y=2ln((x+1)/2)+1. Здесь А=2, k=1/2, а=-11/2, b=-1.

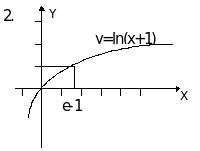
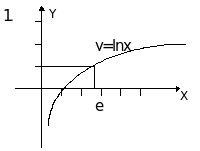
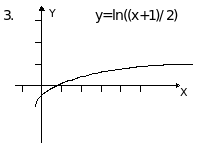
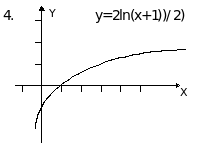
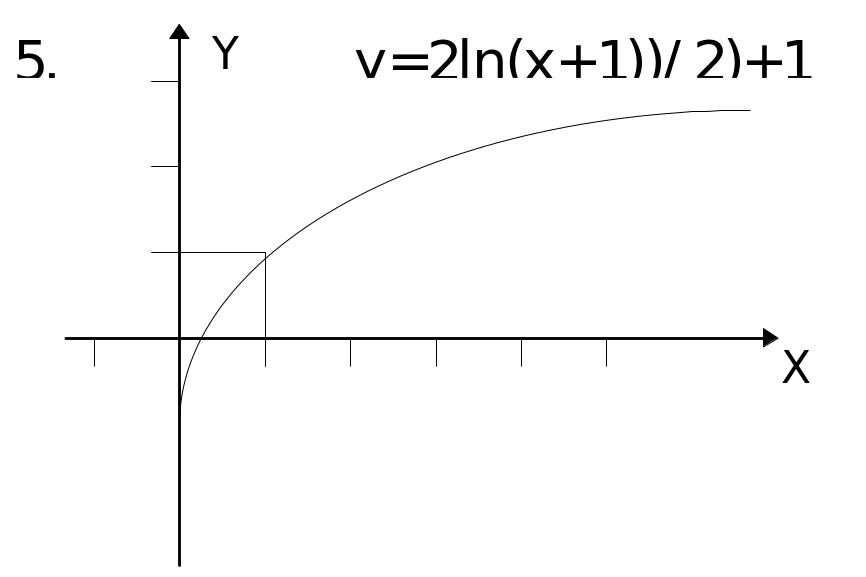
В качестве исходного возьмем график функ-ции y=lnx. Затем строим график функции y=ln(x+1), сдвигая график функции y=lnx вдоль оси ОХ на одну единицу влево. Затем строим график функции у=ln(x+1)/2, растягивая предыдущий график вдоль оси ОХ в два раза. Далее, растягивая последний график вдоль оси ОУ в два раза, получим график функции y=2ln((x+1)/2). Наконец, сдви-гая последний график на одну единицу вверх вдоль оси ОУ, получим требуемый график.

Задача 9. Построить график функции y=Af(kx+b)+B, деформацией и сдвигом графика функции y=f(x).

N	Функции	N	Функции
1	2y+4+sin2x=0; y= ;	6	y-2+2tg3x=0; y=-3x-2+3,5;
2	y=cos2x-3; y=-lg(x+4)+2;	7	2y-2-3cos2x=0; y=2x-3-3,2;
3	y-2=2tg(x/3); y+2+log2(x-2)=0;	8	2y-4+sin2x=0; y=5-lg(x+4);
4	y=-5cos(3x+2)-1; y-1-31-x=0;	9	2y+2+cos2x=0; y=2x-2+2;
5	y=0,5sin(2x-1)+3; y+2-ln(x-5)=0;	10	3y+3-cos2x=0; y=2x-3-1;

3. Пределы.

Одним из основополагающих понятий математического анализа является понятие предела переменной величины. Рассмотрим последовательность õ_n=1/n. Ясно, что чем больше номер n тем меньшее значение принимает величина õ_n, всегда оставаясь при этом положительной. В такой ситуации говорят, что с ростом номера n величина õ_n стремится (приближается) к нулю. Точное определение понятия предела числовой последовательности таково:

Число а называется пределом последовательности õ₁,õ₂, . . . õ_n, . . ., если для любого положительного числа  найдется такой номер N=N(), что для всех n>N выполняется неравенство x_n-a<. В этом случае пишут

.

Число А называется пределом функции при ха, если для любого положительного числа  найдется такое положительное =(), что f(x)-A< как только x-a<. Это записывают так: . Условно пишут так , если f(x)>M при x-a<, где М - произвольное сколь угодно большое положительное число. В этом случае функцию f(x) называют бесконечно большой ïðè õà.

Функция (х) называется бесконечно малой при ха, если (x)0 при xа. Если ха и при этом x<a, то употребляют запись ха-0: если же ха и x>a, то пишут так: ха+0. Числа f(a-0)= è f(a+0)= называют соответственно левым и правым пределом функции в точке а.

Для существования предела функции f(x) в точке а необходимо и достаточно, чтобы f(a-0)=f(a+0).

Практическое вычисление пределов основано на следующих теоремах:

Если существуют пределы è , òî

1. =

2. = .

3. 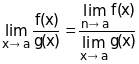åñëè 0.

Используются также следующие пределы:

1. - первый замечательный предел.

2.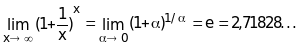 -второй

замечательный предел.

Логарифм числа х по основанию е называется натуральным логарифмом и обозначается lnx.

При вычислении пределов полезно также иметь в виду следующие равенства:

, , .

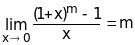Пример 1.

Решение. При х4 числитель дроби стремится к числу 54+2=22, а знаменатель - к числу 24+3=11. Следовательно,

.

Пример 2. .

Решение. Здесь числитель и знаменатель дроби неогра-ниченно возрастают при х (в такой ситуации говорят, что имеет место неопределенность вида /). Разделим числитель и знаменатель дроби на старшую степень переменной х, то есть на х³:

= .

Пример 3. .

Решение. При х1 числитель и знаменатель дроби стремятся к нулю (неопределенность вида 0/0). Выделим в числителе и знаменателе дроби множители, за счет которых они стремятся к нулю:

=

.

Пример 4. .

Решение. Здесь имеет место неопределенность вида (-). Умножим и разделим данное выражение на сумму составля-ющих его корней:

=

=

= =

= =

= =

Пример 5. .

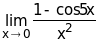Решение. Здесь мы имеем дело с неопределенностью вида (0/0). Воспользуемся первым замечательным пределом:

= =

= .

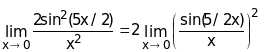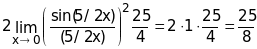Пример 6. .

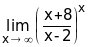Решение. В основании степени выделим целую часть:

Таким образом, при х данная функция представляет собой степень, основание которой стремится к единице, а показатель - к бесконечности (неопределенность вида 1^). Преобразовав эту функцию так, чтобы применить второй замечательный предел, получим:

= .

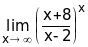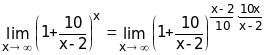Òàê êàê 10x/(x-2)10 ïðè õ, òî 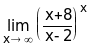=e¹⁰.

Задача 10. Вычислить пределы не применяя правило Лопиталя.

N	Условия
1
2
3
4
5
6
7
8
9
10