2. Прямоугольные и полярные координаты на плоскости.

Если на плоскости задана прямоугольная декартова система координат ХОY, то точку М этой плоскости, име-ющую координаты x и y, будем обозначать М(x,y).

Расстояние между точками A(x_A,y_A) и B(x_B,y_B) из теоремы Пифагора определяется по формуле:

B частности, расстояние от точки М(x,y) до начала системы координат может быть вычислено так:

.

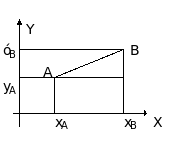
Если точка С(x_C,y_C) лежит на отрезке АВ и делит его в заданном отношении , то есть АС:CB=, то координаты этой точки определяются по формулам

,

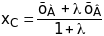В частности, при =1 получаем формулы для вычисления координат середины отрезка АВ

, .

Площадь треугольника с вершинами в точках A(x_A,y_A), B(x_B,y_B) è Ñ(x_Ñ,y_Ñ) может быть вычислена с помощью определителя третьего порядка:

S=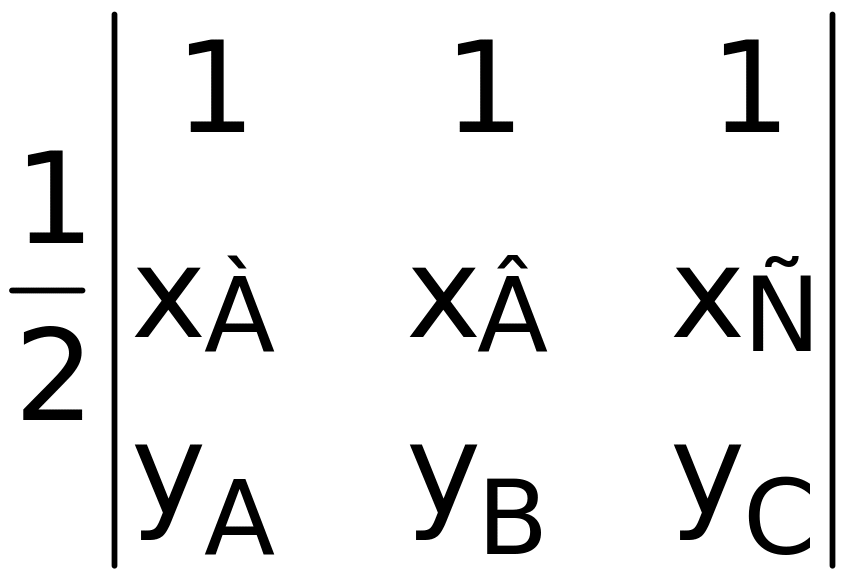

В полярной системе координат положение точки М на плоскости определяется ее расстоянием =ОМ от полюса О ( - полярный радиус-вектор точки) и углом ,

X

Y

M



x

y



образованным отрезком ОМ с полярной осью ОХ ( - полярный угол точки). Поляр-ный угол считается положитель-ным при отсчете его от поляр-ной оси против часовой стрел-ки.

Если полюс полярной систе-мы координат совместить с началом декартовой системы ко-ординат, а полярную ось направить по положительному направлению оси ОХ, то прямоугольные x и y и полярные  и  координаты точки М будут связаны соотношениями:

x = cos, y = sin

 = ,  = arctg(y/x)

Пример 1. Один конец отрезка длины с перемещается по оси абсцисс, а другой - по оси ординат. Найти уравнение линии, описываемой серединой этого отрезка.

Решение. Пусть М(x,y) - середина отрезка. Длина отрезка ОМ (как длина медианы в соответствующем прямоугольном

треугольнике) равна половине гипотенузы, то естьОМ = с/2. С другой стороны

X

Y

x

y

M

ÎÌ =

(расстояние от точки М до начала системы координат).

Таким образом, приходим к уравнению

=ñ/2, èëè x²+y²=(c/2)².

Это уравнение определяет окружность радиуса с/2 с центром в начале системы координат.

Пример 2. Составить уравнение линии, расстояние от каждой точки которой до точки F(1/4,0) равно расстоянию от этой же точки до прямой x=-1/4.

Решение. Рассмотрим произвольную точку М(x,y), лежащую на искомой линии. Расстояние от точки М до точки F можно найти из формулы расстояния между двумя точками:

ÌF = .

Пусть К - основание пер­пендику­ляра, опущенного из точки М на прямую x=-1/4, а N – основание перпендикуляра, опущенного из точки К на ось ОY. Тогда, как легко видеть,

KM=KN+NM=x+1/4.

Поскольку по условию задачи MN=MF, то координаты любой точки на нашей кривой связаны соотношением:

=x+1/4,

èëè

x²-1/2x+1/16+y²= x²+1/2x+1/16,

X

F

M

N

ò

Y

K

î åñòü x=y². Линия, определяемая этим урав-нением, представляет со-бой параболу.

Пример 3. Составить уравнение линии, произведение рас-стояний каждой точки которой до двух данных точек F₁(-a,0) è F₂(a,0) есть величина постоянная, равная а².

Решение. Зафиксируем произвольную точку М(x,y) на искомой кривой. Ее расстояния до точек F₁ è F₂ соответственно равны

d1= è d2= .

По условию задачи d1d2=a² и, следовательно, наша кривая имеет уравнение

 = à².

Возводя обе части последнего равенства в квадрат, получим

(x²+a²+y²+2ax)(x²+a²+y²-2ax)=a⁴

^èëè

(x²+a²+y²)²-4à²x²=a⁴

и окончательно

(x²+y²)² = 2a²(x²-y²)

Кривая с таким уравнением называется лемнискатой.

Найдем уравнение этой линии в полярной системе координат. В последнем уравнении перейдем к полярным координатам x=cos, y=sin :

(²cos²+²sin²)² = 2a²(²cos²-²sin²),

⁴(cos²+sin²)² = 2a²²(сos²-sin²).

Следовательно, уравнение лемнискаты ²=2a²cos2 .

Задача 4. Построить линии в полярной системе координат и найти их уравнения в декартовой системе координат.

1. r=3/(1-cosj) 2. r=2/(2-cosj) 3. r=4sinj+cosj

4. r=4/(1+sin2j) 5. r=4/(1-sinj) 6. r=3/(2+sinj)

7. r=3/(2-3cosj) 8. r=5/(3+3sinj) 9. r=3/sin(j-p/4)

10. r=10/(3-3cosj)