5. Преобразование координат и упрощение уравне- ний кривых второго порядка.

Пусть на плоскости заданы две системы координат хоу и ХОУ. соответствующие оси координат которых параллельны и начало системы хоу находится в точке О(a,b) относительно системы ХОУ. Тогда связь между координатами некоторой точки М в этих системах координат определяется так:

x =X+a y=Y+b.

Если начала систем координат ХОУ и хоу сов-падают и оси системы хоу повернуты относительно осей системы ХОУ на угол  (отсчитанный против часовой стрелки), то зависимость меж-ду координатами некоторой точки плоскости определяется так:

x= Xcos+Ysin

y=-Xsin+Ycos

Всякое уравнение второй степени относительно координат х и у

Àõ²+Bxy+Cy²+Dx+Ey+F=0

определяет либо пару прямых (в случае, когда его левая часть представима в виде произведения двух линейных множителей), либо одну из кривых второго порядка: эллипс, гиперболу, или параболу. Чтобы определить вид соответствующей кривой, ее общее уравнение с помощью подбора подходящей системы координат следует привести к каноническому виду. Сначала не­обходимо повернуть оси системы координат на такой угол , чтобы в новой системе координат ХОУ уравнение кривой не содержало про-изведения координат ХУ, то есть чтобы в новой системе координат уравнение кривой имело вид:

AX²+BY²+CX+DY+E=0

Затем с помощью процедуры выделения полных квадратов привести уравнение кривой к одному из видов:

A(X-a)²  B(Y-b)²=C,

ëèáî

(X-a)²=A(Y-b), A(X-a)=(Y-b)²

Наконец, с помощью параллельного переноса начала системы координат x'=X-a, y'=Y-b привести уравнение кривой к каноническому виду.

Пример 1. Привести к каноническому виду уравнение кривой x²-9y²+2x+36y-44=0.

Решение. Наше уравнение не содержит произведения координат, поэтому производить поворот осей координат нет необходимости. Выделим в уравнении полные квадраты:

(x²+2x+1-1)-9(y²-4y+4-4)=44

(x+1)²-9(y-2)²=44+1-36, (x+1)²-9(y-2)²=9.

Произведем параллельный перенос осей координат X=x+1, Y=y-2 (начало новой системы координат будет находиться в точке О(-1,2)). В новой системе координат уравнение кривой примет вид:

X²+9Y²=9, èëè X²/9-Y²=1.

Это уравнение определяет гиперболу с асимптотами Y=1/3X.

Задача 6. Привести кривую второго порядка к канони-ческому виду, определить ее параметры и построить ее график

N		N
1	-x2-y2+2x-4y-1=0	6	x2+y2-8x-8y+7=0
2	2x2+2y2-2x-2y-1=0	7	x2+y2-8x-4y-5=0
3	-2x2-2y2-6x+6y-1=0	8	x2+y2-2x+2y-7=0
4	-3x2-3y2-6x+4y-3=0	9	9x2-4y2+36x+16y=75
5	-2x2-2y2+10x-10y=7	10	4x2-8y2-y+7=0

6. Векторы.

Вектором называется направленный отрезок. Всякий вектор à характеризуется своей длиной à и направлением.

Сумма векторов a è b, начала которых совпадают, изображается вектором, с тем же началом и совпадающим с диагональю параллелограмма, построенного на этих векорах. Разность a-b изображается второй диагональю этого парал-лелограмма. Начало этого вектора находится в к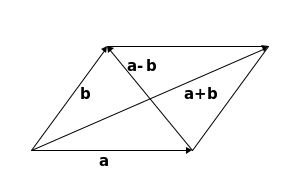 онце вектора b, а конец - в конце вектора a. Под произведением ma вектора a на число m понимается вектор, параллельный (коллинеарный) вектору a, длина которого равна ma, а направление совпадает с направлением вектора a для положительного m и противопо-ложно ему для отрицательного m. В частности, если m=1/a, то вектор a₀=ma=a/a имеет длину, равную единице, и направление, совпадающее с направлением вектора a. Этот вектор называют единичным вектором (ортом) вектора a.

Пусть в пространстве задана прямоугольная система координат ХОУ. На осях системы координат выберем векторы единичной длины i, j, k (орты), направления которых совпадают с положительным направлением соответствующей оси. Тогда каждый вектор a может быть представлен в виде суммы трех векторов

a=a_xi+a_yj+a_zk,

ãäå a_x, a_y è a_z - проекции вектора à на соответствующие оси системы координат. Такое представление вектора à называет-ся его разложением по координатным ортам. Длина вектора à может быть вычислена так

Направление вектора à определяется углами ,  и , образованными им с осями системы координат. Косинусы этих углов (направляющие косинусы вектора) вычисляются так:

cos=a_x/a, cos=a_y/a, cos=a_z/a.

Направляющие косинусы вектора связаны соотношением

cos²+cos²+cos²=1.

Арифметические операции над векторами, разложенными по координатным ортам, осуществляются покоординатно.

Вектор OM начало которого совпадает с началом системы координат, а конец - с точкой М(x.y.z), называют радиус-вектором точки М:

r=r(M)=xi+yj+zk .

Вектор AB, имеющий начало в точке А и конец в точке В, может быть записан в виде AB=r(B)-r(A), поэтому его разложение по ортам имеет вид:

AB=(x_B-x_A)i+(y_B-y_A)j+(z_B-z_A)k.

Его длина совпадает с расстоянием между точками А и В:

AB=

Скалярным произведением векторов a è b называется число, равное произведению длин этих векторов и косинуса угла  между ними:

ab = abcos.

Заметим, что число bcos есть величина проекции вектора b на направление вектора à: ïð_ab=bcos. Поэтому, на языке проекций скалярное произведение векторов может быть записано так:

ab = a ïð_ab= b ïð_ba

Свойства скалярного произведения.

1. aa=a².

2. ab=0, если один из сомножителей равен нулю, либо эти векторы перпендикулярны (cos = 0).

3. ab=ba (переместительный закон).

4. a(b+c)=ab+ac (распределительный закон)

5. (ma)b=a(mb)=m(ab) (сочетательный закон).

Если векторы a è b разложены по координатным ортам a=a_xi+a_yj+a_zk, â=â_xi+â_yj+â_zk, то их скалярное произведение может быть вычислено так:

ab=a_xb_x+a_yb_y+a_zb_z.

Векторным произведением ab векторов a è b называется вектор ñ, обладающий следующими свойствами:

1. Его длина равна площади параллелограмма, по-строенного на векторах à è b (c=absin, где  - угол между векторами à è b).

2. Он перпендикулярен плоскости векторов à è b.

3. Направление его таково, что векторы a, b è c ори-ентированы по отношению друг к другу соответственно как орты i, j è k (образуют правую тройку).

Свойства векторного произведения.

1. ab=-ba.

2. ab=0, если один из сомножителей равен ну-лю, либо векторы à è b параллельны (sin = 0).

3.(ma)b=a(mb)=m(ab). (сочетательный закон)

4. a(b+c)=ab+ac (распределительный закон).

Векторные произведения координатных ортов:

ii=jj=kk=0,

ij=-ji=k; jk=-kj=i; ki=-ik=j.

Векторное произведение двух векторов a=a_xi+a_yj+a_zk, â=â_xi+â_yj+â_zk может быть вычислено с помощью фор-мального определителя третьего порядка:

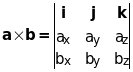
Раскрывать этот определитель всегда следует по первой строке.

Смешанным произведением векторов à, b è c называется скалярное произведение вектора ab на вектор ñ. Абсолютная величина смешанного произведения трех векторов à, b è c равна объему параллелепипеда, построенного на этих векторах.

Свойства смешанного произведения.

1. Смешанное произведение трех векторов равно нулю, если один из сомножителей равен нулю, либо два из них коллинеарны, либо все они параллельны одной и той же плоскости (компланарны).

2. Смешанное произведение не изменится, если в нем поменять местами знаки векторного и скалярного произведений, то есть (ab)c=a(bc), поэтому смешанное произведение записывается в виде abc.

3. Смешанное произведение не изменяется при круговой перестановке его сомножителей abc=bca=cab.

4. При перестановке любых двух своих сомножителей смешанное произведение изменяет только знак.

Если векторы разложены по координатным ортам

a=a_xi+a_yj+a_zk, â=â_xi+â_yj+â_zk, c=c_xi+c_yj+c_zk, то их смешан-ное произведение может быть вычислено с помощью опре-делителя третьего порядка

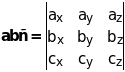
Как отмечалось, объем параллелепипеда, построенного на векторах a, b, c вычисляется так: V=abc. Объем треугольной пирамиды, построенной на этих векторах равен шестой части объема параллелепипеда: V=1/6abc.

Пример 1. Найти угол между векторами

à=i+2j+3k, â=6i+4j-2k.

Решение. Так как ab=abcos, òî . Вычислим скалярное произведение векторов à è â и их длины:

ab=16+24+3(-2) = 8,

a= , b= .

Следовательно,

, è

Пример 2. Вычислить площадь треугольника с вершинами в точках A(1,1,1), B(2,3,4) и C(4.3.2).

Решение. Найдем векторы ÀÂ è ÀÑ:

ÀÂ=(2-1)i+(3-1)j+(4-1)k=i+2j+3k

ÀC=(4-1)i+(3-1)j+(2-1)k=3i+2j+k.

Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах ÀÂ è ÀÑ, поэтому найдем векторное произведение этих векторов:

ABAC=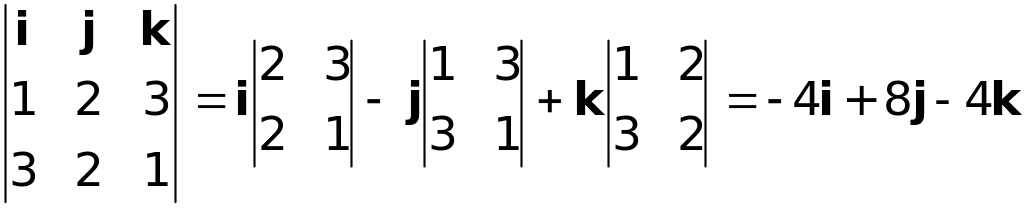

Следовательно,

S_ABC =

Пример 3. Найти объем треугольной пирамиды с вершинами в точках А(2,2,2), B(4,3,3), C(4,5,4), D(5,5,6).

Решение. Найдем векторы à=ÀÂ, â=ÀÑ, ñ=ÀD, образующие ребра пирамиды,

à=r(B)-r(A)=2i+j+k,

b=r(C)-r(A)=2i+3j+2k,

c=r(D)-r(A)=3i+3j+4k

и вычислим смешанное произведение этих векторов

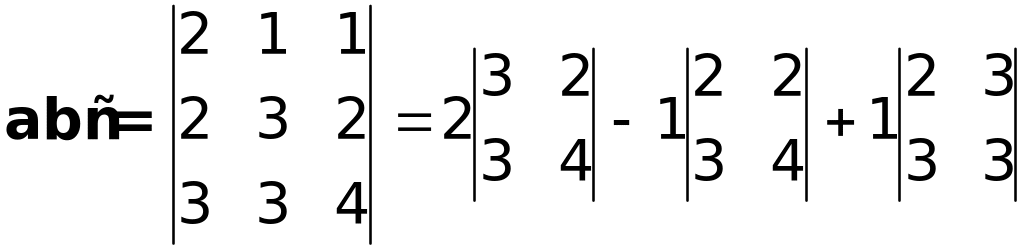=26-12-13=7.

Так как объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах à, â è ñ, òî V=7/6.

Задача 7. Даны точки A, B, C, D. Найти:

1. [À´ÀÑ]×(2CD- AD)

2. AB×[3AB´CD].

3. Проекцию вектора CD на направление

вектора ÀÑ.

4. Разложение вектора CD по векторам

AD,BC,AC.

5. Площадь треугольника АВС.

6. Óãîë ACD.

7. Высоту пирамиды ABCD, опущенную

из вершины В.

N	A	B	C	D	N	A	B	C	D
1	(5,1,2)	(2,-3,0)	(4,7,-1)	(2,7,1)	6	(2,3,1)	(4,1,-2)	(6,3,7)	(7,5,-3)
2	(3,4,1)	(2,-4,0)	(1,-1,5)	(-2,3,1)	7	(1,1,-1)	(2,3,1)	(3,2,1)	(5,9,-8)
3	(5,6,7)	(2,-3,1)	(7,-8,8)	(3,-1,2)	8	(4,-1,3)	(-2,1,0)	(0,-5,1)	(3,2,-6)
4	(2,5,7)	(7,5,-2)	(5,7,2)	(-7,5,2)	9	(1,-1,2)	(2,1,2)	(1,1,4)	(6,-3,8)
5	(1,5,0)	(9,1,5)	(5,1,9)	(-1,-5,9)	10	(1,3,0)	(4,-1,2)	(3,0,1)	(-4,3,5)