3. Прямая линия.

Всякое уравнение первой степени относительно координат x и y, то есть уравнение вида

Ax+By+C=0,

где A,B,C - постоянные коэффициенты (причем A²+B²0) определяет на плоскости некоторую прямую. Это уравнение называют общим уравнением прямой.

Частные случаи расположения прямой.

1. С=0, А,В0. Прямая, определяемая уравнением, Ax+By=0, проходит через начало системы координат.

2. А=0, В0, С0. Прямая, определяемая уравнением, By+С=0 (или y=-C/B), параллельна оси ОХ.

3. В=0, А, С0. Прямая, определяемая уравнением, Ах+С=0 (или х=-C/А), параллельна оси ОY.

График прямой линии удобно строить по известным координатам любых двух ее точек , как правило, - точек ее пересечения с осями системы координат.

Если в общем уравнении прямой B0, то разрешив это уравнение относительно y, представим это уравнение в виде

y=kx+b,

где k=-A/B и b=-C/B. Это уравнение называют уравнением прямой с угловым коэффициентом, поскольку в нем

X

Y



x

b

y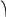

k=tg

- тангенс угла, образованного прямой с положительным на­правлением оси ОХ, а b=-C/B - ордината точки пересечения прямой с осью OY.

Если в общем уравнении прямой C0, то, разделив обе его части на -C, получим уравнение вида

,

где a=-C/A и b=-C/B. Его называют уравне­нием прямой в отрезках, поскольку в нем а - абсцисса точки пересе­чения прямой с осью ОХ, а b - ордината точки пересечения прямой с осью OY. Числа а и b называют отрезками прямой на осях координат.

Если обе части общего уравнения прямой умножить на число

,

которое называют нормирующим множителем, причем знак перед корнем выбрать так, чтобы выполнялось неравенство С > 0, то получим уравнение

xcos+ysin-p=0.

Это уравнение называют нормальным уравнением прямой. Здесь р - длина перпендикуляра, опущенного на прямую из начала системы координат, а  - угол, образованный этим перпендикуляром с положительным направлением оси ОХ ( , , ).

X

Y

₂



₁

Острый угол между двумя прямыми y=k₁x+b₁ è y=k₂x+b₂ может быть вычислен так:

(k₁=tg₁, k₂=tg₂)

Òàê êàê k₁ è k₂ - угловые коэффициенты прямых, то условие параллельности прямых имеет вид

k₁=k_2,

à условие их перпендикулярности -

k₁k₂=-1.

Уравнение прямой, имеющей заданный угловой коэффициент k и проходящей через заданную точку M(х₀,y₀), имеет вид

y-y₀=k(x-x₀).

Уравнение прямой, проходящей через две заданные точки M₁(õ₁,y₁) è M₂(õ₂,y₂) записывается в виде

,

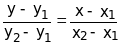а угловой коэффициент этой прямой может быть найден так

.

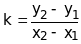Расстояние от точки М(х₀,y₀₎ до прямой Ax+By+C=0 может быть найдено из формулы:

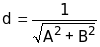Ax₀+By₀+C

Пример 1. Найти координаты точки пересечения прямых 3x-2y+1=0 и 2x+5y-12=0.

Решение. Так как искомая точка лежит на каждой из прямых, то ее координаты х и y удовлетворяют уравнению как первой, так и второй прямой, то есть являются решением системы уравнений

.

Решив эту систему, находим х=1, у=2, то есть прямые пересекаются в точке М(1,2).

Пример 2. Составить уравнение прямой, проходящей через точку М(-2,-5) и параллельной прямой 3х+4у+2=0.

Решение. Разрешив уравнение прямой относительно переменной у, получим у=(-3/4)x-1/2. Значит, угловой коэффициент нашей прямой равен -3/4. Из условия параллельности прямых угловой коэффициент k искомой прямой так же равен -3/4. Так как искомая прямая проходит через точку М, то она имеет уравнение у-у_M=k(x-x_M). Подставив в последнее уравнение координаты точки М и найденный угловой коэффициент, получим уравнение 3х+4у+2=0.

Пример 3. Даны уравнения высот х+у-2=0, 9х-3у-4=0 треугольника АВС и координата его вершины А(2,2). Составить уравнения сторон треугольника.

Решение. Легко проверить, что вершина А не лежит ни на одной из заданных высот (ее координаты не удовлетворяют уравнениям этих прямых). Пусть 9х-3у-4=0 - уравнение высоты ВВ₁ и х+у-2=0 - уравнение высоты СС_1.. Составим уравнение стороны АС, рассматривая ее как прямую, проходящую через точку А и перпендикулярную высоте ВВ₁. Угловой коэффициент высоты ВВ₁ k=9/3=3 из из условия перпендику­лярности прямых АС и ВВ₁ k_AC=-1/k=-3. Уравнение прямой АС запишем теперь как уравнение прямой, проходящей через точку А и имеющей заданный угловой коэффициент

ó-2=(-3)(õ-2), èëè õ+3ó-8=0

Аналогично последовательно найдем угловой коэффициент высоты СС₁ (k=-1), из условия перпендикулярности прямых - угловой коэффициент прямой AВ k_AB=1 и, наконец, уравнение прямой АВ

ó-2=õ-2 , èëè ó=õ.

Далее, точка В есть точка пересечения прямых АВ и ВВ₁, поэтому ее координаты являются решением системы уравнений, составленной из уравнений этих прямых В(2/3,2/3). Таким же образом найдем координаты вершины С: C(-1,3). Уравнение последней стороны треугольника АС теперь найдем как уравнение прямой, проходящей через две точки (А и С) с известными координатами:

, òî åñòü 7õ+5ó-8=0.

Задача 5. Даны три вершины треугольника A, B и C. Найти:

1. Уравнение и длину высоты AD.

2. Уравнение медианы AE.

3. Уравнение прямой, проходящей через

вершину A параллельно стороне BC.

4. Центр тяжести (точку пересечения медиан)

треугольника ABC.

5. Точку S, симметричную точке A относительно

прямой BC.

N	A	B	C	N	A	B	C
1	(3,4)	(-2,0)	(1,-2)	6	(1,5)	(-2,4)	(-4,-2)
2	(5,-1)	(-4,2)	(4,10)	7	(-3,6)	(2,-7)	(0,5)
3	(7,-1)	(0,3)	(2,-1)	8	(4,6)	(-3,5)	(0,1)
4	(1,7)	(-3,0)	(4,1)	9	(3,4)	(-3,1)	(2,4)
5	(1,5)	(-5,-2	(-3,5)	10	(1,1)	(4,5)	(-2,2)