6. Теоремы о дифференцируемых функциях.

Теорема Ролля. Пусть функция y=f(x) определена на интервале [a,b] и обладает следующими свойствами:

1. Она непрерывна на интервале [a,b].

2. Она дифференцируема на интервале (a,b).

3. На концах интервала она принимает равные

значения f(a)=f(b).

Тогда найдется точка c(a,b) такая, что f'(c)=0.

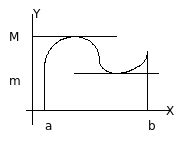
Геометрически теорема Pолля гарантирует существование такой точки с внутри интервала [a,b], в которой угловой коэффициент касательной к графику функции равен нулю k=f'(c)=0, то есть эта касательная параллельна оси ОХ.

Теорема Лагранжа. Пусть функция y=f(x) определена на интервале [a,b] и обладает следующими свойствами:

1. Она непрерывна на интервале [a,b].

2. Она дифференцируема на интервале (a,b).

Тогда найдется точка c(a,b) такая, что f'(c)=

Геометрически тео-рема Лагранжа озна-чает, что на дуге АВ непрерывно диффе-ренцируемой кривой найдется внутренняя точка, в которой ка-сательная к кривой параллельна секущей АВ. (Заметим, что правая часть формулы Лагранжа представляет собой угловой коэф-фициент секущей АВ, а левая - угловой коэффициент касательной к графику функции с абсциссой в точке х=с).

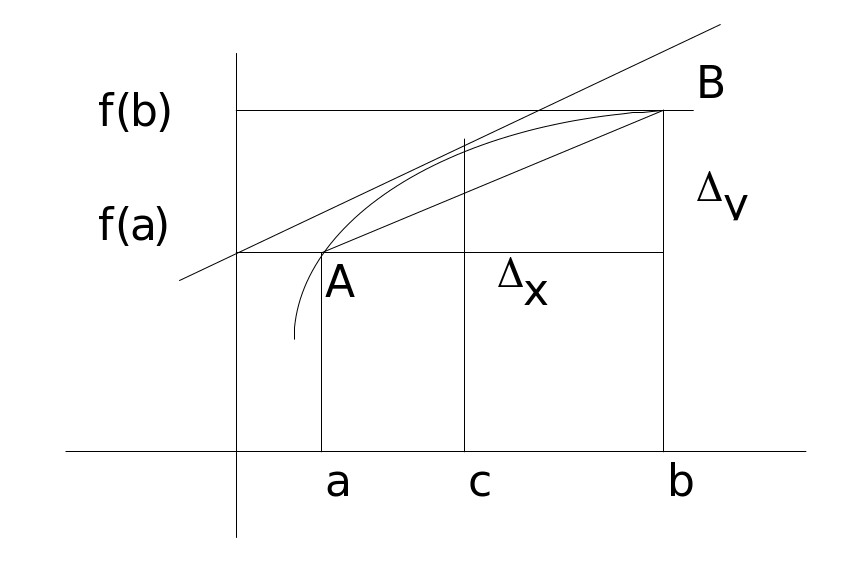
Формулу, фигурирующую в теореме Лагранжа, называют формулой Лагранжа или формулой конечных приращений. Если обозначить а=х, b=x+x, то формула Лагранжа примет вид:

f(x+x)=f(x)+f'(c)x

Естественным обобщением теоремы Лагранжа является

Теорема Коши. Если функции f(x) и g(x) непрерывны на интервале [a,b] и дифференцируемы на интервале (a,b), причем g(x)0, то найдется точка c(a,b) такая, что

Теорема Тейлора. Функция f(x), дифференцируемая n+1 раз на некотором интервале, содержащем точку а, может быть представлена в виде суммы многочлена степени n и остатка

,

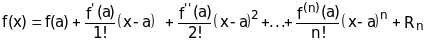
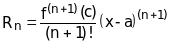для некоторого с=а+(х-а), причем 0<<1.

Напомним, что под знаком n! (n факториал) числа n пони-мается произведение всех натуральных чисел от 1 до n.

Теорема Лопиталя. Пусть в некоторой окрестности точки а (кроме, быть может, самой точки а) функции f(x) и g(x) дифференцируемы и f(a)=g(a)=0. Тогда

,

если последний предел существует.

Теорема Лопиталя является удобным инструментом для вычисления пределов, сводящихся к неопределенности вида 0/0. Правило Лопиталя также можно применять в случае неопределенности вида /. В случае неопределенностей вида 0 или - их следует преобразовать к неопределенности вида 0/0 либо /. Для раскрытия неопределенностей вида 0⁰ ⁰ èëè 1^ необходимо проло-гарифмировать данную функцию и предварительно вычис-лить предел ее логарифма.

Пример 1. На дуге АВ кривой у=2х-х² найти точку, в которой касательная параллельна секущей АВ, если А(1,1) и В(3,-3).

Решение. Функция y=2х-х² дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 найдется точка с, удовлетворяющая равенству у(b)-y(a)=y'(c)(b-a), где y'=2-2x. Подставив соответствующие численные значения, получим (23-3²)-(21-1²)=(2-2c)(3-1). Откуда с=2 и у(2)=0. Значит, условию задачи удовлетворяет точка М(2,0).

Пример 2. .

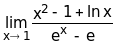Решение. При х1 числитель и знаменатель дроби стремятся к нулю, то есть мы имеем дело с неопределенностью вида 0/0 и поэтому применимо правило Лопиталя:

.

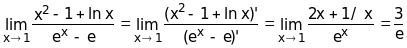Пример 3. .

Решение. Здесь неопределенность вида 0, поэтому представим произведение функций в виде частного и, получив неопределенность вида /, применим правило Лопиталя.

Пример 4. .

Решение. Здесь неопределенность вида 0⁰. Обозначим А= . Тогда из непрерывности логарифма

lnA=ln( )=

=

=

Следовательно, А=е⁰=1.