4. Кривые второго порядка.

Окружностью называется множество точек на плоскости, равноудаленных от данной точки, называемой центром. Если центр расположен в точке А(a,b), а радиус окружности равен R, то из формулы расстояния между двумя точками на плоскости уравнение такой окружности имеет вид:

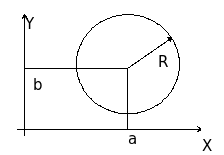
(x-a)²+(y-b)²=R²

В частности, если центр окружности совпадает с на-чалом системы координат (a=b=0), то уравнение такой окружности имеет вид:

x²+y²=R²

Эллипсом называется множество точек на плоскости, сумма расстояний которых до двух заданных точек, называемых фокусами, есть величина постоянная. Если эту постоянную обозначить через 2а, а фокусы эллипса поместить на оси ОХ, симметрично относительно начала системы координат, F₁(-c,0), F­­₂(c,0), то уравнение эллипса будет иметь вид:

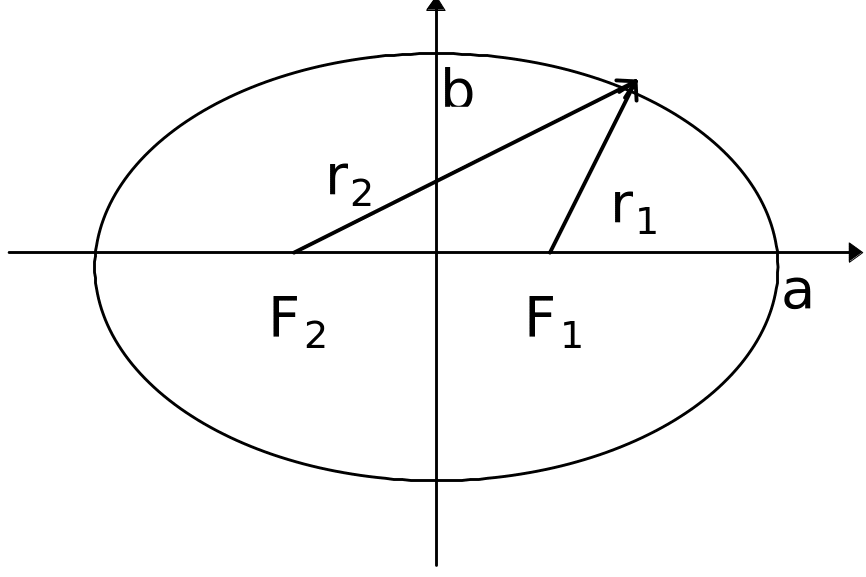
ãäå b²=à²-ñ². Числа a и b называют соответственно большой и малой полуосями эллипса, поскольку точки с координатами (a,b) явля­ются "вершинами" эллипса. Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом e=c/a. Так как для эллипса 2c<2a, то эксцентриситет эллипса строго меньше единицы. Расстояния от некоторой точки эллипса до его фокусов называют фокальными радиусами-векторами и обозначают r₁ è r_2­. По определению эллипса для любой его точки

r₁+r₂=2à.

Фокальные радиусы-векторы выражаются через абсциссу его точки по формулам: r₁=a-ex (правый радиус-вектор) и r₂=а+ex (левый радиус-вектор).

à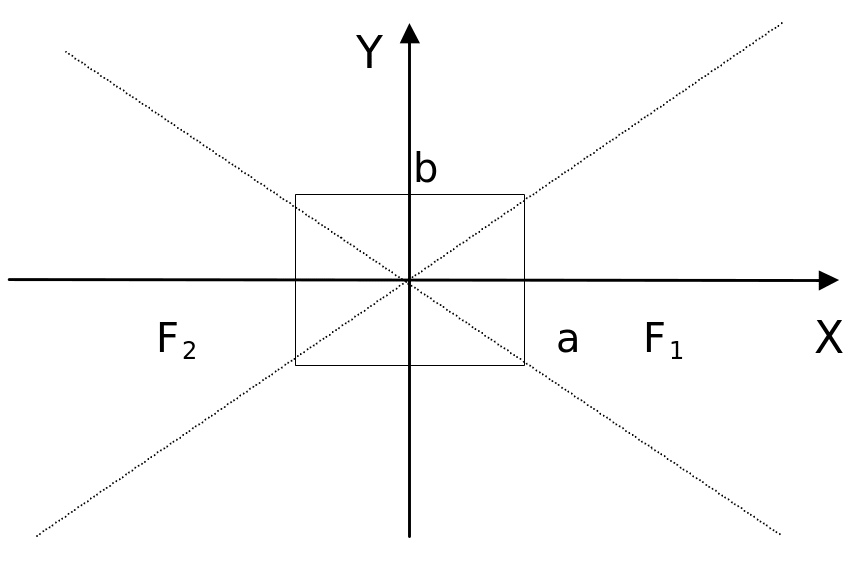 иперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная. Если эту постоянную обозначить через 2а и фокусы гиперболы поместить в точках F₁(-c,0), F₂(c,0), то уравнение такой гиперболы будет иметь вид:

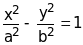ãäå b²=c²-a².

Гипербола состоит из двух ветвей и симметрична относительно осей координат. Точки A₁(-à,0) è À₂(а,0) называются вершинами гиперболы, а числа а и b - соответственно ее действительной и мнимой осями. Прямая линия называется асимптотой гиперболы, если расстояние от точки М(х,у), лежащей на гиперболе, стремится к нулю при х+ и х-. Гипербола имеет две асимптоты, уравнения которых у=(b/a)х. Для построения асимптот гиперболы необходимо построить прямоугольник со сторонами х=а, у=b, тогда диагонали этого прямоугольника и будут асимптотами гиперболы.

Отношение е=с/a называется эксцентриситетом гиперболы. Для любой точки М(х,у) гиперболы ее правый r₁ и левый r₂ фокальные радиусы-векторы могут быть вычислены так r₁=ex-a , r₂=ex+a, если точка лежит на правой ветви гиперболы и r₁=-ex+a, r₂=-ex-a, если точка лежит на левой ветви гиперболы.

Параболой называется множество точек на плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если расстояние от фокуса до директрисы параболы обозначить через р, ее фокус поместить в точку F(p/2,0), а директрису совместить с прямой х=-р/2, то уравнение параболы будет иметь вид:

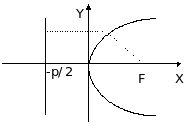
y² = 2px

Эта парабола симметрична относительно оси ОХ. Уравнение х²=2ру определяет параболу, симметричную относи-тельно оси ОУ. При р>0 ветви этих парабол направлены по положительному направлению соответствующей оси, а при р<0 - по отрицательному. Длина фокального радиуса-вектора параболы y²=2px может быть вычислена так: r=x+p/2.

Пример 1. Найти координаты центра и радиус окружности .

Решение. Разделим обе части уравнения на 2 и сгруп-пируем его члены

õ²-4õ+ó²+5/2y=2.

Дополним выражения х²-4õ è ó²+5/2y до полных квадратов, прибавив к первому из них 4, ко второму - (5/2)², одновременно добавив такие же слагаемые в правую часть уравнения

(x²-4x+4)+( y²+5/2y+25/4)=2+4+25/4

èëè

(x-2)²+(y+5/2)²=121/16

Таким образом, координаты центра окружности а=2, b=5/2 и радиус окружности R=11/4.

Пример 2. Составить уравнение множества точек плоскости, расстояния которых от точки А(0,1) в два раза меньше расстояния до прямой у-4=0.

Решение. Пусть М(х,у) - произвольная точка этого множества. Тогда из формулы расстояния между двумя точками AМ= . Если d - расстояние от точки М до прямой у=4, то, как легко видеть, d=у - 4. По условию задачи АМ=d/2, следовательно, координаты точки М связаны соотношением х²+(ó-1)²=(ó-4)²/4. После тождественных преобразований получим уравнение х²/3+y²/4=1, которое определяет эллипс с полуосями а= , b=2.

Пример 3. На правой ветви гиперболы х²/16-y²/9=1 найти точку, расстояние которой до правого фокуса вдвое меньше ее расстояния до левого фокуса.

Решение. Для нашей гиперболы а=4, b=3 и, значит, , е=c/a=5/4. Для правой ветви гиперболы фокальные радиусы-векторы определяются по формулам r₁=ex-a , r₂=ex+a и, значит, в нашем случае r₁=5/4x-4, r₂=5/4х+4. По условию задачи r₁=r₂/2, значит, для абсциссы точки М имеем уравнение 5/4x-4=(5/4x+4)/2, откуда х=48/5. Абсциссу точки М найдем из уравнения гиперболы:

.

Таким образом, условию задачи удовлетворяют две точки M₁(48/5,3/5 ) è M₂(48/5,-3/5 ).

Пример 4. Составить уравнение параболы с вершиной в начале системы координат, симметричной относительно оси ОУ и отсекающей на биссектрисе первого и третьего координатных углов хорду длиной .

Решение. Из условия задачи наша парабола имеет уравнение х²=2ру. Так как указанная биссектриса имеет уравнение у=х, то она пересекает параболу в точках О(0,0) и М(2р,2р) (точки пересечения двух линий - это решения системы уравнений, определяющих эти линии). Длина хорды ОМ определяется как расстояние между двумя точками: , откуда 2р=8. Следовательно, искомое уравнение имеет вид х²=8ó.