8.4. Сложение гармонических колебаний

8.4.1. Векторное и символическое представление

гармонических колебаний

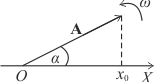
Гармонические колебания часто представляют в виде равномерно вращающегося вектора А, длина которого равна амплитуде колебаний А, а угловая скорость ω – круговой частоте коле-

Рис. 8.9

баний ω. Действительно, если построить вектор А длины А, образующий с осью X угол и привести его во вращение против часовой стрелки с угловой скоростью ω, то угол поворота этого вектора будет изменяться со временем по закону , а величина его проекция на ось X – по гармоническому закону x = Acos(ωt + ), что и смещение x при гармонических колебаниях (рис. 5.9).

Широко используется и так называемый символический способ изображения гармонических колебаний. Он основан на формуле Эйлера для комплексных чисел iAsinφ = = где А – модуль комплексного числа z т.е. – его аргумент, – реальная часть комплексного числа z (x = ), 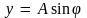– его мнимая часть (y = звездочка обозначает комплексное сопряжение. Следовательно, функция (5.3), описывающая гармонические колебания, есть реальная часть комплексного числа z, модуль которого равен амплитуде колебаний А, а его аргумент –фазе колебаний. При этом символ Re опускают и пишут

(5.5)

или где – комплексная амплитуда колебания.

Легко убедиться, что функция (5.5) периодическая с периодом и удовлетворяет дифференциальному уравнению (5.1).

8.4.2. Сложение колебаний одного направления одинаковых частот.

Для гармонических колебаний, как и для любых механических движений справедлив принцип суперпозиции. Это означает, что если частица может совершать два каких-либо гармонических колебательных движения, то она может совершать и такое движение, которое является суммой этих двух движений – колебания можно складывать. Рассмотрим сначала сложение двух гармонических колебаний

одинакового направления (вдоль оси X) и одинаковой частоты ω. В этом случае результирующее движение частицы оказывается тоже гармоническим колебанием того же направления и той же частоты: Это непосредственно вытекает из свойства линейности дифференциального уравнения гармонического осциллятора (5.1). Действительно, если x₁ и x₂ являются решениями этого уравнения при данном значении ω, то и их сумма также является решением этого уравнения. А это и означает, что если x₁ и x₂ являются гармоническими колебаниями частоты ω, то и их сумма также будет гармоническим колебанием той же частоты и того же направления.

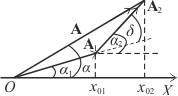
Для определения амплитуды А и фазы результирующего колебания воспользуемся методом векторных диаграмм. Этот ме-

Рис. 8.10

тод основан на векторном представлении гармонических колебаний и заключается в построении векторов, представляющих слагаемые и сумму колебаний, как показано на рис. 8.10. Фигура, изображенная на этом рисунке, и называется векторной диаграммой для данной задачи. Поскольку частоты колебаний одинаковы, вся изображенная на рис. 5.10 система векторов вращается как одно целое с угловой скоростью ω, причем проекция вектора А на ось X, определяющая смещение x в момент времени t равна сумме проекций x₁ и x₂ векторов А₁ и А₂. Из векторного треугольника на рис. 5.10 по теореме косинусов находим

(5.6)

где – разность фаз складываемых колебаний. Из того же треугольника найдем формулу и для фазы результирующего колебания:

Формула (5.6) показывает, что амплитуда результирующего колебания определяется не только амплитудами складываемых колебаний, но и разностью их фаз Поскольку 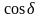может принимать как положительные, так и отрицательные значения, то при одних разностях фаз δ складываемые колебания будут усиливать друг друга, а при других ослаблять. Если складываемые колебания находятся в одинаковой фазе (синфазные), т.е. если разность фаз δ = 0 или кратно 2π, то амплитуда результирующего колебания будет иметь максимальное значение, равное – колебания усиливают друг друга. Если же складываемые колебания находятся в противофазе, т.е. если δ = π или любому нечетному числу π, то результирующее колебание будет иметь минимальное значение амплитуды, равное – колебания ослабляют друг друга, а при А₁ = А₂ полностью гасят друг друга.

Метод векторных диаграмм удобно применять и при сложении трех и более колебаний.