26.Перевірка статистичних гіпотез відносно коефіцієнтів регресії та кореляції

Однією із задач регресійного аналізу є порівняння коефіцієнтів регресії α, β з деякими очікуваними значен *. Такий аналіз можна здійснити шляхом перевірки статистич гіпотез:

Для їх перевірки використ крит: ,

які мають розподіл Ст’юдента з ступенями вільності k = n – 2. При рівні значущості і k = n – 2 на основі даного критерію гіпотези відхиляються, якщо та .

В економетричних досліджен досить поширеними щодо параметрів є гіпотези:

Прийняття гіпотези фактично означає відсутність лінійного зв’язку між x та y. Перевірку гіпотез також здійснюють для оцінки значущості коефіцієнта кореляції: .

Критерієм є випадкова величина: , яке має розподіл Ст’юдента з ступенями вільності k = n – 2. Якщо , то відхиляється, приймається , що свідчить про статистич значущість коеф кореляції.

33.Перевірка значущості коефіцієнтів регресії у випадку лінійної множинної регресії.

Як і у випадку парної регресії статистич значущість параметрів множинної регресії перевіряється на основі гіпотез: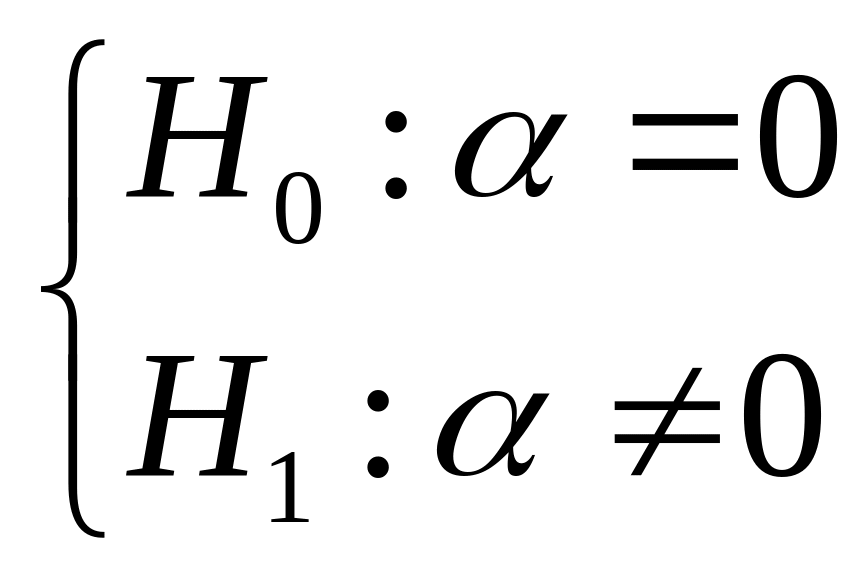 , 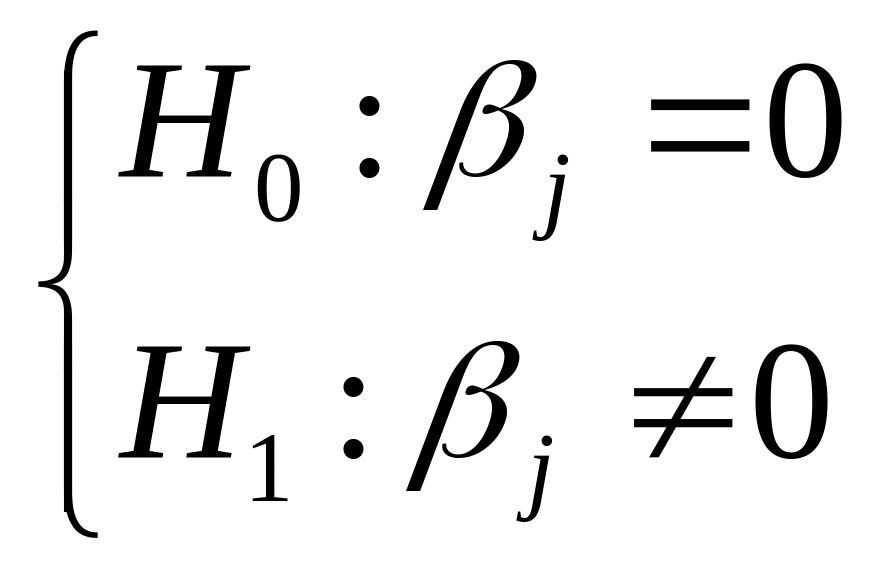- для цього використовують ta ,tb:

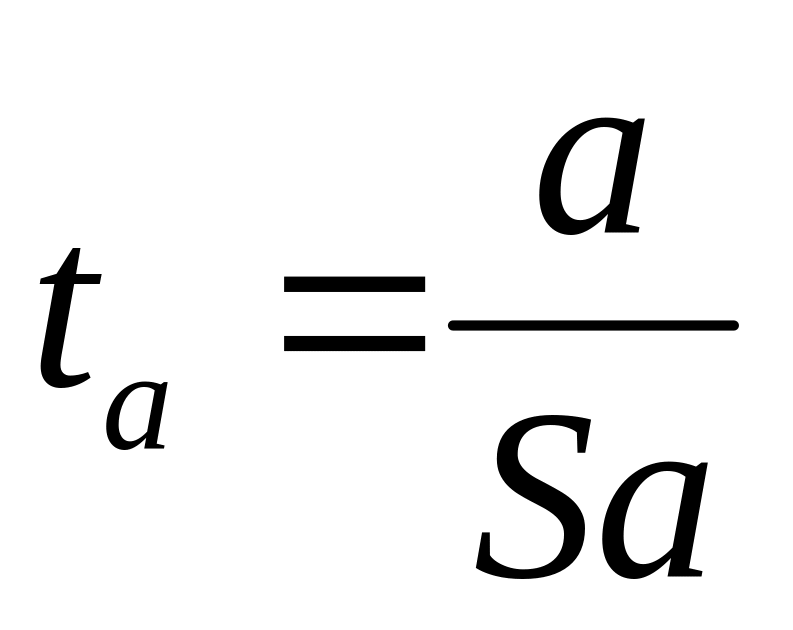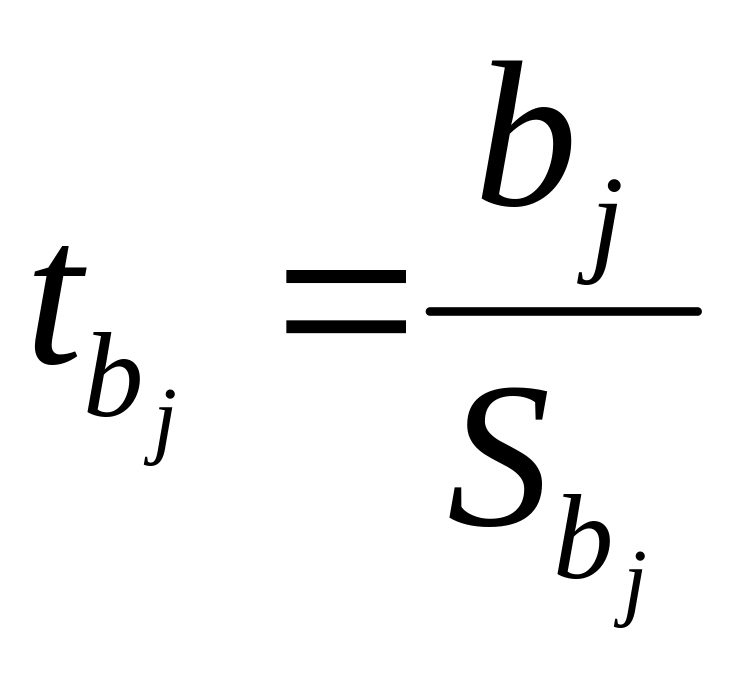, які мають розподіл Ст′юдента з числом ступенів вільності l=n-k=n-m-1.

Якщо 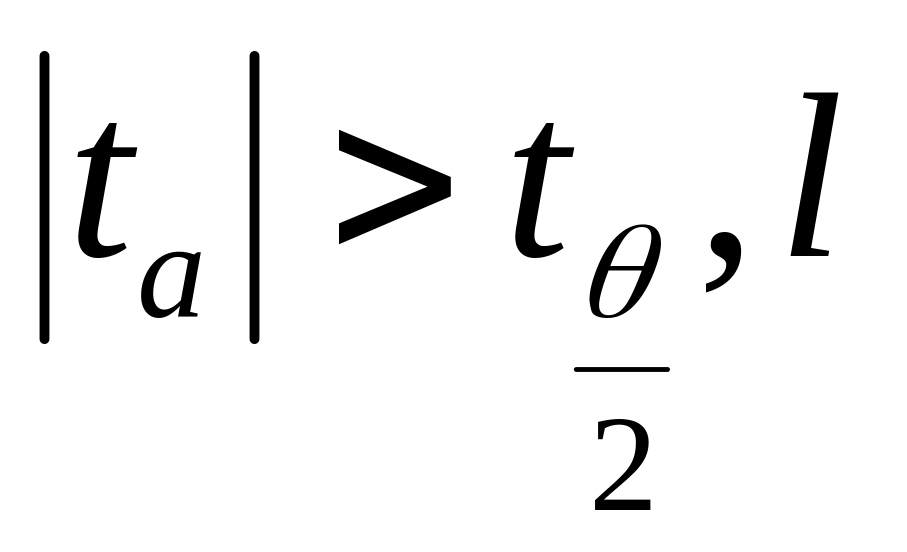- то а є статистично значущим, Якщо 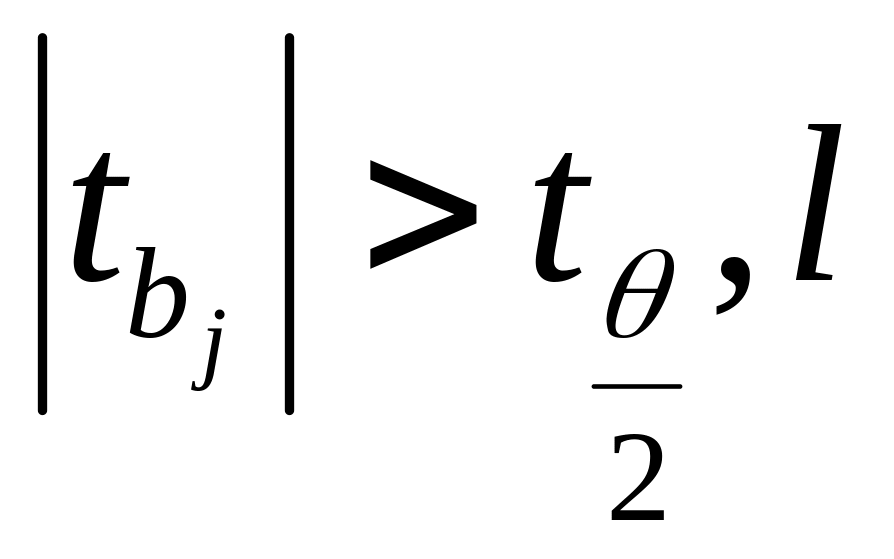- то в є статистично значущим

Значущість коеф детермінації ( ) перевіряється гіпотезами: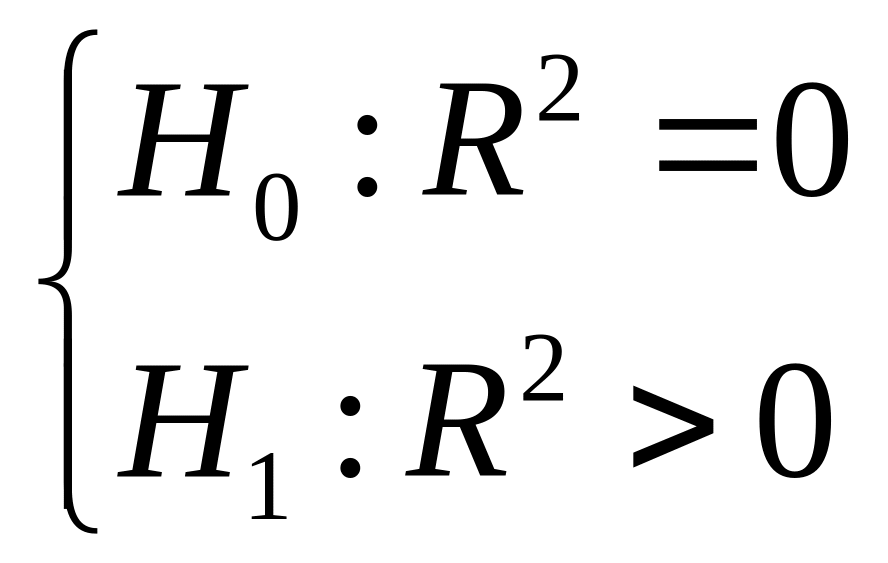 за допомогою f-статистики, що дорівнює: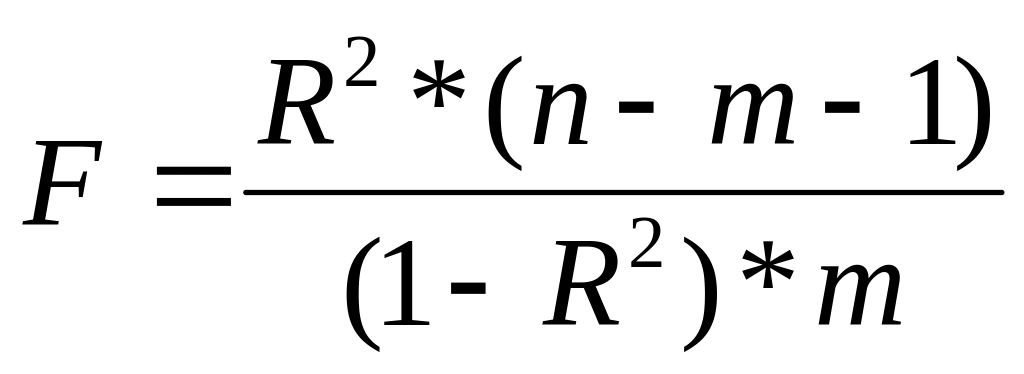 , яка має розподіл Фішера з ступенями вільності.

Якщо спостережуване значення то приймається альтернативна гіпотеза (H1), тобто вважається значущим.

Значущість коефіцієнта множинної кореляції можна перевірити за допомогою t-статистики:

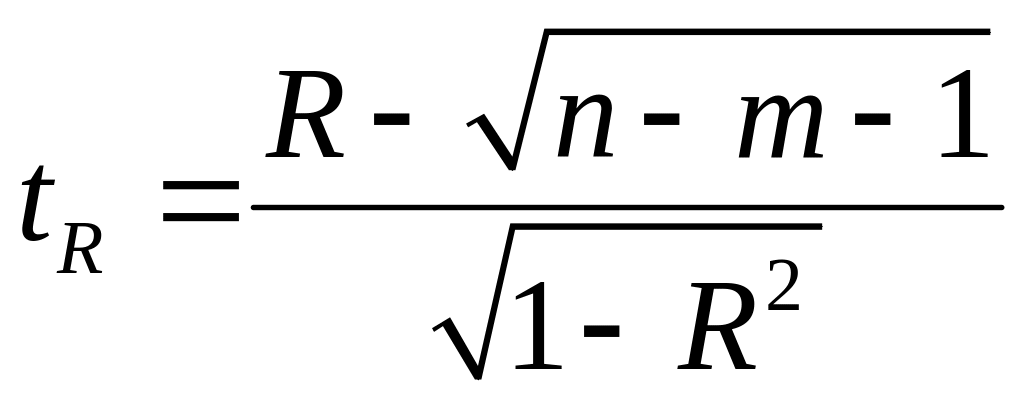яке має розподіл Ст′юдента з l=n-k=n-m-1 ступенями вільності.

Крім, і перевіряють значущість парної та частинної кореляції, тобто та цю перевірку також здійснюють за допомогою t-статистики:

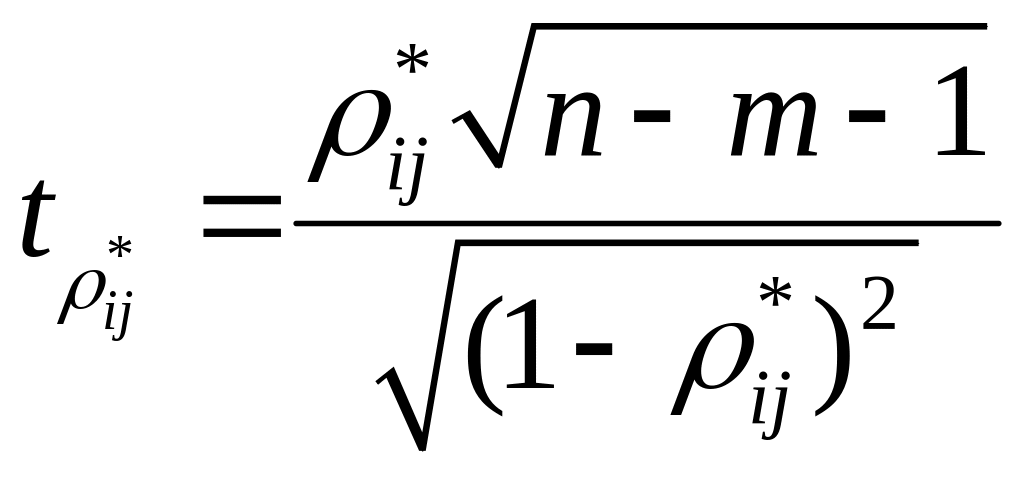
34.Перевірка значущості рівняння лінійної множинної регресії в цілому.

Часто вивч питання про значущість всіх коефіцієнтів регресії одночасно тобто перевіряється такі гіпотези: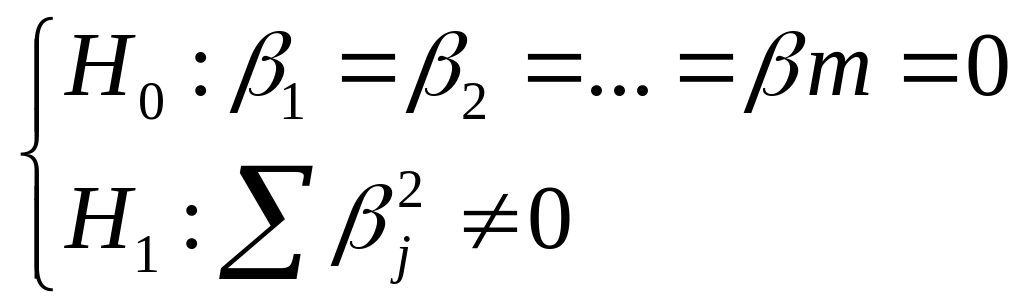 зміст гіпотез зрозуміліший тобто якщо виконується гіпотеза - то це означає, що побудоване рівняння регресії є не значущим і всі пояснюючі фактори не суттєво впливають на залежну змінну.

Перевірка цих гіпотез здійснюється за допомогою F- статистики: яка має розподіл Фішера з ступенями вільності.

Якщо спостережуване значення то приймається альтернативна гіпотеза( ), тобто модель вважається значущою.

Оск за допомогою цієї статистики перевіряється також значущість коефіцієнта детермінації, то перевірка цих гіпотез за своїм змістом є еквівалентною задачею. Саме тому значущість моделі еквівалентна значущості коефіцієнтів детермінації.

35.Інтервал оцінки парамет, функції ліній множин регресії та індивідуального значення залежної змінної.

Як і випадку парної регресії для побудови інтервальних оцінок за допомогою t-статистики: 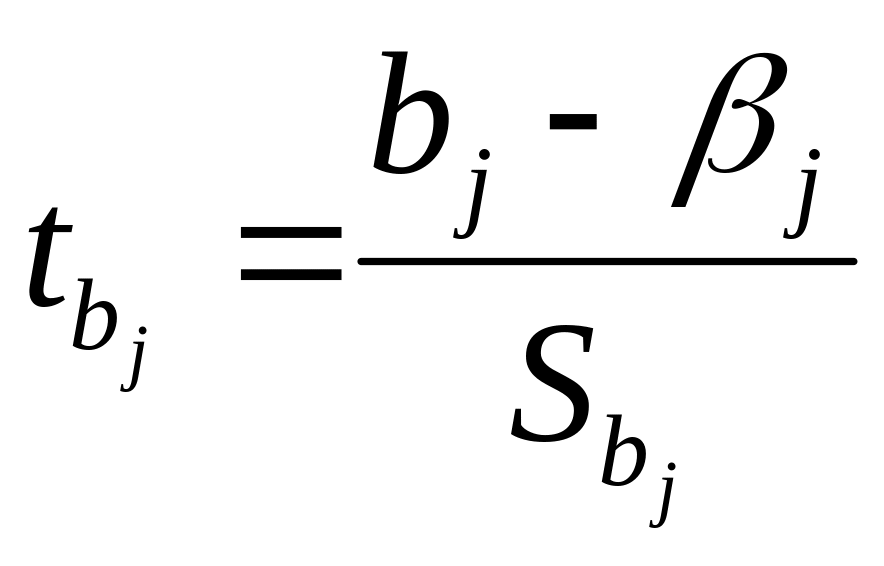, які мають розподіл Ст′юдента з l=n-m-1 ступенями вільності. При рівні значущості , тобто рівні надійності (1- ) інтервальні оцінки отримують з нерівності: використовуючи цю нерівність інтервальні оцінки для параметрів регресії визначаються так: 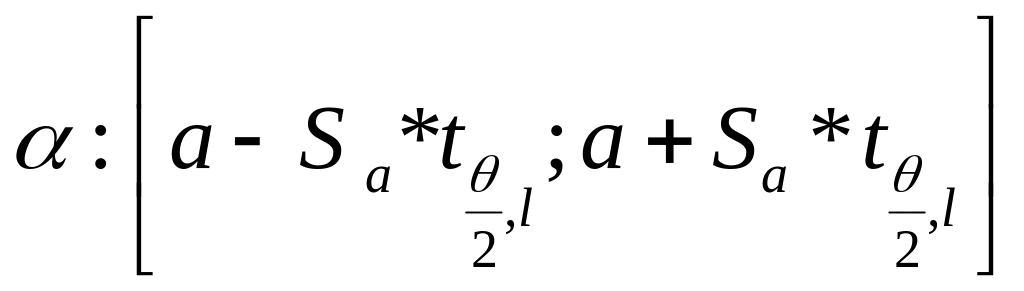, 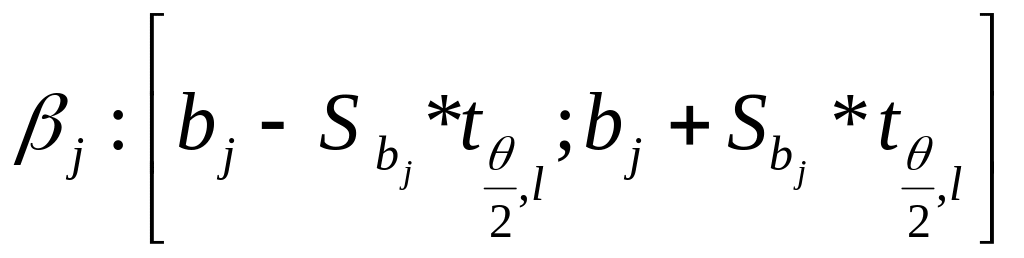- де знаходяться з дисперсійно-коваріаційної і рівні кореням квадратів від діагональних елементів цієї матриці.

Аналогічно будуються інтервальні оцінки для функції регресії та індивідуального значення залежної змінної. Ці інтервали мають вигляд:

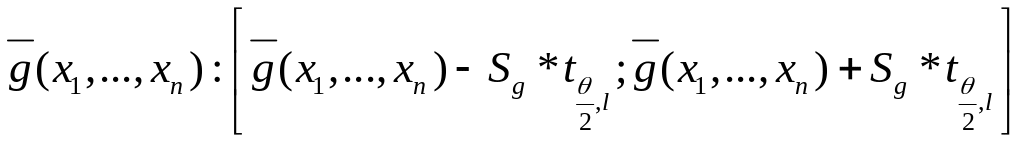- де

Для індивідуального значення довірчий інтервал має вигляд : 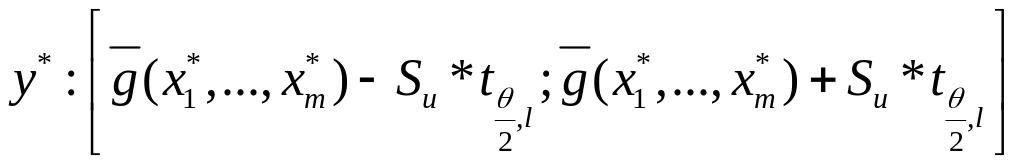- де

Крім, оцінок для параметрів функції та індивідуального значення на основі того ж самого принципу будуються також оцінки для дисперсії . Для цього використовують критерій Пірсона з ступенями вільності, тобто, двосторонній інтервал для дисперсії матиме вигляд: