22.Загальне понят про лінійну регресію. Оцінка парамет ліній регресії за допом методу найменших квадратів

Прості лінійні регрес моделі встановл лінійну залежність між двома змінними, одна з яких вважається залежною змінною (y) та розглядається як функція незалежної змінної (x).

У загал випадку проста лінійна регресійна модель має вигляд:

Y = α + β X + ε, де Y = {y1,…,yn} – вектор спостережень за залежною змінною, X = {x₁, …, x_n} – вектор спостережень за незалежною змінною, ε = {ε1, …, εn} – вектор випадкових величин (помилок), α, β – невідомі параметри регресійної моделі.

Щоб мати явний вигляд залежності Y = α + β X + ε, необхідно знайти α і β, а це можливо тільки тоді, коли відомі всі значення x та y (генеральна сукупність), проте характерною ознакою практичних задач з економетрії є відсутність генеральної сукупності x та y, тому у цій ситуації можна лише оцінити α і β на основі вибірки.

Якщо a, b – шукані оцінки α і β, то рівняння прямих ліній g(x) = α + βx,

назив відповід, теоретич та вибірковим рівнян лінійної регресії.

За міру відхилення теоретичної лінії регресії від вибіркової можна взяти, наприклад, одну з міри:

1. ; 2. ; 3. – МНК.

Недоліком міри 1 є те, що існує багато прямих, для яких вона є нульовою; міра 2 – нескрізь диференційована функція. Найбільш ефективною і теоретично обґрунтованою є міра 3, мінімізація якої (за параметрами a і b) становить суть методу найменших квадратів. Т ч за критерієм маємо:

– система нормальних рівнянь для визначення параметрів a і b;

b = ;

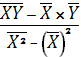a = .

23.Основні кореляційні характеристики: коваріація, коефіцієнт кореляції

Їх є 4: коваріац; коеф корел; коеф детермін; кореляц відношен.

(коваріац – хар-є наявність зв’язку між X та Y). Властивості: 1- 2- 3- 4- – незалежні між X,Y існує зв’язок , де – це варіація змінної X, – це варіація змінної Y.

Недоліки коваріації: залежить від розмірностей випад вел; не дозвол встановити силу зв’язку між X та Y, а лише його наяв.

(коеф корел – хар-є тісноту лінійного зв’язку між X та Y). Властивості: 1- ; 2- 3- , причому наближення до 1 свідчить про зростання тісноти лінійного зв’язку між X та Y; 4- немає лінійного зв’язку між X та Y, хоч будь-який інший може бути присутній; 5- пов’язані лінійною функціональною залежністю, тобто результати спостереження знаходяться на прямій лінії; 6- між X та Y існує прямий зв’язок, між X та Y існує обернений зв’язок.

(коеф детермінації – характеризує зв’язок між X та Y і адекватність моделі)

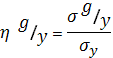, де

g( (кореляційне відношення – характеризує тісноту зв’язку як лінійного зв’язку, так і нелінійного)

Властивості: ; 2- X та Y – некорельовані ; 3- X та Y – пов’язані функціонально; 4- , причому у випадку лінійного зв’язку;

24.Основні передумови методу найменших квадратів. Теорема Гаусса-Маркова

Основні передумови МНК:

1-у моделі Y = X + X – детермінована величина, а Y та - випадкові величини;

2-математичне сподівання відхилення ;

3-дисперсія кожного випадкового відхилення є постійною і однаковою (D( ; виконання цього припущення називають гомоскедастичністю, а його невиконання – гетероскедастичністю);

4-відхилення та є некорельованими: M( ;

5-відхилення та є нормально розподіленою випадковою величиною.

При виконан припущень 1-5 модель Y = X + X назив класич нормал ліній регрес моделлю.

Теорема Гаусса-Маркова: якщо для регрес моделі Y = X + X викон припущення 1-5, то оцінки a, b, отримані за МНК, є:

1-точковими незміщеними оцінками M(a) = , M(b) = ;

2-точковими обґрунтованими оцінками ;

3-точковими ефективними оцінками, тобто мають найменшу дисперсію в класі лінійних незміщених оцінок.

25.Стандарт помилки регресії та коеф регресії. Відносні величини стандарт помилок коеф регресії та їх економ зміст. Крім оцінок a та b коефіцієнтів регресії, потрібно також оцінити випадкове відхилення , що не може бути визначені на основі вибірки. Оцінки теорет випад відхилен (помилки регресії) є відхиленнями (залишки регресії), що визначаються за формулою: .

Точковою незміщеною оцінкою дисперсії помилок регресії є величина .

Тоді стандарт помилкою регресії називають величину s = .

Дисперсії оцінок a та b обчислюють за формулами:

D(b)

D(a)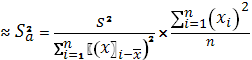

Стандарт помилками коефіцієнтів регресії називають величини: та .

З метою визначення якості точкових оцінок a та b обчислюють також выдносны величини стандартних похибок:

, .