4.2 Теорема подібності

Якщо точки деякої ланки утворюють геометричну фігуру , то на планах аналогів швидкості і прискорення утворюється подібна фігура . Для планів аналогів швидкості ці фігури повернуті на 90⁰.

Розглянемо кривошипно-повзунний механізм, у якого ланка 3 має конфігурацію трикутника (рисунок 4.10).

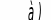
Рисунок 4.10 Рисунок 4.11

Рівняння для побудови плану аналогів швидкості точок :

Вектор перпендикулярний ОМ; вектор перпендикулярний вектор паралельний напрямній повзуна. Рівняння для точки N ланки 3:

Вектор перпендикулярний MN; вектор перпендикулярний NL. На побудованому плані аналогів швидкості (рисунок 4.11) утворюється трикутник , подібний до трикутника на плані механізму, оскільки сторони трикутників взаємно перпендикулярні. Обхід літер на плані механізму і на плані аналогів має збігатись.

Висновок: якщо деяка точка ділить ланку 6 на дві частини в деякому відношенні, то відповідна точка s на плані аналогів ділить відповідний ланці відрізок у такому ж відношенні.

На рисунку 4.10

Звідси визначається положення точки s на відрізку плану аналогів швидкості. Аналогічно знаходяться точки на плані прискорень.

4.4 Графічне диференціювання та інтегрування функцій

Якщо одна з кінематичних функцій задана у формі таблиці або графічно, то знайти похідну або інтеграл цієї функції в аналітичній формі складно.

У цьому випадку ефективними є методи графічного диференціювання та інтегрування функцій. Графічне диференціювання починають із побудови графіка функції за заданими значеннями у функції узагальненої координати або часу. Наприклад, заміряючи переміщення вихідної ланки механізму залежно від кута повороту вхідної ланки, одержуємо дані для побудови графіка (рисунок 4.12 а).

Рисунок 4.12

Графік будується в масштабах і . Розглянемо послідовність графічного диференціювання за методом хорд:

1. Точки кривої 1^/, 2^/, 3^/ … з’єднуються хордами.

2. З полюса р графіка 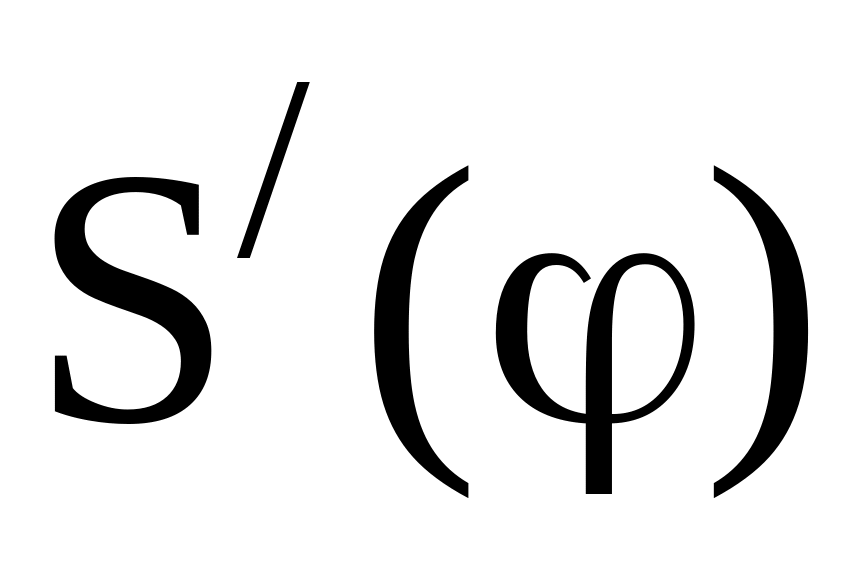проводяться промені паралельно проведеним хордам до перетину з віссю ординат.

3. Точки перетину проектуються на лінії, які ділять навпіл відрізки 0-1, 1-2, 2-3 …

Одержані на графіку точки 1^//, 2^//, 3^// … з’єднуються плавною кривою, яка показує зміну аналога швидкості. Визначимо масштаб діаграми . Розглянемо трикутник АВС (рисунок 4.12 а). За кут повороту з положення 1 у положення 2 ведена ланка перемістилась з положення В у положення С. З урахуванням масштабів аналог швидкості в інтервалі 1-2 дорівнює:

(1).

З графіка (рисунок 4.12 б)

(2). Враховуючи (1), (2), одержуємо:

м/мм. (4.36)

Графічне інтегрування за методом хорд проводиться в такій послідовності (рисунок 4.13).

На заданій діаграмі М(φ) у межах кожного відрізка 0-1, 1-2, 2-3 … знаходиться середнє значення моменту і знаходяться точки перетину з віссю ординат (рисунок 4.13 а). Точки перетину з’єднуються з полюсом променями. У межах відрізків 0-1, 1-2, 2-3 … на діаграмі (рисунок 4.13 б) паралельно відповідним променям, починаючи з першого відрізка, проводяться хорди – одержуємо точки 1^/, 2^/, 3^/ …, які об’єднуються плавною кривою. Одержана діаграма є інтегральною відносно вихідної діаграми.

Масштаб графіка :

Дж/мм, де , Нм/мм, , рад/мм – масштаби графіка ; Н, мм – полюсна відстань.

Рисунок 4.13