
- •Теорія механізмів та машин
- •Передмова
- •Завдання на курсову роботу з теорії механізмів і машин
- •Зміст курсової роботи
- •1. Аркуш 1. Проектування кулачкового механізму
- •2. Аркуш 2. Динамічне дослідження машини
- •3. Аркуш 3. Силовий аналіз машини
- •4. Розрахунок зубчатої передачі
- •5. Оформлення курсового проекту
- •І. Структурний аналіз механізмів
- •Іі. Синтез плоских механізмів з нижчими парами
- •2.1 Синтез кривошипно-повзунного механізму
- •2.2. Проектування схеми кулісного механізму з коливною кулісою за заданим ходом повзуна н і коефіцієнтом зміни середньої швидкості (рисунок 2.1)
- •2.4. Проектування схеми кулісного механізму за заданим коефіцієнтом зміни середньої швидкості, заданими розмірами і
- •Ііі. Аналоги швидкості і прискорення
- •IV Графічний метод визначення аналогів швидкостей та прискорень механізмів другого класу
- •4.1Розв’язання рівнянь аналогів швидкості
- •4.2 Теорема подібності
- •4.4 Графічне диференціювання та інтегрування функцій
- •V. Динамічне дослідження машин
- •Визначення мас та моментів інерції ланок механізму
- •5.1 Визначення зовнішніх навантажень ланок машин
- •Визначення сил тиску в циліндрах двигунів внутрішнього згорання та в поршневих компресорах.
- •Фази індикаторної діаграми
- •Фази індикаторної діаграми
- •Фази індикаторної діаграми
- •5.3 Вибір потужності асинхронного електродвигуна.
- •5.3.1. Визначення передавального числа, номінального момента:
- •5.3.2 Перевірка електродвигуна на працездатність.
- •5.4 Визначення моменту інерції маховика Момент інерції маховика
- •5.4.1 Розміри маховика
- •VI силове дослідження плоских важільних механізмів
- •6.1 Визначення інерційних сил і моментів
- •6.2 Метод кінетостатики
- •6.3 Сили взаємодії в кінематичних парах
- •6.4 Послідовність силового розрахунку
- •6.5 Методика силового розрахунку графоаналітичним способом
- •6.6 Важіль н.Є. Жуковського
- •VII Проектування евольвентної циліндричної зубчатої передачі
- •7.1. Загальні положення
- •7.2. Вибір коефіцієнтів зміщення
- •7.3. Евольвента, рівняння евольвенти в параметричній, векторній і координатній формах
- •7.4 Елементи та властивості евольвентного зачеплення
- •7.5 Розрахунок основних геометричних параметрів прямозубої евольвентної зубчатої передачі при заданій міжосьовій відстані аW
- •7.6 Розрахунок основних геометричних параметрів евольвентної зубчатої передачі при заданій кількості зубців коліс і міжосьовій відстані
- •VIII. Проектування кулачкових механізмів
- •8.1 Фазові кути
- •8.2 Закон руху веденої ланки
- •8.3 Вихідні дані для проектування
- •8.4 Визначення закону руху штовхача
- •8.5 Визначення основних розмірів кулачкових механізмів
- •8.6 Графічний метод профілювання кулачка
- •Позначення заданих параметрів механізмів для тем 1-18
- •Позначення заданих параметрів механізмів для тем 19-23
- •Види кулачкових механізмів
- •Закони руху вихідної ланки кулачкового механізму
- •Схеми редукторів
- •Тема 19. Дизель-повітрянодувна установка
- •Тема 20. Проектування та дослідження механізмів руху автомобіля
- •Тема 21. Проектування та дослідження поршневого компресора
- •Тема 22. Проектування та дослідження механізмів 4х-тактного двигуна
- •Тема 23. Проектування та дослідження механізмів двигуна і передачі мотоцикла
- •Література
7.3. Евольвента, рівняння евольвенти в параметричній, векторній і координатній формах

Рисунок 7.1
Евольвента утворюється при перекоченні
прямої
![]() по колу без ковзання точками прямої. В
зубчатих передачах як коло використовують
основне коло радіуса
по колу без ковзання точками прямої. В
зубчатих передачах як коло використовують
основне коло радіуса
![]() Кут профілю зуба
Кут профілю зуба
![]() утворюється між радіус-вектором т.К і
дотичною до профілю в точці К. Кут
утворюється між радіус-вектором т.К і
дотичною до профілю в точці К. Кут
![]() - це також кут між біжучим радіусом і
радіус-вектором точки К евольвенти. Кут
між початковим радіусом і радіус-вектором
- це також кут між біжучим радіусом і
радіус-вектором точки К евольвенти. Кут
між початковим радіусом і радіус-вектором
![]() називається евольвентним кутом
називається евольвентним кутом
![]() .
Кут між початковим радіусом і біжучим
радіусом позначимо
.
Кут між початковим радіусом і біжучим
радіусом позначимо
![]() радіальний кут (кут розгортки евольвенти)
радіальний кут (кут розгортки евольвенти)
![]() (7.2)
(7.2)
Коло є інволютою – траєкторією миттєвих
центрів обертання прямої. Тому
![]() є радіусом кривини евольвенти, він
дотичний до кола і перпендикулярний до
біжучого радіуса:
є радіусом кривини евольвенти, він
дотичний до кола і перпендикулярний до
біжучого радіуса:
![]() (7.3)
(7.3)
де
![]() в
радіанах.
в
радіанах.
Рівняння евольвенти в векторній формі:
![]() .
(7.4)
.
(7.4)
В матричній формі запису:
![]() (7.5)
(7.5)
де
![]() матриця
переходу від координатної системи
матриця
переходу від координатної системи
![]() до системи
до системи
![]() (рисунок 7.1).
(рисунок 7.1).
Вводимо допоміжний кут
![]() :
:
 (7.6)
(7.6)
 (7.7)
(7.7)
Перейдемо до координатної форми запису рівняння евольвенти:
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
![]()
![]() (7.10)
(7.10)
![]() (7.11)
(7.11)
При обертанні прямої
![]() проти годинникової стрілки (+)
утворюється ліва гілка евольвенти. При
(-) – права.
проти годинникової стрілки (+)
утворюється ліва гілка евольвенти. При
(-) – права.
За рисунком 7.1
![]() і за (9.3)
і за (9.3)
![]() з урахуванням (7.2):
з урахуванням (7.2):
![]() (7.12)
(7.12)
![]() .
(7.13)
.
(7.13)
(7.12), (7.13) – рівняння евольвенти в параметричній формі. Для евольвентної функції inv складена таблиця для визначення через .
7.4 Елементи та властивості евольвентного зачеплення
При зачепленні двох зубчатих коліс встановлюються певні співвідношення між елементами кожного зубчатого колеса.
7.4.1 Радіуси ділильних кіл:
![]()
![]()
7.4.2 Радіуси основних кіл:
![]()
![]()
де
![]() кут
головного профілю стандартної рейки.
кут
головного профілю стандартної рейки.
7.4.3 Радіуси початкових кіл:
![]()
де
![]() кут зачеплення. Кут зачеплення
утворюється між спільною дотичною до
кут зачеплення. Кут зачеплення
утворюється між спільною дотичною до
основних кіл коліс і перпендикуляром до прямої, що з’єднує центри коліс.
7.4.4 Міжосьова відстань аW:
![]()
![]()
Кути і W однакові при нульовому і рівнозміщеному зачепленні. При визначенні Z1 округлення до цілого проводити в сторону збільшення. При заданих Z1, Z2, т за рахунок зміни кута зачеплення одержують точну міжосьову відстань в допустимих межах зміни кута.
7.4.5 Радіуси кола головок:
![]()
![]()
Необхідна перевірка на загострення зубців.
7.4.6 Радіуси кола западин:
![]()
![]() .
.
Необхідно проводити перевірку наявності достатнього зазору між колом головок одного колеса і колом западин другого. Рекомендується радіуси кола головок визначити:
![]()
7.4.7 Товщина зубців шестерні і колеса по ділильних колах:
![]()
![]()
де
![]() відповідні коефіцієнти зміщення.
відповідні коефіцієнти зміщення.
7.4.8 Кроки на ділильному, основному, початковому колах:
![]()
![]()
![]()
![]()
![]()
![]()
де S1,2 , Sb1,2 , SW1,2 - товщини зубців передачі на ділильному, основному, початковому колах коліс відповідно;
S31,2 , S3b1,2 , S3W1,2 – ширина западин на ділильному, основному і початковому колах коліс відповідно.
7.4.9 Евольвентні кути:
- кут між осями 01У01, 02У02 і радіус-векторами точок евольвент, що лежить на ділильних колах коліс (рисунок 7.2).
![]() відповідає
відповідає
![]()
![]() кут загострення головок зубчатих коліс
в координатах
кут загострення головок зубчатих коліс
в координатах
![]()
![]() відповідно.
відповідно.
W – кут між осями 01У01, 02У02 і радіус-векторами полюса зачеплення P;
![]() кут між осями 01У01, 02У02
і радіус-векторами точок евольвент, що
знаходяться на колі головок зубчатих
коліс;
кут між осями 01У01, 02У02
і радіус-векторами точок евольвент, що
знаходяться на колі головок зубчатих
коліс;
кути
W ,
![]() визначаються через відповідні кути W
, a1,2.
визначаються через відповідні кути W
, a1,2.

Рисунок 7.2
7.4.10 Радіальні кути:
 - радіальний кут між осями 01У01,
02У02 і радіусами rb1,2,
які перпендикулярні спільній дотичній
до основних кіл зубчатих коліс (радіуси
01N1, 02N2 на рисунку
7.2).
- радіальний кут між осями 01У01,
02У02 і радіусами rb1,2,
які перпендикулярні спільній дотичній
до основних кіл зубчатих коліс (радіуси
01N1, 02N2 на рисунку
7.2).
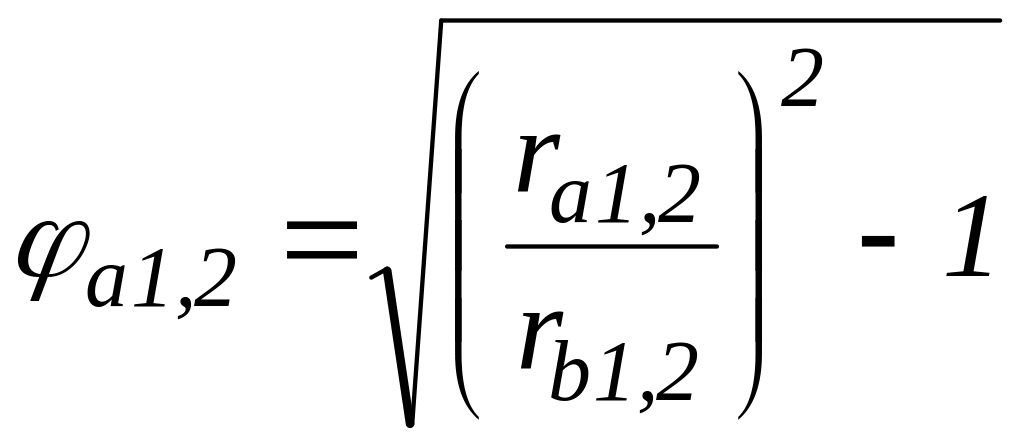 - радіальні кути головок, що відповідають
положенню точок евольвент на колах
головок коліс. Інакше, кути між осями
01У01, 02У02 і
радіусами, які перпендикулярні дотичним
до основних кіл коліс, проведених з
точок а1, а2 на рисунку 7.2.
- радіальні кути головок, що відповідають
положенню точок евольвент на колах
головок коліс. Інакше, кути між осями
01У01, 02У02 і
радіусами, які перпендикулярні дотичним
до основних кіл коліс, проведених з
точок а1, а2 на рисунку 7.2.
7.4.11 Лінія зачеплення:
g- теоретична довжина лінії зачеплення
- відстань на спільній дотичній до
основних кіл між точками N1 ,N2
, точками дотику. Цим точкам відповідає
радіальний кут
![]()
![]() довжина активної лінії зачеплення –
відстань на теоретичній лінії зачеплення
між точками перетину цієї лінії з колами
головок (точки К1,К2) зубчатих
коліс. Зачеплення зубців здійснюється
в межах g для
зубчатих передач зовнішнього зачеплення.
довжина активної лінії зачеплення –
відстань на теоретичній лінії зачеплення
між точками перетину цієї лінії з колами
головок (точки К1,К2) зубчатих
коліс. Зачеплення зубців здійснюється
в межах g для
зубчатих передач зовнішнього зачеплення.
![]() .
(7.14)
.
(7.14)
7.4.12 Радіуси кривини евольвенти
Радіуси кривини евольвенти визначаються за формулою (7.3). Довжина радіусів кривини евольвент в точках контакту змінюється з поворотом зубчатих коліс, але їх сума залишається сталою і дорівнює g – довжині теоретичної лінії зачеплення:
![]() .
(7.15)
.
(7.15)
Радіуси кривини евольвенти в полюсі зачеплення:
![]()
![]()
![]()
Радіус кривини евольвенти шестерні (першого колеса) від полюса до кола головок збільшується, а радіус кривини евольвенти колеса (другого колеса) від полюса до основного кола зменшується:
![]() ,
(7.16)
,
(7.16)
де
![]() – радіус кривини евольвенти шестерні
в межах від W1
до а1;
– радіус кривини евольвенти шестерні
в межах від W1
до а1;
![]() – радіус кривини евольвенти колеса в
межах від W2
до a2.
– радіус кривини евольвенти колеса в
межах від W2
до a2.
При зміні радіального кута шестерні в межах :
![]() ,
,
![]()
![]() (7.17)
(7.17)
При зміні радіального кута колеса в межах:
![]() ,
,
![]()
![]() .
(7.18)
.
(7.18)
7.4.13 Коефіцієнт перекриття:
![]() (7.19)
(7.19)
де
![]() довжина дуги початкового кола, по якій
перемістилась точка профілю зубця за
час зачеплення однієї пари зубців;
довжина дуги початкового кола, по якій
перемістилась точка профілю зубця за
час зачеплення однієї пари зубців;
![]() крок початкового кола.
крок початкового кола.
Крок і довжина дуги основного кола
пропорційні, відповідно, кроку і довжині
дуги початкового кола. Довжина
![]() (відрізок К1 – К2 на лінії
зачеплення) дорівнює довжині дуги
основного кола за час зачеплення,
оскільки перекочування відбувається
без ковзання. Коефіцієнт перекриття
враховує плавність і безперервність
зачеплення передачі. Для евольвентної
прямозубої передачі:
(відрізок К1 – К2 на лінії
зачеплення) дорівнює довжині дуги
основного кола за час зачеплення,
оскільки перекочування відбувається
без ковзання. Коефіцієнт перекриття
враховує плавність і безперервність
зачеплення передачі. Для евольвентної
прямозубої передачі:
![]()
