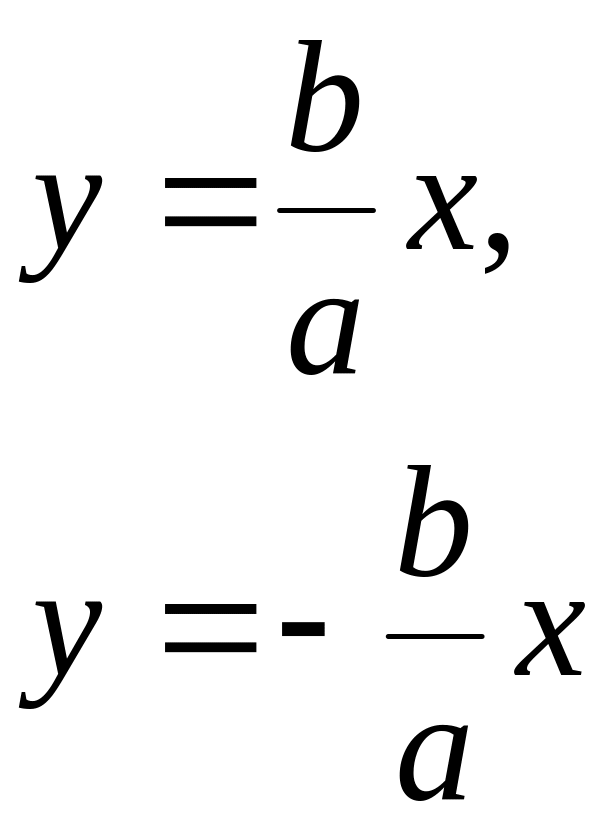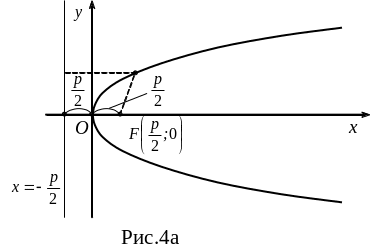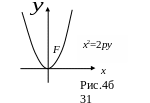- •Высшая математика
- •Содержание
- •Глава I. Элементы линейной алгебры
- •§1.1. Матрицы и определители
- •§1.2. Системы m линейных алгебраических уравнений с m неизвестными
- •1.3. Операции над матрицами
- •1.4. Обратная матрица. Матричные уравнения и системы линейных уравнений
- •Решение систем линейных уравнений с помощью обратной матрицы
- •1.5. Собственные числа и собственные векторы матрицы
- •Глава 2. Векторная алгебра
- •§2.1 Векторы. Линейные операции над векторами
- •§2.2. Скалярное произведение
- •Свойства скалярного произведения
- •§2.3. Векторное произведение векторов
- •Свойства векторного произведения
- •§2.4. Смешанное произведение трех векторов
- •Глава III. Аналитическая геометрия
- •§ 3.1. Прямая линия на плоскости
- •Угол между двумя прямыми
- •Расстояние от точки до прямой
- •§ 3.2. Кривые второго порядка на плоскости
- •§ 3.3. Общее уравнение кривых второго порядка Преобразование уравнения кривой второго порядка к каноническому виду
- •§ 3.4. Плоскость в пространстве
- •§ 3.5. Прямая в пространстве. Прямая и плоскость
- •Глава IV. Математический анализ
- •§4.1. Основные элементарные функции, некоторые свойства и графики
- •§4.2. Предел функции. Замечательные пределы. Непрерывность функции
- •Замечательные пределы
- •Непрерывность функции
- •Разрывы функции
- •§4.3. Дифференцирование функций. Основные формулы дифференцирования
- •Основные правила дифференцирования
- •§4.4. Уравнения касательной и нормали к плоской кривой
- •§4.5. Производные высших порядков. Правила Лопиталя
- •Правила Лопиталя
- •§4.6. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке
- •§4.7. Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты
- •§4.8. Параметрически заданные функции. Векторная функция скалярного аргумента. Кривизна плоской кривой
- •Список рекомендуемой литературы
§ 3.2. Кривые второго порядка на плоскости
Уравнение вида Ах2+2Вху+Су2+2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
В табл. 3 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
Таблица 3
№ п/п |
Определение кривой |
Вид уравнения |
Примечание |
1 |
Э
|
|
2а – большая ось; 2b – малая ось 2с–межфокус-ное; расстояние с2=а2-b2;
Т. А1,А2,В1,В2 – вершины эллипса |
№ п/п |
Определение кривой |
Вид уравнения |
Примечание |
2 |
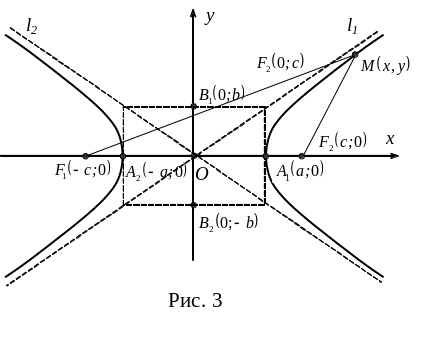
Гипербола – множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (рис.3)
|
|
2а–действи-тельная ось; 2b–мнимая ось; 2с –меж-фокусное расстояние с2=а2+b2; - эксцентри-ситет, >1. Точки А1,А2 – вершины гиперболы.
Прямые
- асимптоты |
3. |
Парабола - множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
|
у2=2px – каноническое уравнение параболы, симметричной относительно оси ОХ
x2=2pу – каноническое уравнение параболы, симметричной относительно оси ОY (рис.4б) |
F
Точка (0;0) – вершина параболы (рис.3а)
F
Точка (0;0) – вершина параболы (рис.4б) |
______________
3.2.1. Найти координаты
фокусов и эксцентриситет эллипса
![]() .
Построить эллипс.
.
Построить эллипс.
3.2.2. Составить
каноническое уравнение эллипса, у
которого а) большая полуось равна 10,
эксцентриситет равен 0,8; б) малая полуось
равна
![]() ,
расстояние между фокусами равно 8.
,
расстояние между фокусами равно 8.
3.2.3. Эллипс,
симметричный относительно осей координат,
проходит через точки М(2;![]() )
и В(0;2). Написать его уравнение. Построить
кривую.
)
и В(0;2). Написать его уравнение. Построить
кривую.
3.2.4. Построить гиперболу х2-4у2=16 и ее асимптоты. Найти фокусы, эксцентриситет, угол между асимптотами.
3.2.5. Написать
каноническое уравнение гиперболы, зная,
что: а) расстояние между фокусами
равно 10, между вершинами равно 8; б)
вещественная полуось равна
![]() ,
эксцентриситет равен
,
эксцентриситет равен
![]() .
.
3.2.6. Написать
уравнение гиперболы, имеющей вершины
в фокусах, а фокусы – в вершинах эллипса
![]() .
.
3.2.7. Написать
уравнения прямых, проходящих через
левую вершину гиперболы
![]() 1
а) параллельно прямой 3х-2у+6=0;
б) перпендикулярно асимптоте, образующей
острый угол с осью ОХ.
1
а) параллельно прямой 3х-2у+6=0;
б) перпендикулярно асимптоте, образующей
острый угол с осью ОХ.
3.2.8. Парабола с вершиной в начале координат проходит через точку А(2;4) и симметрична относительно оси ОХ. Написать ее уравнение.
3.2.9. Написать каноническое уравнение эллипса, зная, что его большая полуось а=12, эксцентриситет равен 0,5. Найти расстояние между фокусами.
3.2.10. Определить полуоси, координаты фокусов, эксцентриситет эллипса 3х2+4у2-12=0.
3.2.11. Написать
уравнение прямой, проходящей через
нижний правый фокус эллипса
![]() под
углом 45
к оси ОХ.
под
углом 45
к оси ОХ.
3.2.12. Определить
фокусы, вершины, эксцентриситет и
асимптоты гиперболы
![]() .
Сделать эскиз.
.
Сделать эскиз.
3.2.13. Написать каноническое уравнение гиперболы, проходящей через точки А(2;1), В(-4; 7).
3.2.14. Написать
уравнение прямой, проходящей через
левую вершину гиперболы
![]() и отсекающую от
оси ОY
отрезок 5 единиц.
и отсекающую от
оси ОY
отрезок 5 единиц.
3.2.15. Парабола с вершиной в начале координат проходит через точку А(1;-2) и симметрична относительно оси ОY. Написать уравнение параболы, найти координаты фокуса и уравнение директрисы.

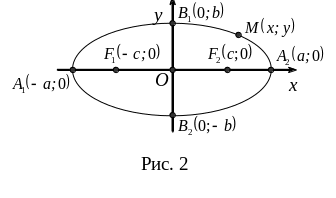 ллипс
– множество всех точек плоскости,
сумма расстояний от которых до двух
точек, называемых фокусами,
есть величина постоянная (рис.2)
ллипс
– множество всех точек плоскости,
сумма расстояний от которых до двух
точек, называемых фокусами,
есть величина постоянная (рис.2)