Свойства операций над событиями

Поскольку случайные события рассматриваются как множества, определенные на пространстве элементарных исходов , очевидно, что алгебраические свойства случайных событий вытекают из соответствующих свойств множеств:

Приведенный список не исчерпывает всех свойств операций над событиями. В то же время из него видно, что основные действия над событиями, в частности, операции сложения (объединения) и умножения (пересечения), в определенном смысле аналогичны сложению и умножению чисел. Эти операции обладают свойствами коммутативности, ассоциативности и дистрибутивности. Для операции умножения событий роль, аналогичную роли единицы и нуля при умножении чисел, выполняют, соответственно, множества и . Вместе с тем, теоретико–множественные равенства 6, 6 и им подобные показывают, что полной аналогии нет.

Алгебра и сигма-алгебра событий

В случае конечной или счетной теоретико-вероятностной схемы в качестве события рассматривается любое подмножество конечного или счетного пространства элементарных событий . Если же пространство непрерывно, то имеет место континуум элементарных исходов. Попытка считать событием любое подмножество непрерывного пространства сопряжена с большими трудностями.

Поэтому в общем случае приходится иметь дело не со всеми подмножествами пространства , а лишь с определенным классом, замкнутым относительно операций суммы, произведения и дополнения.

Предположим, что является пространством всех элементарных исходов для какого-нибудь случайного эксперимента, каждому результату которого соответствует ровно одна точка из , а разным результатам соответствуют разные точки. Выделим некоторую совокупность случайных событий , определенных на пространстве элементарных исходов . Другими словами, выделим совокупность подмножеств множества . Причем, наложим условие, что содержит как случайные события , так и события, полученные в результате применения любой из описанных операций к любым элементам системы.

Совокупность случайных событий , определенных на пространстве элементарных исходов , называется алгеброй или булевой алгеброй – по имени английского математика Дж. Буля (1815 – 1864), если выполнены следующие условия:

1. (алгебра событий содержит достоверное событие);

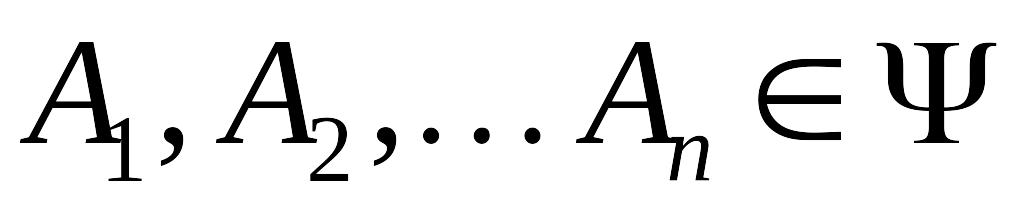2. Если , то 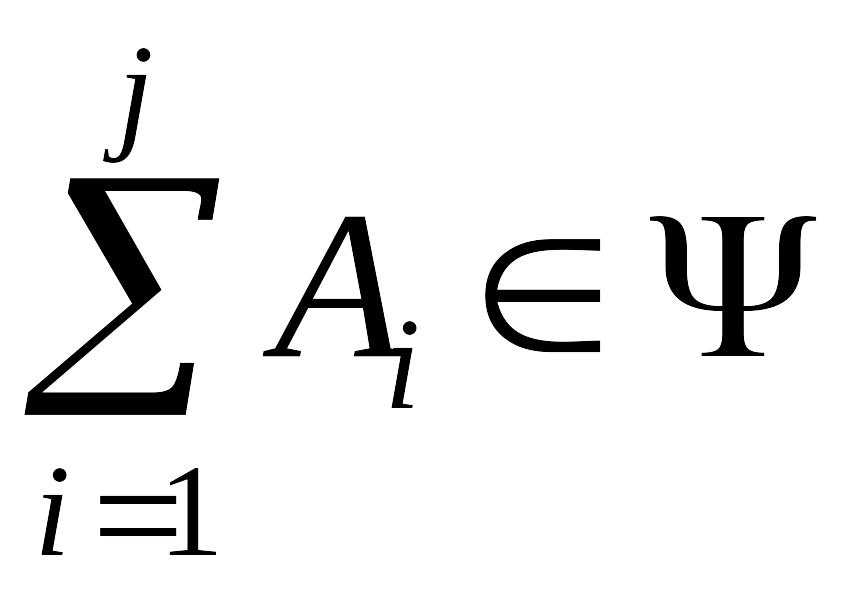для любых 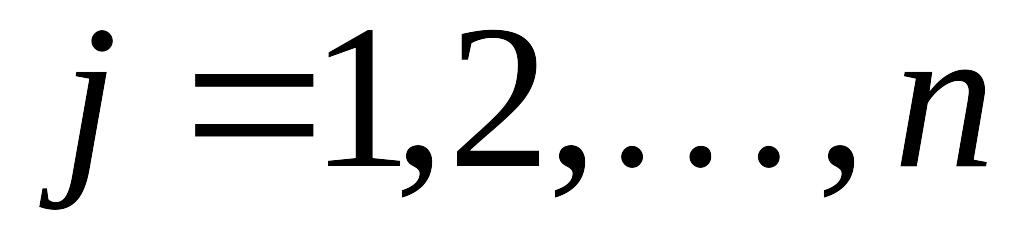(вместе с любым конечным набором событий алгебра содержит и их сумму);

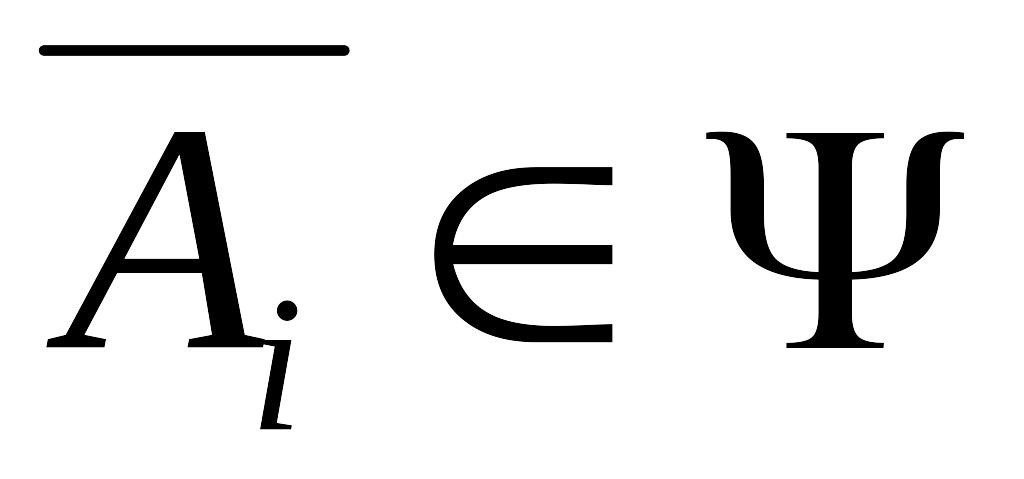3. Если , то (вместе с любым событием алгебра содержит противоположное событие).

Можно показать, в частности, что: , если и , то:

• ;

• .

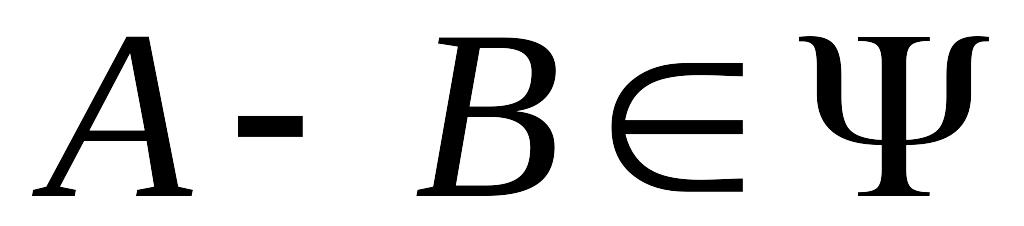Другими словами, оказывается, что условий 1 – 3 достаточно для того, чтобы любое конечное число других операций над случайными событиями не выводило бы нас за пределы алгебры . Таким образом, алгебра множеств – это система подмножеств некоторого множества , замкнутая относительно операций суммы (объединения), произведения (пересечения) и дополнения.

Очевидно, что одно и то же множество порождает различные алгебры. Самая «бедная» алгебра состоит из двух множеств – пустого множества и множества :

.

В понятиях теории вероятностей это соответствует невозможному и достоверному событиям. Любое подмножество порождает четырехэлементную алгебру:

Для экспериментов с конечным числом исходов множество–степень множества , т.е. совокупность всех подмножеств , включающая пустое множество , составляет алгебру , причем это самая «богатая» алгебра, порождаемая множеством . Поэтому для таких экспериментов любое подмножество множества может интерпретироваться как наблюдаемое событие, а все события, связанные с пространством элементарных исходов , образуют алгебру наблюдаемых случайных событий.

Под наблюдаемым событием понимается такое подмножество множества , которое одновременно принадлежит и булевой алгебре . Таким образом, класс наблюдаемых в данном эксперименте событий, вообще говоря, ỳже класса всех подмножеств множества . Если, например, , но , то событие по определению не наблюдаемо в данном эксперименте. Такое определение наблюдаемого события согласуется с введенным ранее эмпирическим понятием случайного события, как наблюдаемого результата эксперимента.

При рассмотрении многих задач теории вероятностей приходится иметь дело и с бесконечным числом операций. Для того, чтобы можно было рассматривать бесконечное число операций над событиями, необходимо усилить ограничения, налагаемые на алгебру .

Система подмножеств множества , называется -алгеброй, а соответствующее множество событий  борелевским, если она удовлетворяет следующим условиям:

1. (–алгебра событий содержит достоверное событие);

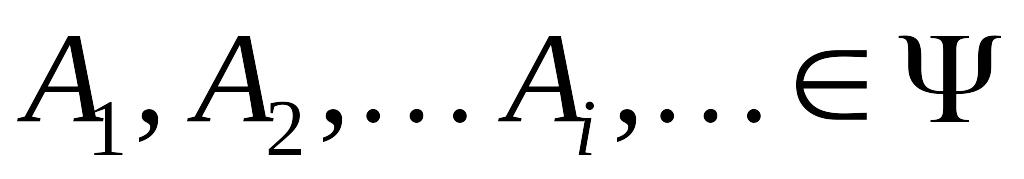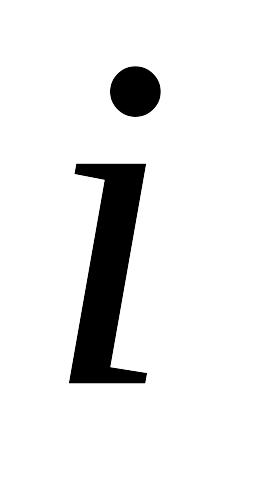
2. Если , то для любых 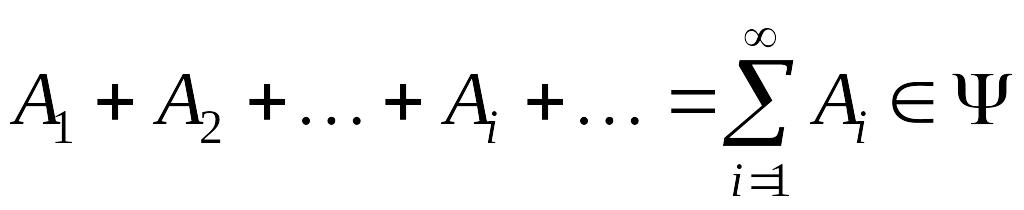(вместе с любым конечным или счетным набором событий –алгебра содержит и их сумму);

3. Если , то (вместе с любым событием –алгебра содержит противоположное событие).

Условие 2 для алгебры является следствием условия 2 для –алгебры, поэтому требования для –алгебры более сильные.

Используя условие 3 и равенство 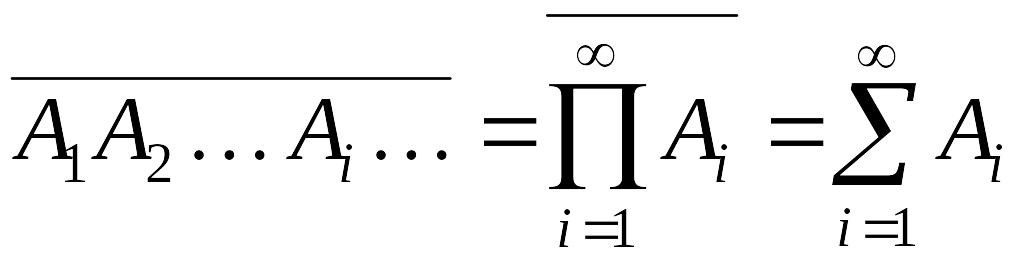, легко убедиться в справедливости следующего утверждения.

Пусть – –алгебра. Тогда, если , то для любых .

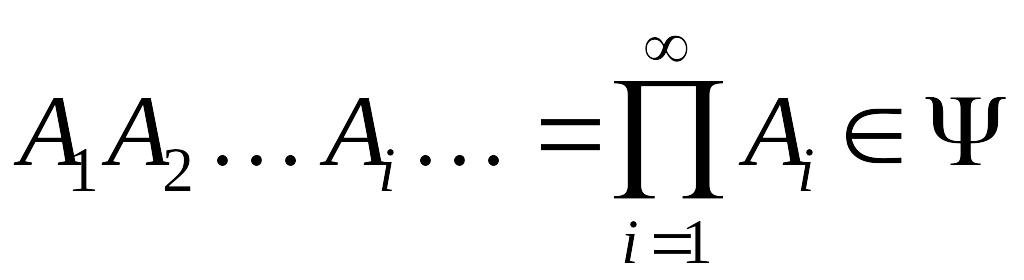Таким образом, счетное число операций суммирования или перемножения событий не выводит за пределы –алгебры.

Вообще говоря, действия над событиями важны не сами по себе, а как средство определения вероятностей одних событий через вероятности других событий. Далее будет введена вероятность случайного события как функция, заданная на подмножествах пространства . Прежде, чем определять эту функцию, следует задать область определения этой функции. Поскольку эта функция задается для всех наблюдаемых событий, связанных с пространством элементарных исходов , то функция должна быть определена на системе подмножеств пространства , которая является –алгеброй. Поэтому разумно поставить следующее условие: если известны вероятности событий и , то должны быть определены правила вычисления вероятностей событий , , а также вероятности противоположных событий и .