Совместная функция распределения двумерной случайной величины
Пусть
– пара действительных чисел. Обозначим
вероятность события
,
состоящего в том, что
примет значение меньшее
,
и при этом
примет значение меньшее
,
обозначим через
.
Если и будут меняться, то, в общем случае, будет изменяться и , т.е. есть функция от и .
Функция , определяющая для каждой пары чисел вероятность того, что примет значение меньшее , и при этом примет значение меньшее , называется совместной функцией распределения двумерной случайной величины (безразлично, дискретной или непрерывной):
= .
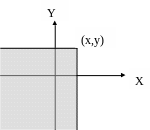
Геометрически
это равенство можно истолковать так:
– это вероятность того, что случайная
точка (
)
попадет в бесконечный квадрант с вершиной
(
),
расположенный левее и ниже этой вершины.
Свойства совместной функции распределения двумерной случайной величины
1. Значения совместной функции распределения удовлетворяют двойному неравенству:
.
2. – неубывающая функция по каждому аргументу, т.е.
,
если
;
,
если
.
3. Совместная функция распределения имеет следующие предельные значения:
;
;
;
.
4. При
совместная функция распределения
системы становится функцией распределения
составляющей
:
;
при
совместная функция распределения
системы становится функцией распределения
составляющей
:
.
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
Непрерывную двумерную случайную величину, которая описывается непрерывной совместной функцией распределения , имеющей непрерывные (за исключением, быть может, конечного числа точек), частные производные второго порядка, можно задать, пользуясь плотностью распределения.
Плотность
совместного распределения вероятностей
непрерывной двумерной случайной величины
(
,
)
– это вторая смешанная частная производная
от функции распределения
:
.
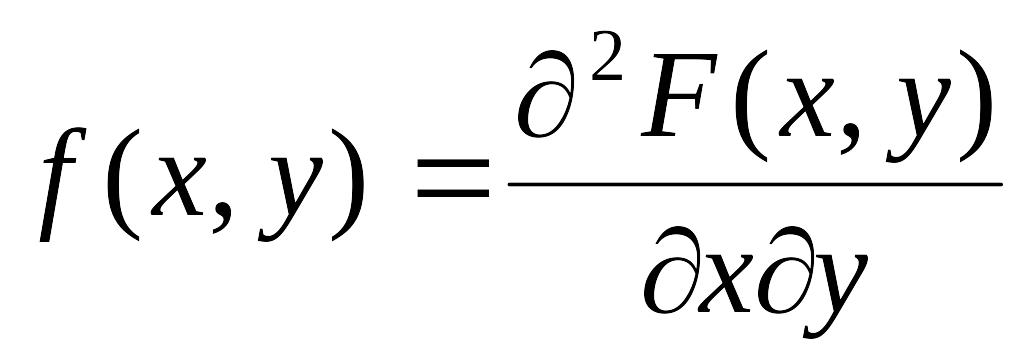Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
Зная плотность совместного распределения , можно найти функцию распределения по формуле:
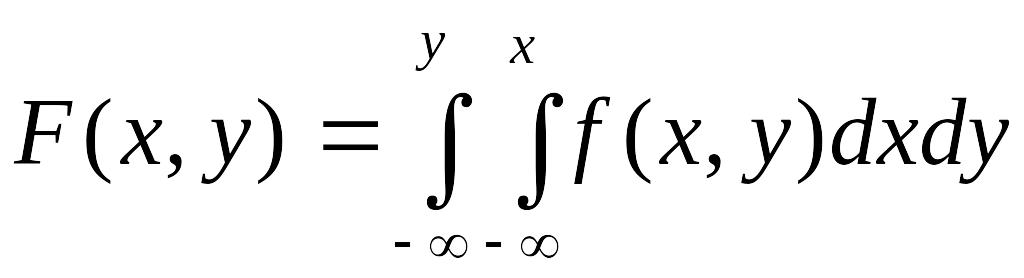
что непосредственно следует из определения плотности распределения двумерной непрерывной случайной величины ( , ).
Плотность
совместного распределения вероятностей
можно рассматривать как предел отношения
вероятности попадания случайной точки
в прямоугольник (с вершиной в точке
и сторонами
и
)
к площади этого прямоугольника, когда
обе стороны этого прямоугольника
стремятся к нулю.
Действительно,
вероятность попадания случайной точки
(
,
)
в прямоугольник с вершинами
,
,
и
равна:
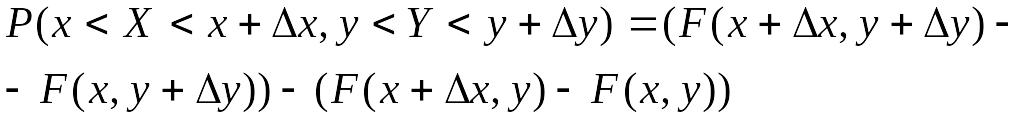
Применив к правой части теорему Лагранжа, получим:
где
;
.
Отсюда:
.
Приняв
во внимание, что
– площадь рассматриваемого прямоугольника,
можно сделать вывод, что
– это отношение вероятности попадания
случайной точки в рассматриваемый
прямоугольник к площади этого
прямоугольника. Если перейти к пределу
при
и
,
то
и
и, следовательно,
.
Аналогично вероятности для дискретной
случайной величины, плотность распределения
вероятности для непрерывных величин
можно представить в виде:
.
Свойства двумерной плотности вероятности
Двумерная плотность вероятности неотрицательна:
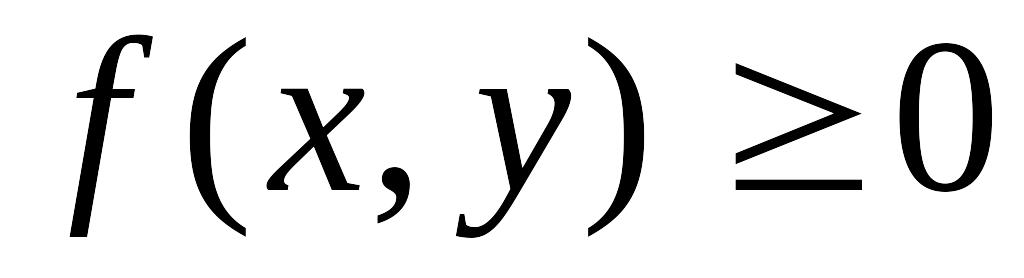.Двойной несобственный интеграл с бесконечными пределами от двумерной плотности вероятности равен единице:
.
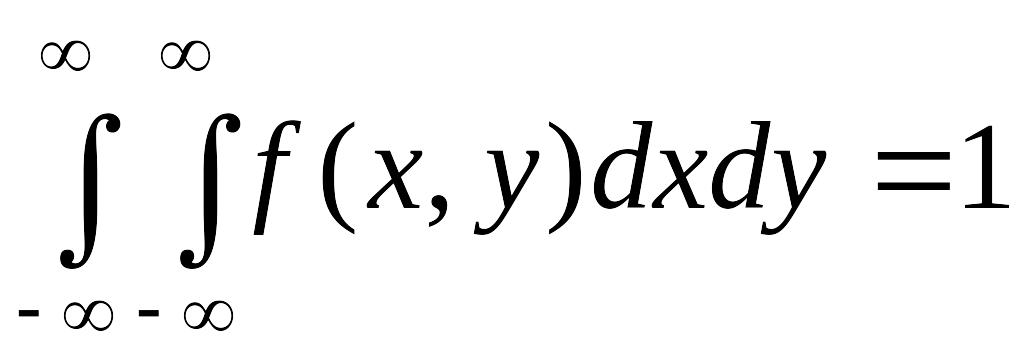