
- •Тема 1. Вероятностные пространства 30
- •Тема 2. Основные вероятностные схемы испытаний 60
- •Тема 3. Случайные величины 87
- •Тема 4. Математическая статистика 140
- •Введение Место теории вероятностей и математической статистики в современной математической науке и их роль в экономических исследованиях
- •Особенности изучения теории вероятностей и математической статистики менеджером
- •Краткие сведения
- •Тема 1. Вероятностные пространства Лекция 1. Пространство случайных событий
- •Основные понятия теории вероятностей
- •Случайные события
- •Понятие случайного эксперимента
- •Пространство элементарных событий
- •Наступление события, благоприятствующие исходы
- •Совместные (совместимые), несовместные (несовместимые) события
- •Достоверное и невозможное события
- •Алгебра событий Операции над событиями (сумма, разность, произведение)
- •Свойства операций над событиями
- •Алгебра и сигма-алгебра событий
- •Общее определение вероятности
- •Классическое определение вероятности события. Случаи равновероятных исходов
- •Статистическое определение вероятности события. Случаи неравновероятных исходов
- •Геометрические вероятности
- •Аксиоматическое построение теории вероятностей
- •, Т.Е. Вероятность достоверного события равна единице;
- •Вероятность события , заключающееся в том, что наступит одно из попарно несовместных событий ( ), составляет
- •Полная группа событий
- •Условная вероятность
- •Формула умножения вероятностей
- •Формула сложения вероятностей
- •Независимость событий
- •Простейшие свойства вероятностей
- •Свойства условных вероятностей
- •Формула полной вероятности. Формула Байеса
- •Контрольные вопросы к теме №1
- •Тема 2. Основные вероятностные схемы испытаний Лекция 2. Основные формулы вычисления вероятностей
- •Классическая вероятностная схема
- •Правила суммы и произведения
- •Схемы выбора. Основные понятия комбинаторики
- •Выбор без возвращения, с учетом порядка
- •Выбор без возвращения, без учета порядка
- •Выбор с возвращением и с учетом порядка
- •Выбор с возвращением и без учета порядка
- •Урновая схема
- •Наивероятнейшее число наступления событий в схеме Бернулли
- •Предельные теоремы для схемы Бернулли
- •Локальная теорема Муавра–Лапласа
- •Интегральная теорема Муавра – Лапласа
- •Теорема Пуассона
- •Понятие потока событий
- •Полиномиальная схема
- •Понятие цепи Маркова
- •Однородные цепи Маркова
- •Равенство Маркова
- •Предельные вероятности
- •Контрольные вопросы к теме №2
- •Тема 3. Случайные величины Лекция 3. Одномерные случайные величины
- •Непрерывные и дискретные случайные величины
- •Закон распределения случайной величины
- •Функция распределения случайной величины и ее свойства
- •Свойства функции распределения
- •Числовые характеристики непрерывных случайных величин Математическое ожидание случайной величины, его вероятностный смысл и свойства
- •Свойства математического ожидания
- •Дисперсия случайной величины и ее свойства
- •Среднеквадратическое отклонение
- •Начальные и центральные моменты
- •Основные примеры распределений дискретной случайной величины
- •Биномиальное распределение, его математическое ожидание, дисперсия
- •Распределение Пуассона
- •Геометрическое распределение
- •Непрерывные случайные величины Функция и плотность распределения вероятностей
- •Числовые характеристики непрерывных случайных величин
- •Основные примеры распределений непрерывной случайной величины Равномерное распределение
- •Показательное распределение
- •Нормальное распределение
- •Свойства функции Гаусса
- •Центральная предельная теорема
- •Вероятность попадания нормальной случайной величины в заданный интервал
- •Функция Лапласа и ее свойства
- •Вычисление вероятности заданного отклонения. Правило «трех сигм»
- •Лекция 4. Многомерные случайные величины
- •Закон распределения вероятностей двумерной случайной величины
- •Совместная функция распределения двумерной случайной величины
- •Свойства совместной функции распределения двумерной случайной величины
- •Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
- •Свойства двумерной плотности вероятности
- •Условное математическое ожидание
- •Независимые случайные величины
- •Числовые характеристики системы двух случайных величин
- •Корреляционный момент
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Линейная регрессия. Метод наименьших квадратов
- •Распределение 2
- •Распределение Стьюдента
- •Распределение Фишера
- •Предельные теоремы теории вероятностей Закон больших чисел. Неравенство Чебышева. Теорема Чебышева
- •Контрольные вопросы к теме №3
- •Тема 4. Математическая статистика Лекция 5. Основы математической статистики
- •Выборочный метод и его основные понятия
- •Способы отбора
- •Вариационный ряд для дискретных и непрерывных случайных величин
- •Полигон и гистограмма
- •Эмпирическая функция распределения и ее свойства
- •Свойства эмпирической функции распределения
- •Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок
- •Выборочные среднее и дисперсия
- •Надежность и доверительный интервал
- •Определение доверительных интервалов Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
- •Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
- •Доверительный интервал для оценки среднего квадратического отклонения нормального распределения
- •Проверка статистических гипотез
- •Статистический критерий
- •Критическая область. Область принятия гипотезы. Критические точки
- •Критерий согласия Пирсона о виде распределения
- •Элементы теории корреляции
- •Выборочные уравнения регрессии
- •Линейная регрессия
- •Множественная линейная регрессия
- •Нелинейная регрессия
- •Логарифмическая модель
- •Обратная модель
- •Степенная модель
- •Показательная модель
- •Цепи Маркова Цепи Маркова с дискретным временем
- •Однородные цепи Маркова
- •Переходные вероятности. Матрица перехода
- •Равенство Маркова
- •Цепи Маркова с непрерывным временем
- •Уравнения Колмогорова
- •Финальные вероятности состояний системы
- •Предельные вероятности
- •Контрольные вопросы к теме №4
- •Экзаменационные вопросы
- •Литература
- •Теория вероятностей и математическая статистика
- •Технический редактор т.В. Жибуль
- •220007, Г. Минск, ул. Московская, 17.
Линейная регрессия. Метод наименьших квадратов
Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Если имеется некоторое множество точек наблюдений, через него всегда можно попытаться провести такую прямую линию, которая является наилучшей в определенном смысле среди всех прямых линий, то есть «ближайшей» к точкам наблюдений по их совокупности. Для этого нужно вначале определить понятие близости прямой к некоторому множеству точек на плоскости. Меры такой близости могут быть различными. Однако любая разумная мера должна быть, очевидно, связана с расстояниями от точек наблюдений до рассматриваемой прямой линии.
Рассмотрим
двумерную случайную величину
![]() .
Предположим, что некоторая величина
.
Предположим, что некоторая величина
![]() приближенно представляет величину
и может быть записана как функция от
в виде линейной зависимости
приближенно представляет величину
и может быть записана как функция от
в виде линейной зависимости
![]() ,
где
и
,
где
и
![]() – неизвестные параметры.
– неизвестные параметры.
Требуется
так подобрать параметры
и
,
чтобы функция
![]() была наилучшим приближением к случайным
значениям
.
была наилучшим приближением к случайным
значениям
.
В
качестве меры отклонения величины
от значений
можно взять математическое ожидание
квадрата разности (
–
),
т.е.
![]() .
.
Минимизация
этого выражения позволяет получить
соотношения для определения параметров
и
.
Полученную таким образом функцию
![]() называют наилучшим приближением
по методу наименьших квадратов, а функцию
называют наилучшим приближением
по методу наименьших квадратов, а функцию
![]() называют линейной средней квадратической
регрессией
на
.
называют линейной средней квадратической
регрессией
на
.
Теорема. Линейная средняя квадратическая регрессия на имеет вид:

где
![]() ,
,
![]() ,
,
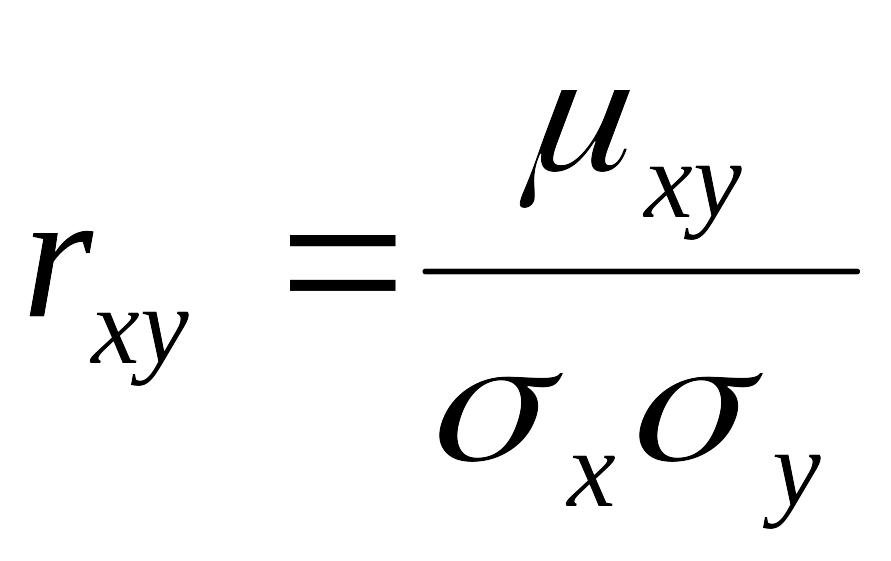 ,
,
![]() ,
,
![]() .
.
Доказательство:
Пусть
.
Рассмотрим функцию
![]() .
.
Поскольку:
![]() ,
,
![]() ,
,
тогда, раскрывая квадрат разности, получим:
![]()
![]()
![]()
Так как
![]() ,
то
,
то
![]() ,
а из равенства
,
а из равенства
![]() следует
.
следует
.
Кроме
того,
![]() .
.
Откуда
следует, что
![]() .
.
Подставив
полученные выражения, получим:
![]()
![]() .
.
На основании необходимого условия экстремума функции двух переменных ее частные производные по соответствующим переменным должны быть равны нулю:
![]()
или
![]() ;
;
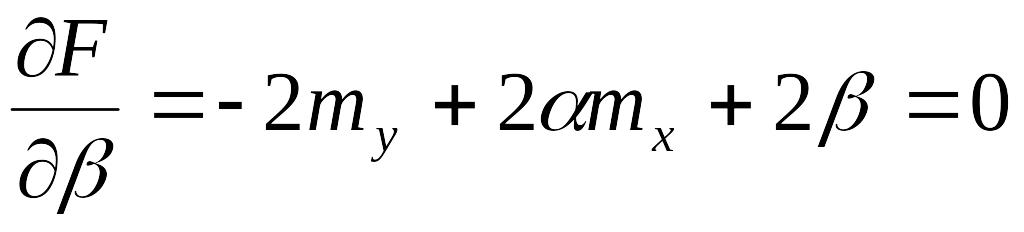 ,
или
,
или
![]() .
.
Таким образом, получаем систему двух уравнений:

Из этой
системы находим параметры
и
.
Для этого умножим второе уравнение
системы на
![]() и сложим с первым. Получим
и сложим с первым. Получим
![]() ,
,
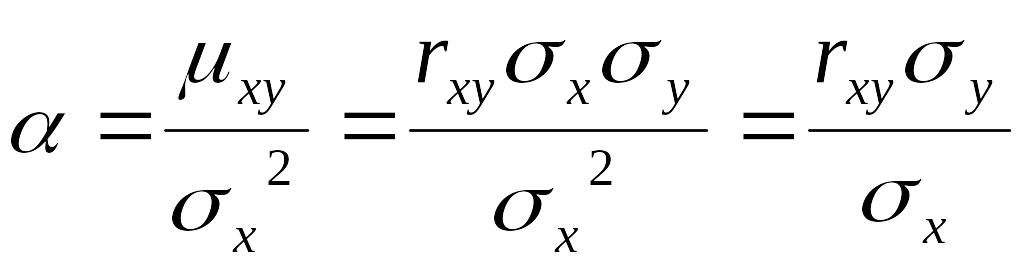 .
Подставив полученное выражение для
во второе уравнение системы, найдем
.
Подставив полученное выражение для
во второе уравнение системы, найдем
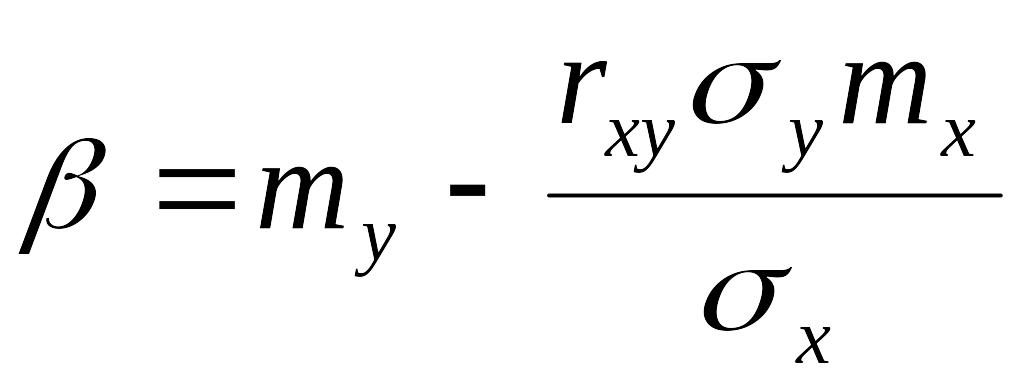 .
.
После подстановки и в выражение функции , получим:
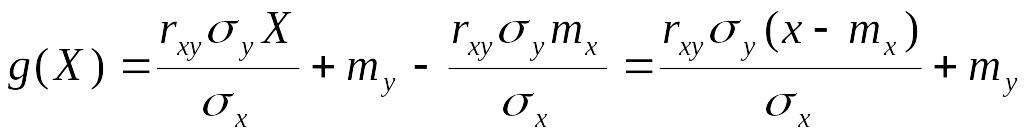 .
.
Условное
математическое ожидание этого выражения
при
![]() запишется в виде
запишется в виде
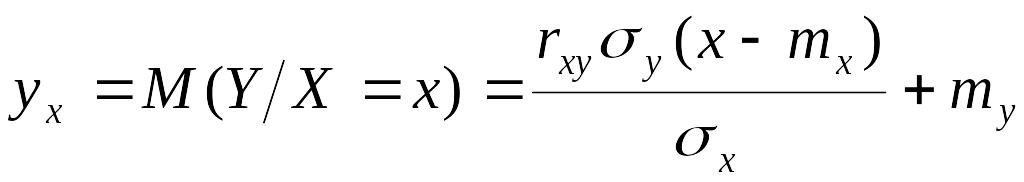 ,
что и требовалось доказать.
,
что и требовалось доказать.
Метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции, называется методом наименьших квадратов.
Распределение 2
Пусть
имеется n независимых случайных
величин 1, 2,
..., n,
распределенных по нормальному закону
с математическим ожиданием, равным
нулю, и дисперсией, равной единице. Тогда
случайная величина
![]() распределена по закону, который называется
«распределение 2»
или «распределение Пирсона».
Очевидно, что она может принимать лишь
неотрицательные значения. Число n
называется числом степеней свободы.
распределена по закону, который называется
«распределение 2»
или «распределение Пирсона».
Очевидно, что она может принимать лишь
неотрицательные значения. Число n
называется числом степеней свободы.
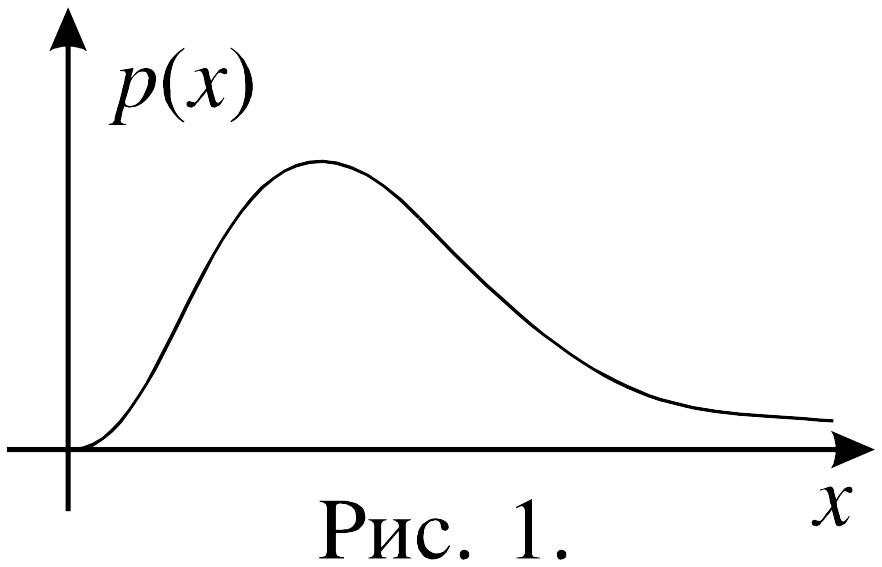
При n>1 график плотности распределения случайной величины 2 представляет собой кривую, изображенную на рисунке 1.
Для того, чтобы определить вероятность попадания случайной величины 2 в какой-либо промежуток из множества положительных чисел, пользуются таблицей распределения 2.
Таблица 1
q n |
0,99 |
0,975 |
0,95 |
... |
0,1 |
0,05 |
0,01 |
1 |
0,0315 |
0,0398 |
0,0239 |
... |
2,71 |
3,84 |
6,63 |
... |
... |
... |
... |
... |
... |
... |
... |
10 |
2,56 |
3,25 |
3,94 |
... |
16,0 |
18,3 |
23,2 |
... |
... |
... |
... |
... |
... |
... |
... |
Обычно такая таблица позволяет по вероятности q и по числу степеней свободы n определить так называемый квантиль q2, если q и q2 связаны соотношением:
P(2 > q2) = q.
Эта формула означает вероятность того, что случайная величина 2 примет значение, большее, чем определенное значение q2, равна q.
Таблица 1 представляет собой фрагмент таблицы распределения 2. Из него видно, что случайная величина 2 с 10-ю степенями свободы с вероятностью q=0,95 принимает значение, большее 3,94, а та же величина с одной степенью свободы с вероятностью q=0,975 превышает 0,00098.
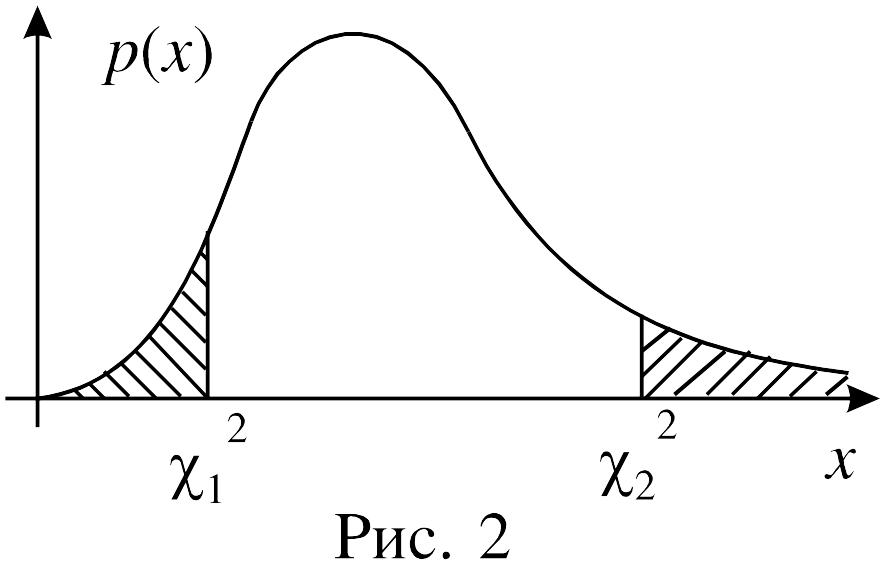
Задача. Найти интервал (12, 22), в который случайная величина 2 с 10-ю степенями свободы попадает с вероятностью, равной 0,9.
Решение. График плотности распределения 2 с 10-ю степенями свободы схематично изображен на рисунке 2. Будем считать, что площади заштрихованных областей (правая область не ограничена справа) равны между собой. Примем условия:
P(2 < 12) = P(2 > 22) = (1 - 0,9)/2 = 0,05, (1)
тогда P(12 < 2 < 22) = 0,9.
Равенства (1) сразу позволяют по таблице определить: 22 = 18,3. Для определения левой границы интересующего нас интервала придется воспользоваться очевидным равенством P(2>12)=0,95. Из таблицы 1. определяем: 12=3,94 , и теперь можно сформулировать ответ задачи: значение случайной величины 2 с вероятностью 0,9 принадлежит интервалу (3,94; 18,3).
