Выборочные уравнения регрессии
Для
определения значений теоретических
коэффициентов, входящих в уравнения
регрессии, вообще говоря, необходимо
знать и использовать все значения
переменных генеральной совокупности,
что практически невозможно. В связи с
этим по выборке ограниченного объема
строится так называемое выборочное
(эмпирическое) уравнение регрессии.
В силу несовпадения статистической
базы для генеральной совокупности
и выборки оценки коэффициентов,
входящих в уравнение регрессии,
практически всегда отличаются от
истинных (теоретических) значений, что
приводит к несовпадению эмпирической
и теоретической линий регрессии.
Различные выборки из одной и той же
генеральной совокупности обычно приводят
к отличающимся друг от друга оценкам.
Задача состоит в том, чтобы по конкретной
выборке
найти оценки неизвестных параметров
так, чтобы построенная линия регрессии
являлась бы наилучшей, среди всех других
линий.
Линейная регрессия
Если функция регрессии линейна, то говорят о линейной регрессии. Линейная регрессия (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Для этого простейшего случая имеем:
или
Последнее
соотношение называется теоретической
линейной регрессионной моделью;
коэффициенты
– теоретическими параметрами регрессии;
– случайным отклонением.
По выборке ограниченного объема строится выборочное уравнение регрессии:
, (1)
где
– оценки неизвестных параметров
,
называемые выборочными (эмпирическими)
коэффициентами регрессии,
– оценка условного математического
ожидания
.
Для величин
справедлива формула:
, (2)
где отклонение
– оценка теоретического отклонения
.
Построенная прямая выборочной регрессии должна наилучшим образом описывать эмпирические данные, т.е. коэффициенты должны быть такими, чтобы случайные отклонения были минимальны. Наиболее распространенным методом нахождения коэффициентов уравнения регрессии является метод наименьших квадратов (МНК).
Если по выборке требуется определить оценки выборочного уравнения регрессии (2), то вводится в рассмотрение и минимизируется функция:
.
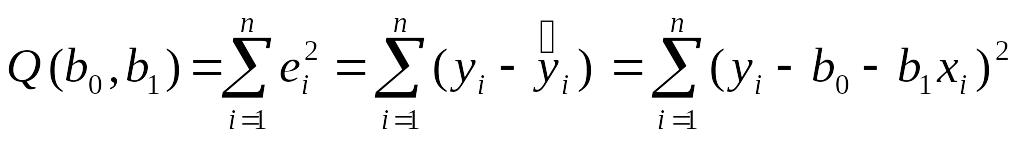Необходимым условием существования минимума данной функции двух переменных является равенство нулю ее частных производных по неизвестным параметрам :
.
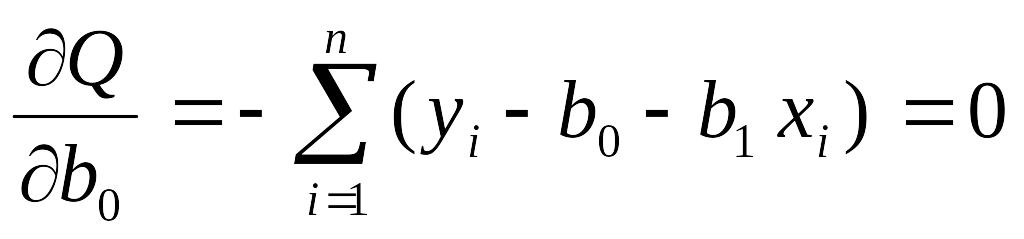
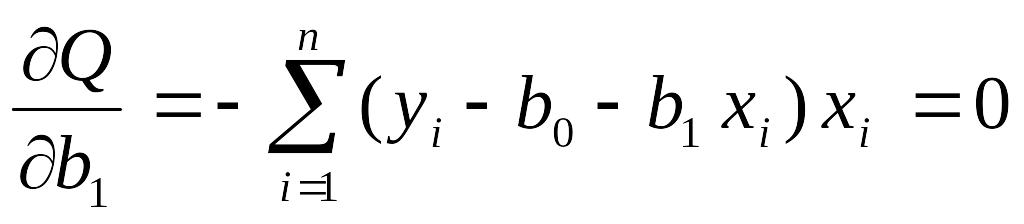Отсюда:
,
выразив из последних соотношений коэффициенты, получим окончательно:
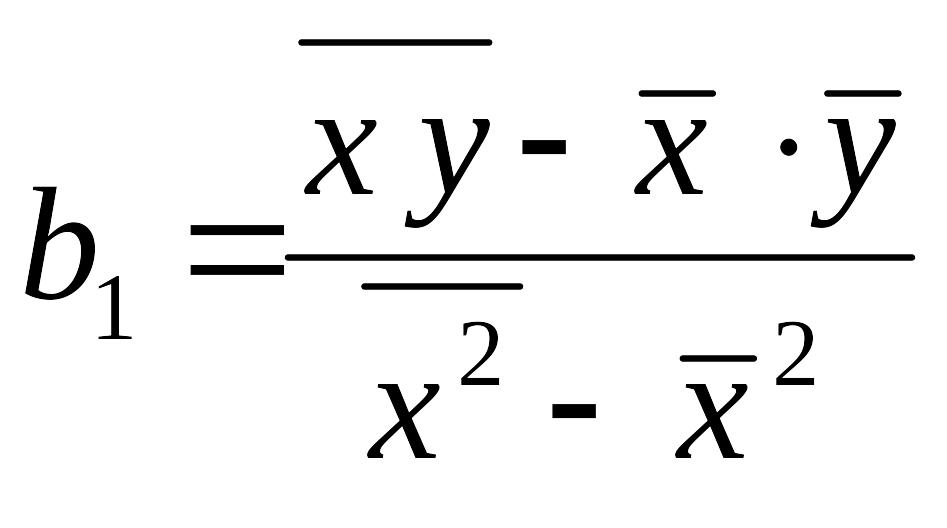
, (3)
где введены обозначения:
.
Множественная линейная регрессия
На любой экономический показатель, чаще всего, оказывает влияние не один, а несколько факторов. Например, спрос на некое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае рассматривается множественная регрессия:
.
Теоретическое линейное уравнение регрессии имеет вид:
,
или для
индивидуальных наблюдений
:
.
Параметры
регрессии могут быть найдены в случае,
если
.
Самым распространенным методом оценки
параметров уравнения множественной
линейной регрессии также является метод
наименьших квадратов.