В) Матричний метод розв’язування систем лінійних рівнянь Поняття оберненої матриці

Матриця А^-1 називається оберненою для квадратної матриці А, якщо АА^-1=А^-1А=Е. Тут Е – одинична матриця.

Виберемо довільну матрицю А п-го порядку:

Утворимо матрицю , елементами якої є алгебраїчні доповнення A_ij до відповідних елементів а_ij матриці, транспонованої до матриці А:

Матрицю називають взаємною (приєднаною) для матриці А. За правилом множення матриць отримаємо:

Матриця називається невиродженою, якщо її визначник не дорівнює нулю, і виродженою, якщо дорівнює нулю.

Відомо, що визначник добутку квадратних матриць дорівнює добутку визначників цих матриць, тому із останнього виразу випливає, що якщо матриця А невироджена, то взаємна їй матриця А^* теж буде невиродженою, причому

Дійсно, звідки при і випливає сформульоване твердження. Тому із АА^-1=Е випливає Це означає, що обернена матриця А^-1 існує тільки для невиродженої матриці А, бо в іншому випадку не буде виконуватись остання рівність.

Для довільної невиродженої матриці А існує тільки одна обернена матриця А^-1.

Дійсно, якби існувала ще одна матриця А₁, обернена до А, тобто така, що

АА₁=А₁А=Е, то

А₁АА^-1=(А₁А)А^-1=ЕА^-1=А^-1,

А₁АА^-1=А₁(АА^-1)=А₁Е=А₁,

звідки А₁=А^-1.

Із випливає тобто

Загальний вигляд оберненої матриці до А:

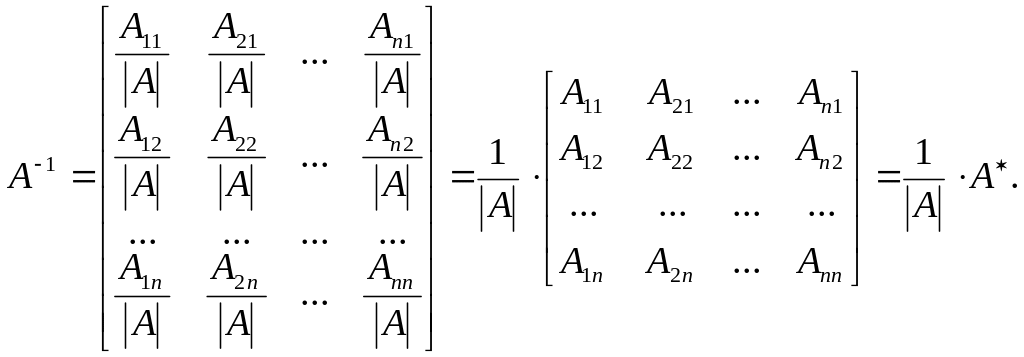
Якщо матриця А невироджена, то кожне з рівнянь АХ=В та УА=В має розв’язки:

Х=А^-1В, У=ВА^-1.

Приклад 1.

Знайти матрицю, обернену до матриці:

Розв’язання.

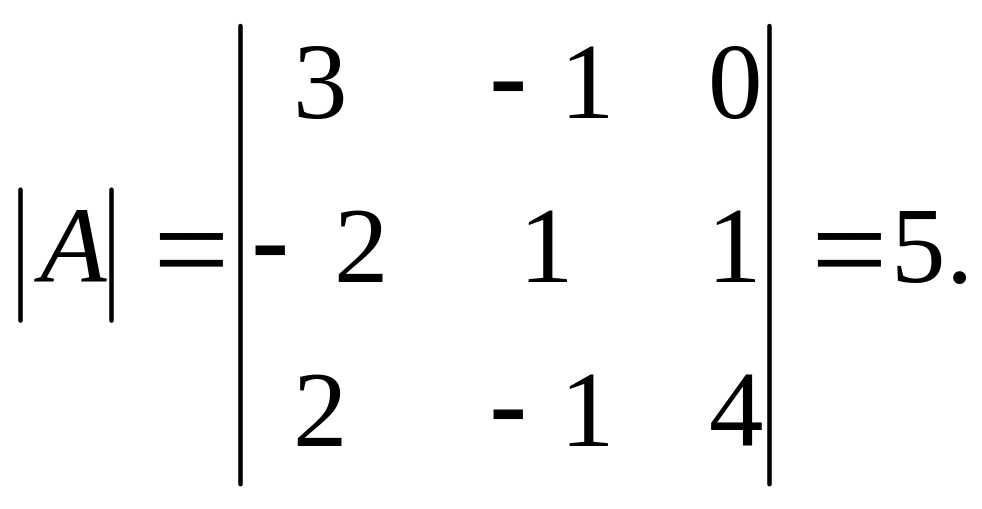Отже, обернена А^-1 існує:

А₁₁=5, А₁₂=10, А₁₃=0,

А₂₁=4, А₂₂=12, А₂₃=1,

А₃₁=-1, А₃₂=-3, А₃₃=1.

Приклад 2.

Розвязати рівняння АХ=В і УА=В, якщо

Розв’язання.

Матриця А^-1 невироджена і рівна Тому

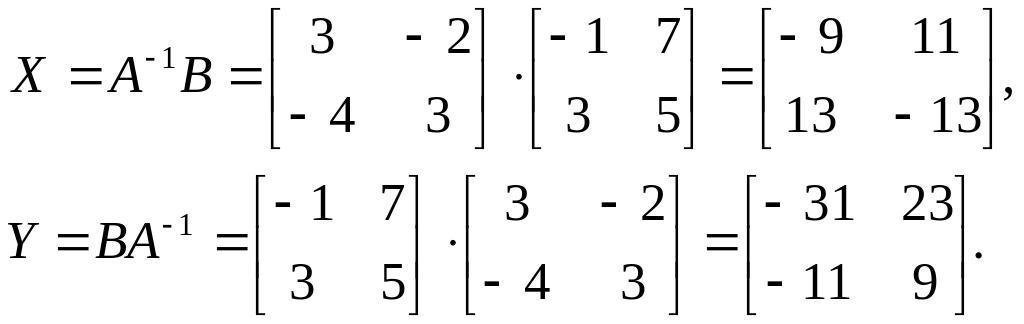
Матрична форма запису системи лінійних рівнянь

Для системи m лінійних рівнянь з п невідомими

вводяться наступні позначення:

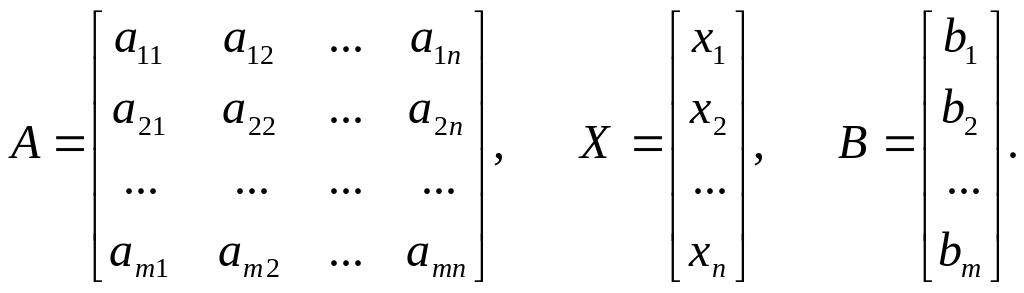
Тоді система лінійних рівнянь запишеться у вигляді матричного рівняння АХ=В. Це рівняння називають матричною формою запису систем лінійних рівнянь. Нехай число рівнянь m у системі дорівнює кількості невідомих п, причому визначник цієї системи відмінний від нуля. Якщо дане матричне рівняння має розв’язок тобто виконується рівність АХ^*=В, то, помноживши зліва обидві частини цієї рівності на А^-1, отримаємо А^-1АХ^*=А^-1В, звідки Х^*=А^-1В, тобто матимемо матричний вигляд розв’язку заданої системи лінійних рівнянь.

Отже, якщо вихідне матричне рівняння із невиродженою матрицею А має розв’язок, то він єдиний і задається формулою

Х^*=А^-1В.

Приклад.

Розв’язати систему лінійних рівнянь матричним способом

Розв’язання.

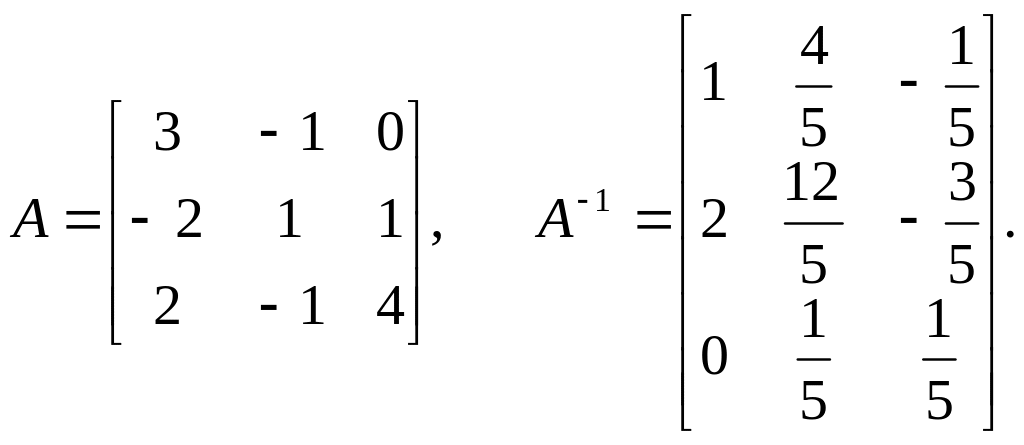
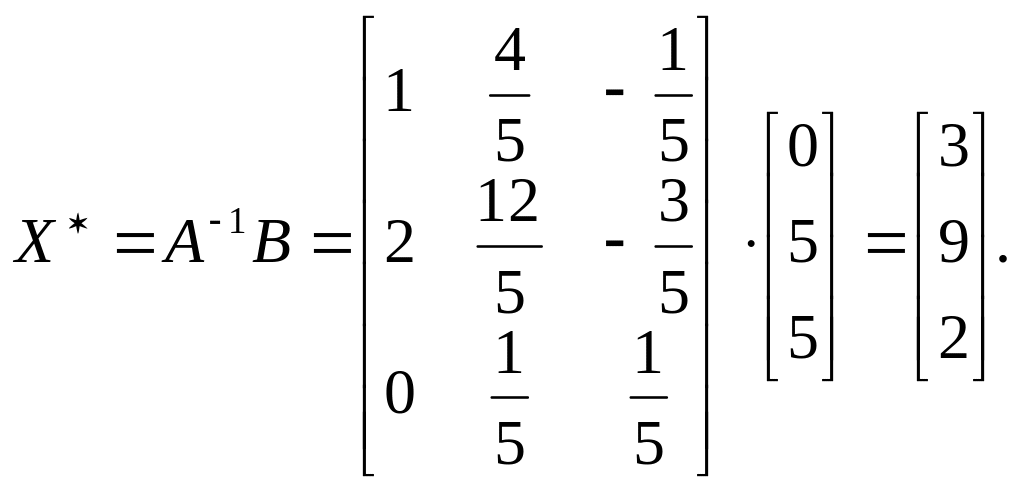
Отже, розв’язок (3;9;2).

12