Лекція 9 Евклідові простори

§1. Основні поняття

А) Скалярний добуток

Введемо у векторному просторі спосіб вимірювання довжин векторів і кутів між ними. Для цього використаємо поняття скалярного добутку.

У звичайному тривимірному просторі скалярним добутком двох векторів називається добуток їх довжин, помножений на косинус кута між ними. Для векторів х та у їх скалярний добуток позначається (х, у). Отже,

(x, y)= (x,y).

Властивості:

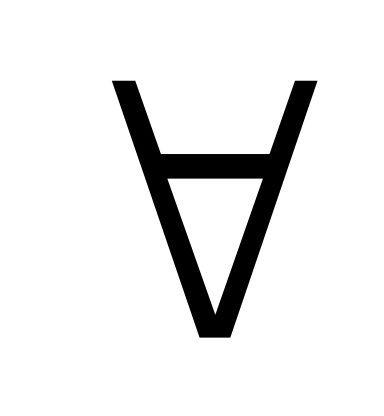1. x, y V [(x, y)=(y, x)]. В комплексному просторі (х, у)=

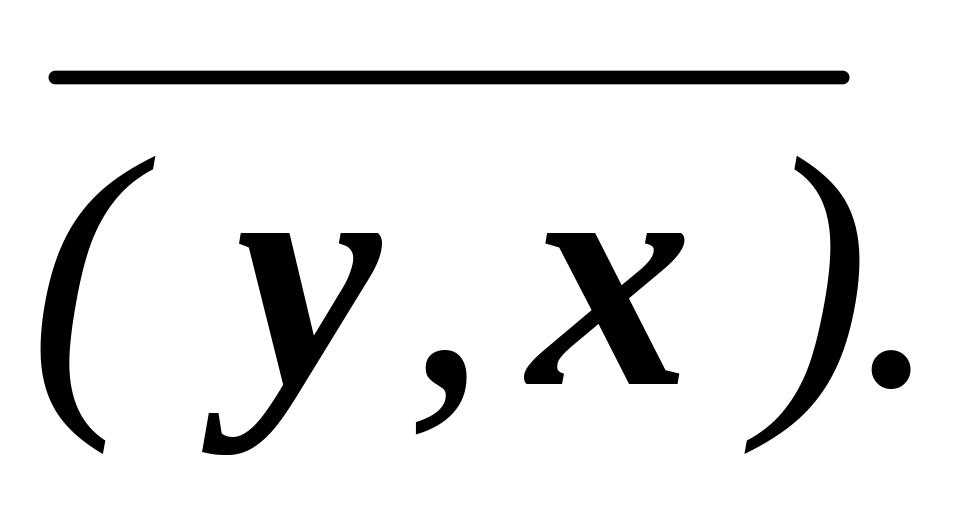
2. x, y V , [(αx, y)=α(x, y)].

3. x, y, z V [(x+y, z)=(x, z)+(y, z)].

4. x V [(x, x) ≥ 0, причому із (х, х)=0 випливає х=0].

У п - вимірному векторному просторі V вважається заданим скалярний добуток, якщо кожній парі векторів x, y V поставлено у відповідність число (х, у) так, що виконуються умови 1-3.

Векторний простір, в якому заданий скалярний добуток, який задовольняє умовам 1 - 4, називається евклідовим простором.

Із рівностей 1-3 випливають співвідношення:

2′. (x, αy)=(αy, x)=α(y, x)=α(x, y) (V - дійсний),

(x, αy)= = = (x, y) (V – комплексний),

3′. (z, x+y)=(x+y, z)=(x, z)+(y, z)=(z, x)+(z, y).

Приклад.

Якщо в п – вимірному векторному просторі вибрано деякий базис e=(e₁,e₂,…,e_n), в якому вектори х та у мають наступні розклади:

x=x₁e₁+x₂e₂+…+x_ne_n, y=y₁e₁+y₂e₂+…+y_ne_n,

то їх скалярний добуток визначається рівністю:

(x,y)=x₁y₁+x₂y₂+…+x_ny_n

(властивості 1-4 перевіряються безпосередньо).

Довжиною вектора х називається корінь квадратний із його скалярного квадрата:

Кут між векторами х та у визначається рівністю

.

Нерівність Коші-Буняковського.

або або |(x, y)| .

Модуль скалярного добутку двох векторів не перевищує добутку їхніх модулів.

Доведення.

Якщо α – довільне дійсне число , то для вектора х-αу (із умови 4) маємо

(х-αу, х-αу) ≥ 0,

звідки (із 1-3) отримаємо:

(х,х)-2α(х,у)+α²(у,у) ≥ 0.

Отримано квадратний тричлен відносно α. Оскільки він має бути невід’ємним при всіх α, то його дискримінант недодатний, тобто

що й треба довести. ▲

Очевидним є те, що рівність досягається (умова 4) тільки при х-αу=0, тобто х = αу (вектори х та у пропорційні).

Нерівність Коші-Буняковського підтверджує правомірність користування формулою для знаходження cos , оскільки

Вектори х та у, скалярний добуток яких дорівнює нулю, називаються ортогональними.

Б) Ортонормований базис

Базис е₁, е₂, ..., е_п евклідового простору називається ортогональним, якщо при .

Якщо, крім того, при і=1, 2, ..., п, то базис називається ортонормованим.

Теорема 1. Ортогональна система векторів лінійно незалежна.

Доведення.

Нехай ненульові вектори х₁, х₂, ..., х_k попарно ортогональні: (х_і,x_j)=0 при Розглянемо рівність

α₁х₁+α₂х₂+...+α_kx_k=0

і доведемо, що всі α_і=0 при і=1, 2, ..., k. Помножимо обидві частини скалярно на х_і, і=1, 2, ..., k. Отримаємо

α₁(х₁,х_і)+α₂(х₂,х_і)+...+ α_k(x_k,x_i)=0,

звідки із врахуванням (x_i,x_j)=0 при та при всіх і=1, 2, ..., k) випливає, що α_і=0 при і=1, 2, ..., k, що й треба довести. ▲

Теорема 2. В кожному евклідовому просторі існують ортонормовані базиси.

Доведення.

Нехай е₁, е₂, ..., е_п – довільний базис простору V. Покладемо

f₁=e₁,

f₂= αf₁+e₂, причому α підберемо так, щоб вектори f₁ і f₂ були ортогональними: (е₂+αf₁,f₁)=(e₂,f₁)+α(f₁,f₁)=0, звідки .

Оскільки , то знаменник Із лінійної незалежності векторів e₁=f₁ та e₂ випливає, що

Припустимо тепер, що попарно ортогональні ненульові вектори

f₁, f₂, …, f_k-1 вже знайдені. Покладемо

f_k=β₁f₁+β₂f₂+…+β_k-1f_k-1+e_k

і підберемо числа β₁, β₂, ..., β_k-1 так, щоб вектор f_k був ортогональним до всіх попередніх f₁, f₂, …, f_k-1. Для цього потрібно, щоб виконувались рівності

(f_k,f_i)=β_i(f_i,f_i)+(e_k,f_i)=0

при і=1, 2, ..., k-1, звідки

.

Знаменник , оскільки всі вектори за припущенням. Оскільки вектори е₁, е₂, ..., е_k лінійно незалежні, то і отриманий вектор f_k теж буде ненульовим.

Такий процес продовжуватимемо доти, поки не знайдемо останнього ненульового вектора

f_n=γ₁f₁+γ₂f₂+…+γ_n-1f_n-1+e_n,

ортогонального до всіх попередніх векторів f₁, f₂, …, f_n-1. Згідно теореми 1 ортогональні вектори f₁, f₂, …, f_n лінійно незалежні і, отже, утворюють ортогональний базис. Якщо кожний із цих векторів поділити на його модуль, то отримаємо ортонормований базис, утворений векторами

▲

Описаний спосіб отримання ортонормованої системи векторів із заданої лінійно незалежної системи називають процесом ортогоналізації.

Якщо V₁ – підпростір V і е₁, е₂, ..., е_k – ортонормований базис V₁, то вектори е₁, е₂, ..., е_k можна включити в ортонормований базис всього простору V. Дійсно, для доведення достатньо доповнити е₁, е₂, ..., е_k до базису простору V і здійснити ортогоналізацію отриманої множини векторів, починаючи із

е₁, е₂, ..., е_k.