Б) Метод Крамера розв’язування систем лінійних рівнянь

Розглянемо систему п лінійних рівнянь з п невідомими, визначник d якої відмінний від нуля. Доведемо, що така система сумісна і визначена, і знайдемо формули для знаходження її єдиного розв’язку.

Припустимо, що наша система сумісна. Нехай – деякий її розв’язок. Тоді виконуються рівності:

Помножимо першу з рівностей на алгебраїчне доповнення А_1j елемента a_1j у визначнику системи, другу – на алгебраїчне доповнення A_2j і т. д., нарешті, останню з рівностей – на A_nj ( j=1, 2,..., n ),потім всі отримані рівності додамо. В результаті дістанемо таку рівність:

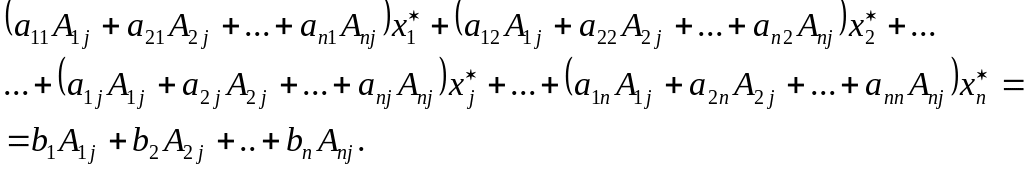
В записаній рівності коефіцієнт біля дорівнює визначнику d матриці системи (теорема 6.1), а всі інші коефіцієнти дорівнюють нулю (теорема 6.2). Вираз у правій частині є розкладом визначника

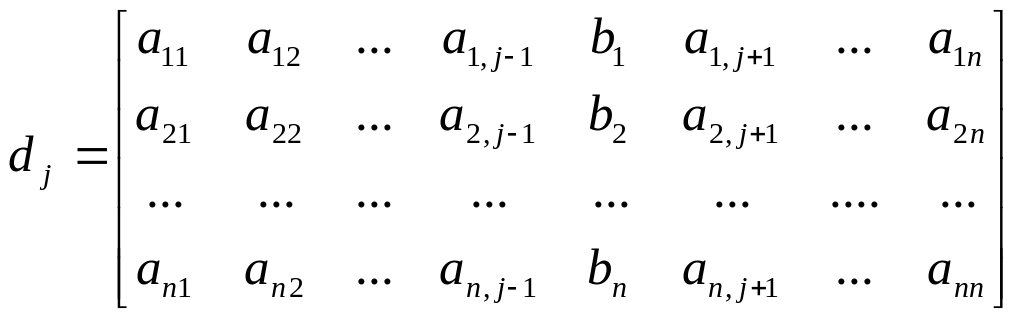
за елементами j-го стовпчика, тобто є визначником d_j, який утворено з визначника d заданої системи рівнянь заміною його j-го стовпчика стовпчиком вільних членів. Тому отримана вище рівність запишеться так:

( j=1, 2,…, n ). Звідси, оскільки d ≠ 0 за умовою, отримаємо

Отже, якщо задана система п лінійних рівнянь з п невідомими сумісна, то вона має єдиний розв’язок

.

Таким чином, задана система або має єдиний розв’язок , або зовсім не має розв’язків. Тому для з’ясування питання про сумісність даної системи досить тільки з’ясувати, чи задовольняє система чисел задану систему рівнянь. Для перевірки підставимо числа в ліву частину і-го рівнянння (і=1, 2,…, п).

(оскільки ).

Отже, множина чисел є розв’язком кожного і-го рівняння (і=1,2,…,п) системи, а, значить, і самої системи.

Таким чином, доведено теорему:

Якщо визначник d системи n лінійних рівнянь з n невідомими відмінний від нуля, то система має єдиний розв’язок: , де – визначник, отриманий із визначника d заміною його j-го стовпчика стовпчиком вільних членів системи.

Отримані формули розв’язку називають формулами Крамера, а саму теорему – правилом Крамера.

Наслідок. Система n лінійних однорідних рівнянь з п невідомими тоді і тільки тоді має розв’язки, відмінні від нульового, коли визначник цієї системи дорівнює нулю.

Дійсно, якби визначник однорідної системи лінійних рівнянь був відмінним від нуля, то ця система мала б єдиний нульовий розвязок, що суперечить умові.

Навпаки, якщо визначник системи дорівнює нулю, то ступінчаста матриця цієї системи п рівнянь з п невідомими має хоча б один нульовий рядок, а, значить, кількість рівнянь у відповідній ступінчастій системі менша за число невідомих, звідки випливає існування вільних невідомих і, отже, нескінченної кількості розв’язків, в тому числі і відмінних від нульового.

Правило Крамера пов’язане з громіздкими обчисленнями, але в тих випадках, коли воно застосовне, є можливість виразити всі компоненти розв’язку системи рівнянь через її коефіцієнти і вільні члени.

Приклад.

Розв’язати систему рівнянь

Розв’язання.

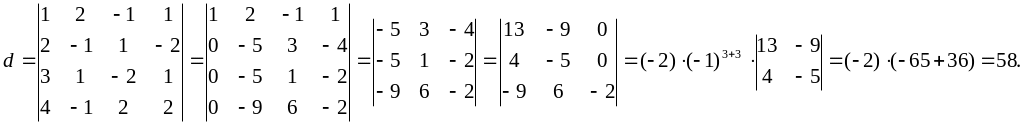
Оскільки d  0, то застосуємо правило Крамера:

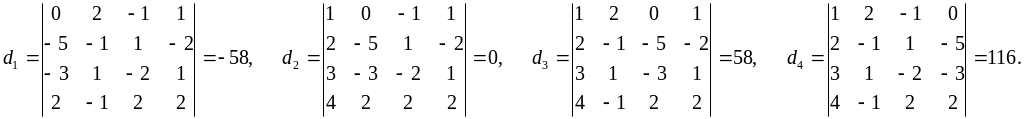
Отже,

Розв’язок: (-1;0;1;2).