19.4. Асимптоти гіперболи

Означення 6. Пряма називається асимптотою кривої ( , якщо віддаль від точки кривої до точки прямої прямує до нуля при необмеженому віддалені точки від початку координат вздовж кривої ( ) в тому чи іншому напрямі (мал.60).

П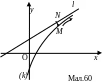 окажемо, що пряма (2.141) є асимптотою гіперболи (2.135). Для цього розглянемо пряму MN, яка паралельна осі Oy (мал.59). Абсциса точки M і точки N одна і та ж, тобто x, а ордината точки M є y, а точки NY.

Знайдемо різницю між ординатами (Y-y) -точок N і M, які мають одну і ту ж абсцису

.

Тепер помножимо і розділимо праву частину цієї рівності на і після спрощень одержимо . Звідси видно, що при необмеженому збільшенні абсциси x різниця Y-y необмежено зменшується . Таким чином, точка гіперболи необмежено віддаляючись по вітці гіперболи, необмежено наближається до асимптоти , але ніколи її не досягає. Значить, гіпербола (2.135) має дві асимптоти і , які співпадають з діагоналями прямокутника і проходять через початок координат.

Приклад 4. Скласти рівняння гіперболи, якщо відомо, що вона проходить через точку M₁(10;5) і має асимптоти та .

Розв’язування. З умови задачі одержуємо, що та координати точки M₁ задовольняють рівнянню гіперболи, тобто Таким чином, одержали систему двох рівнянь з двома

невідомими:

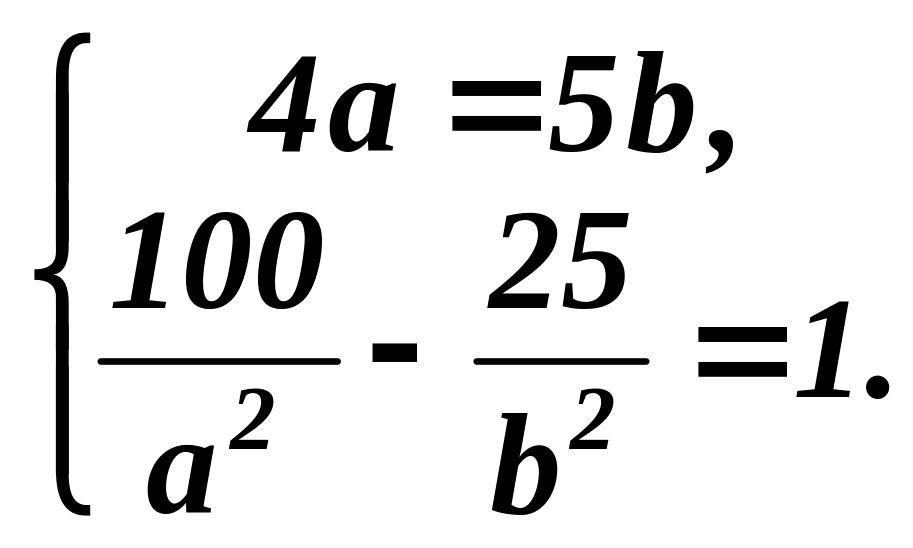
З першого рівняння знаходимо і підставляємо в друге рівняння або

Звідси . Далі знаходимо

Отже, шукане рівняння гіперболи буде

19.5. Парабола та її рівняння

Означення 7. Параболою називається множина точок площини, однаково віддалених від заданої точки, що називається фокусом і від заданої прямої, що називається директрисою.

В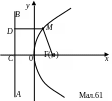 иходячи з означення 7, виведемо рівняння параболи. Нехай пряма AB є директрисою параболи, а точка F є її фокусом (мал.61). Проведемо через точку пряму перпендикулярну до директриси AB і візьмемо цю пряму за вісь абсцис, а за вісь ординат вієьмемо пряму перпендикулярну до вісі абсцис і яка проходить через точку O, середину відрізка CF. Довжину відрізка CF позначимо через p (p>0). Координати фокуса будуть , а рівняння директриси AB є Нехай точка M(x,y) є довільною точкою параболи. Опустимо із точки M перпендикуляр на директрису AB в точці D і сполучимо точку M з фокусом F. Тоді за означенням 7 маємо, що DM=MF Точка D має координати За формулою віддалі між двома точками знаходимо .

Це і буде рівняння параболи відносно вибраної системи координат. Підносячи обидві частини даного рівняння до квадрату, і спростивши, одержимо

. (2.142)

Рівняння (2.142) і є канонічним рівнянням параболи. Як видно з рівняння (2.142) парабола є лінія другого порядку і всі її точки розташовані праворуч від осі . Парабола проходить через початок координат. Розв’язавши рівняння (2.142) відносно одержимо

. (2.143)

Так як , то буде дійсною величиною тільки тоді, коли додатні, а коли то парабола визначена для .

Із (2.143) видно, що кожному значенню відповідає два значення , які рівні за абсолютною величиною, але протилежні за знаком.

Значить вісь є віссю симетрії для параболи.

Точку називають вершиною параболи.

Я кщо x необмежено зростає, то і y необмежено зростає. Величина р називається параметром параболи і при збільшенні р парабола розширюється, тобто її точки будуть віддалятися від осі Ох.

Якщо рівняння параболи має вигляд y²=−2px то вершина параболи знаходиться в початку координат, вісь симетрії є вісь абсцис, але парабола розміщена зліва від осі Oy (мал.62), а директриса такої параболи буде розміщена праворуч від осі ординат, а фокус буде ліворуч від початку координат.

Якщо директриса параболи паралельна вісі абсцис , а фокус знаходиться на вісі ординат, то рівняння параболи має вигляд

x²2py. (2.144)

Парабола (2.144) зображена на мал.63. Це парабола

симетрична відносно осі Oy і розміщена над віссю абсцис, якщо в

р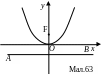 івнянні взяти знак (+) і під віссю абсцис, якщо взяти знак (-).

Якщо в рівнянні (2.144) позначити , то одержимо рівняння параболи , яку вивчають в середній школі.

Приклад 5. Ферми, які підтримують залізнодорожний міст довжиною 112 м, мають вигляд параболи, яка задається рівнянням Знайти рівняння відповідної параболи, якщо найбільша висота мостової арки складає 44м.

Розв’язування. Візьмемо за початок координат вершину ферми. Тоді симетричні точки в основі ферми будуть мати координати (-56,-44) і (56,-44). Підставляючи будь-яку пару координат в рівнян-

ня , одержимо . Звідси .

Таким чином, мостова ферма має вигляд параболи .