Розділ 2. АНАЛІТИЧНА ГЕОМЕТРІЯ І ЕЛЕМЕНТИ

ВЕКТОРНОЇ АЛГЕБРИ

Аналітична геометрія є розділ математики, яка вивчає властивості геометричних фігур алгебраїчними методами. Уже в середній школі до геометрії застосовують алгебру при розв’язуванні багатьох питань. Ще в ст. французький математик Рене Декарт розробив метод координат, який є апаратом аналітичної геометрії. Цей метод дає можливість визначити положення точки на прямій, на площині, на поверхні, а форму ліній і поверхонь задати за допомогою рівнянь, які пов’язують координати їх точок.

§1. Метод координат на прямій та його застосування

Р озглянемо горизонтальну пряму лінію на площині (мал.1). На цій прямій l візьмемо нерухому точку O, що називається початком відліку. Ця точка розбила пряму на два взаємно протилежні напрямки: додатній – вправо і від’ємний – вліво. Взявши деяку одиницю масштабу, вправо від точки Oвідкладаємо додатні числа, а вліво – від’ємні числа. Ці числа відповідають деяким точкам на прямій l і навпаки, отже між точками прямої l та дійсними числами існує взаємно однозначна відповідність. Таку пряму l будемо називати числовою віссю Ox. Точці O, що вважається початком відліку , відповідає число нуль.

Таким чином, ми побудували систему координат на прямій. Візьмемо деяку точку А на числовій осі. Цій точці відповідає деяке число х, яке називається координатою точки А. Це записується А(х).

Будемо вважати відрізок , що відкладений праворуч від точки за додатній, а відрізок відкладений ліворуч від точки О- за від’ємний (мал.1).

Відрізок, у якого початок, а кінець, позначають і називають напрямленим відрізком. Величину відрізка будемо

позначати символом АВ.

Означення. Відрізки, які характеризуються не тільки своєю довжиною, але й напрямом називаються напрямленими

відрізками.

Величина напрямленого відрізка є його довжина, взята з певним знаком.

В ізьмемо на осі -ів дві точки і відповідно з координатами і , тоді і відрізкам і будуть відповідати числа і (мал.2).

Покажемо, що при будь-якому розташуванні точок і

відносно точки величина відрізка буде дорівнювати тобто

(2.1)

Дійсно, нехай точки і розташовані так як на мал.2. Тоді

Коли точки і розташовані так, як на мал.3,

т о але і

Одержимо

Нехай і розташовані по різні сторони відносно точки (мал.4).

Значить .

Якщо а , то величина відрізка буде

Довжина відрізка позначається через і дорівнює

(2.2)

Висновок. Якщо на прямій в деякій системі координат задано дві точки і ,тоді величина відрізка знаходиться із рівності (2.1), а віддаль (довжина) між цими точками за формулою (2.2).

Приклад 1. Задано точки .

Знайти величину відрізків , .

Розв’язування. За формулою (2.1) одержуємо: .

Приклад 2. Знайти віддаль між точками

Розв’язування. За формулою (2.2) одержимо

§2. Прямокутна система координат на площині

та її застосування

Положення точки на прямій, як ми бачили, визначається одним числом – її координатою, а положення точки на площині, як ми побачимо, визначається упорядкованою парою чисел (тобто вказано яке із чисел є першим, а яке другим).

В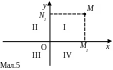 ізьмемо на площині дві взаємно перпендикулярні осі і назвемо їх осями координат (мал.5).

Точка перетину осей координат O називається початком координат. Осі координат ( - вісь абсцис, горизонтальна, вісь ординат, вертикальна ). Осі координат і ділять площину на чотири частини, які називаються квадрантами ( або координатними кутами). Частина площини, що міститься між додатними осями і називається першим квадрантом. Нумерація квадрантів іде проти годинникової стрілки.

Нехай точка - довільна точка площини. Опустимо з цієї точки перпендикуляри на вісь і , основи цих перпендикулярів позначимо відповідно через і , тобто і є проекціями точки на координатні осі. Позначимо координату точки на осі через а координату точки на осі через Числа назвемо координатами точки на площині ( абсциса, - ордината) . Це позначимо .

Таким чином, система координат на площині встановлює взаємно однозначну відповідність між множиною всіх точок

площини і множиною всіх упорядкованих пар дійсних чисел.

• Найпростіші задачі на застосування методу координат.

а) Віддаль між двома точками на площині.

Нехай задані дві точки з своїми координатами: , . Треба знайти віддаль між цими точками. Зробимо малюнок (мал.6).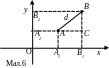

Точки і спроектуємо на координатні осі. Їх проекції на вісь позначимо відповідно через і , а на вісь - відповідно через і .

Тоді

Через точку проведемо пряму, паралельну осі абсцис до перетину з прямою в точці . З одержаного прямокутного трикутника за теоремою Піфагора знаходимо

На основі формули (2.2) дану рівність перепишемо так:

, або (2.3)

Знак перед коренем у формулі (2.3) береться (+) тому, що віддаль – величина додатна.

Зауваження. Різниця координат у формулі (2.3) підноситься до квадрату і тому немає значення, яку точку вважати першою, а яку другою.

Приклад . Знайти віддаль між точками i .

Розв’язування. За формулою (2.3) знаходимо

б) Поділ відрізка в заданому відношенні.

Нехай на площині задано дві довільні точки A(x₁,y₁) і B(x₂,y₂) Вважаємо A(x₁,y₁) першою точкою, а B(x₂,y₂) другою точкою. Проведемо через ці точки пряму(мал.7).

Нехай точка лежить на відрізку і ділить його на два відрізки і , причому відношення їх дорівнює , тобто (число відоме). Випадок, коли точка співпадає з точкою виключаємо, бо знаменник перетворюється в нуль. Наша задача полягає в тому, щоб знайти координати точки через координати точок , та число .

Спроектуємо точки та на координатну вісь (мал.7) і позначимо їх проекції через , та . Використовуючи теорему про пропорційні відрізки, що містяться між паралельними прямими, одержимо Відомо, що тоді Розв’язуючи цю рівність відносно знаходимо

Аналогічно, спроектувавши точки та на координатну вісь (мал.7) і зробивши необхідні викладки, як вище, знаходимо ординату точки :

Отже, координати точки , яка ділить відрізок

у відношенні (рахуючи від до ), обчислюються за формулами

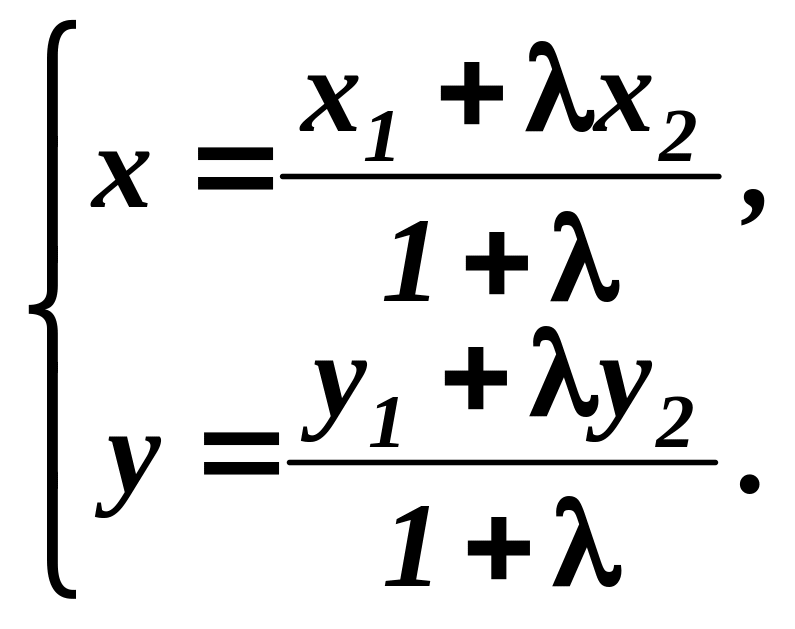(2.4)

Якщо точка є серединою відрізка , то і тоді

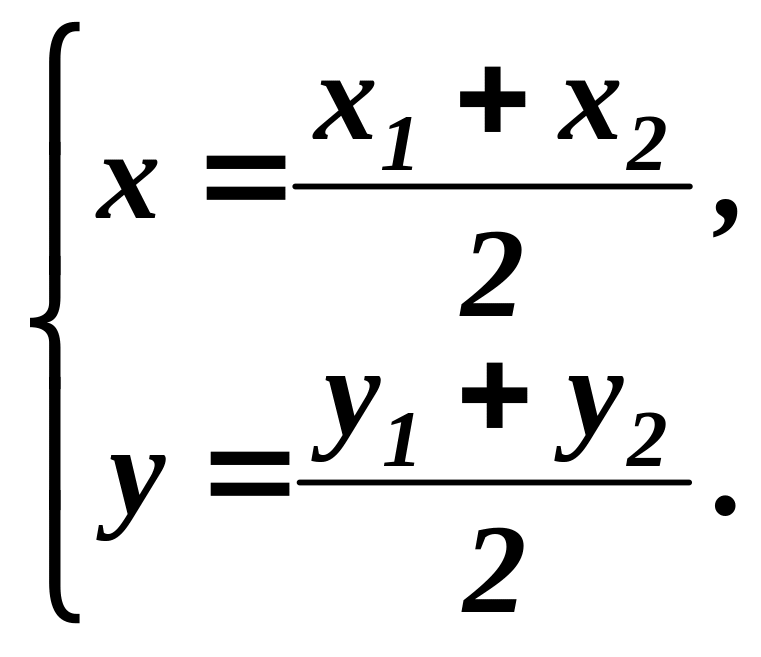(2.5)

Зауваження. При одержанні формул (2.4) ми допускали, що відрізок не паралельний ні одній з осей координат. Однак одержані формули (2.4) справедливі і тоді , коли відрізок паралельний вісі ( ), або осі ( .

Крім цього, все викладене вище справедливе й тоді, коли точка знаходиться зовні , тобто на його продовженні.

Приклад 1. Дано дві точки A(7;-2)і B(-3;-5). На продовженні прямої знайти точку C(x,y), віддаль від якої до точки A в п’ять раз більша за віддаль до точки B. Знайти довжину

Р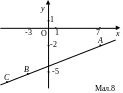 озв’язування. Зробимо малюнок.

За умовою задачі (мал.8) Тепер за формулою (2.4) знаходимо

Значить, точка .

Довжину знаходимо за формулою (2.3)

.

Приклад 2. Знаючи координати вершин трикутника , і , знайти точку перетину медіан трикутника.

Розв’язування. Координати точки (середина сторони ) буде , ,тобто .

Шукана точка ділить кожну медіану у відношенні , рахуючи від вершини. Тепер підставляючи у формули (2.4) та координати точок і , знайдемо координати шуканої точки .

Отже,