19.3. Гіпербола та її рівняння

Означення 4. Гіперболою називається множина точок площини, абсолютне значення різниці віддалей яких від двох заданих точок, які називаються фокусами, є величина стала.

Ґ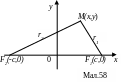 рунтуючись на означенні 4 виведемо канонічне рівняння гіперболи. Нехай задані дві точки і є фокусами гіперболи, позначимо віддаль між ними через а абсолютну величину різниці віддалей точки гіперболи від точок і позначимо через За вісь абсцис візьмемо пряму, яка проходить через фокуси, а за вісь ординат візьмемо пряму перпендикулярну до вісі абсцис, яка проходить через середину відрізка (мал.58), тобто через точку Тому що , то координати фокусів будуть відповідно і , а фокальні радіуси відповідно де довільна точка гіперболи.

Користуючись формулою віддалл1 між двома точками і означенням 4, маємо рівняння гіперболи

. (2.130)

Запишемо це рівняння в такому вигляді

або

. (2.131)

Підносячи до квадрату обидві частини цього рівняння, одержимо,

або після спрощення . Знову підносячи обидві частини одержаного рівняння до квадрату, одержимо після спрощень

. (2.132)

Розділивши обидві частини рівняння (2.132) на одержимо

. (2.133)

Покажемо, що Тому що в будь-якому трикутнику різниця двох сторін менша третьої, то або або .Тоді величина додатна і її позначимо через . Тобто

. (2.134)

Підставляючи (2.134) в (2.133), одержимо канонічне рівняння гіперболи

. (2.135)

Рівняння (2.135) є рівняння другого степеня, значить гіпербола є крива другого порядку. Дослідимо форму гіперболи за її рівнянням (2.135). Оскільки рівняння містить і тільки в парних степенях, то гіпербола симетрична відносно обох осей координат.

Знайшовши та із рівняння (2.135), одержимо

, (2.136)

. (2.137)

Із рівняння (2.136) можна зробити такі висновки:

а) значення у уявні, якщо х<a значить гіпербола не перетинає вісі Оу і не має точок, що знаходяться в полосі, обмеженій прямими х a.

б) коли значить гіпербола перетинає вісь абсцис у двох точках і , які називаються вершинами гіперболи.

в) для кожного ордината має два значення, які відрізняються тільки знаком, звідси випливає, що гіпербола симетрична відносно осі

Рівняння (2.137) показує, що гіпербола симетрична і відносно вісі

П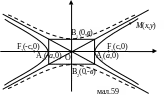 ри необмеженому зростанні абсциси ордината також необмежено зростає. Так як гіпербола знаходиться поза полосою, обмеженою прямими , то гіпербола складається Із двох окремих віток (мал.59).

Відрізок називається дійсною віссю гіперболи, а точки і вершинами гіперболи. Відрізок , що з’єднує точки і називається уявною віссю гіперболи. Точки і називаються фокусами гіперболи.

Гіпербола, яка визначається рівнянням має дійсну вісь а уявну вісь (показано на мал.59 пунктиром) називається спряженою по відношенню до гіперболи .

Якщо дійсна і уявна осі рівні, то гіпербола називається рівносторонньою, а її рівняння буде

Степінь стискування гіперболи характеризується її ексцентриситетом.

Означення 5. Ексцентриситетом гіперболи називається відношення віддалі між фокусами до довжини її дійсної вісі , тобто

. (2.138)

Так як для гіперболи то

Примітка. Для гіперболи легко показати як пов’язані і з а саме ,

; (2.139)

,

. (2.140)

Формули (2.139) і (2.140) одержуються аналогічно як і для еліпса.

Представляємо читачеві самостійно переконатися в справедливості формул (2.139) і (2.140).