1.8.5. Моделирование случайных величин с усеченным нормальным распределением

Усеченное нормальное распределение случайной величины х задается четырьмя параметрами: математическим ожиданием М(Х), средним квадратическим отклонением с(Х), а также мини­мальным и максимальным значениями и х₂ (точками усечения).

Функция распределения случайной величины х определяется равенством

О при х < jc,;

F(x) = 1

А =

[ФоС ) - Ф0С1)] ■^А при х, < х < х₂;

1 при X > х₂,

^ГДе ^ ⁼ Фс(/₂)-Фо('.)^;

х-М(Х)_ х, - М(Х) _ х₂ -М(Х) ' ~ ст(А-) ' ''~ o(Z) ' ^h ~ ст(А-)

Существуют также формулы для расчета математического ожи­дания, дисперсии и среднего квадратического отклонения слу­чайной величины х. Однако с достаточной для практики точно­стью при моделировании случайной величины с усеченным нормальным распределением можно обойтись без расчетов по формулам.

Для определения возможных значений случайной величины с этим распределением можно использовать алгоритм, схема кото­рого приведена на рис. 1.5.

Рис. 1.5. Схема алгоритма моделирования случайной величины с усеченным нормальным распределением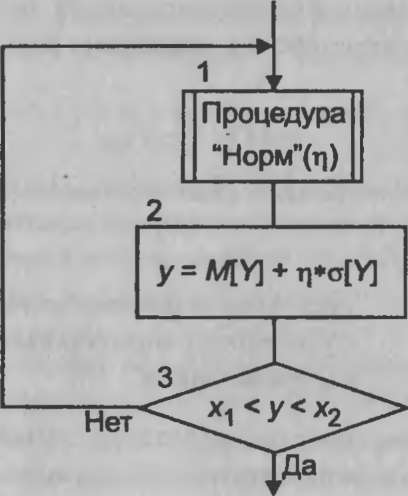

Оператор 1 обращается к процедуре моделирования возможных значений нормированной и центрированной случайной величины г| с нормальным распределением. Оператор 2 вычисляет значение случайной величины у с заданными параметрами M(Y) и ст(У).

Условный оператор 3 проверяет условие попадания случай­ной величины у в неусеченную область. При выполнении этого условия значение случайной величины у с усеченным нормаль­ным распределением считается найденным. В противном случае управление в алгоритме передается вновь на вход оператора 1 и генерируется другая случайная величина.

1.8.6. Моделирование случайных величин с произвольным распределением

Пусть случайная величина х задана в интервале (а₀, aj кусоч­но-постоянной функцией f(x). Это значит, что интервал разбит на п частичных интервалов и плотность распределения f(x) на каждом из них постоянна (рис. 1.6).

-т			Рз
		р2		1 1
					Рп	►

О ^ао ^а1 ^а2 ^а3 ^ал-1

Рис. 1.6. Плотность распределения произвольной функции

Целесообразно выбрать величины а_А так, чтобы вероятности попадания в любой частичный интервал Р* были одинаковы, т. е.

|f(x)dx=I {к =1,2 ri).

^я 1.-1

Из условия постоянства функции на каждом частичном ин­тервале следует, что случайная величина х может быть определе­на по формуле

х= а*_ч + z(а* - а*_,) (к = 1, 2,...,«), (1.4)

где z - возможное значение (реализация) случайной величины, равномерно распределенной в интервале (0,1); а* , - левая граница частичного интервала;

&_к - правая граница частичного интервала.

Попадание в любой частичный интервал можно рассматри­вать как событие, входящее в полную группу несовместных со­бытий. Поэтому процедура моделирования в общем случае со­стоит в следующем.

1. С помощью датчика случайных чисел с равномерным рас­пределением, вырабатывающего величину z, моделируют диск­ретную случайную величину - номер интервала к.

2. Вторично разыгрывают случайную величину z и опреде­ляют возможное значение случайной величины х по формуле (1.4).

Схема алгоритма показана на рис. 1.7.

	ДСЧ (z)
6
X = afc-1 +(ak'ak-l)*z

Выход

1.9. СПОСОБЫ ПОСТРОЕНИЯ МОДЕЛИРУЮЩИХ АЛГОРИТМОВ

Существуют следующие способы (или принципы) построения моделирующих алгоритмов:

способ повременного моделирования с постоянным шагом; способ повременного моделирования с переменным шагом; способ последовательной проводки заявок; способ поэтапной последовательной проводки заявок.