Степеневі ряди

Степеневим називається функціональний ряд, який має вигляд

, (14.27)

або в більш загальному вигляді

. (14.28)

Числа називають коефіцієнтами ряду.

Ряд (14.27) завжди збігається при , а ряд (28) при .

Ряд (14.28) легко звести до ряду (14.27) заміною

. (14.29)

Теорема Абеля. 1. Якщо ряд (14.27) збігається при деякому , то він абсолютно збігається при всіх , для яких .

3. Якщо ряд (14.27) є розбіжним при деякому 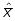, то він є розбіжним при всіх , для яких .

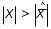14.7.Інтервал збіжності

Область збіжності степеневого ряду (14.27) – це коло з центром на початку координат. Область збіжності степеневого ряду (14.28) – це коло з центром у точці .

Якщо , то коло вироджується в інтервал на осі ОХ. Цей інтервал симетричний відносно початку координат для ряду (14.27) або відносно точки для ряду (14.28).

Число називається радіусом збіжності степеневого ряду. Радіус може змінюватись від 0 до . Для обчислення радіусу збіжності застосовуються формули

; (14.30)

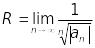. (14.31)

Коли обчислено радіус, треба покласти і дослідити отримані числові ряди на збіжність, бо самі точки можуть і не входити в область збіжності.

14.8.Властивості степеневих рядів

1. Степеневий ряд (14.27) рівномірно збігається на будь-якому проміжку , який розміщений всередині інтервалу збіжності. Тому:

1.1. на проміжку сума степеневого ряду є неперервна функція;

1.2. якщо границі інтегрування і розташовані в середині інтервалу збіжності степеневого ряду, то його можна інтегрувати почленно.

2. Якщо степеневий ряд (14.27) має інтервал збіжності , то ряд, отриманий почленним диференціюванням ряду (14.27), тобто ряд

, (14.32)

має той самий інтервал збіжності і в кожній точці інтервалу похідна від суми степеневого ряду (14.27) дорівнює сумі ряду (14.32).

Приклад 13. Знайти область збіжності степеневого ряду

.

Знайдемо радіус збіжності ряду

.

Маємо

.

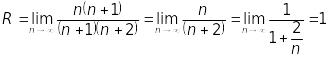При дістанемо числовий ряд

.

Загальний член ряду прямує до нескінченності при :

.

Ряд розбігається.

Нехай . Отримуємо числовий ряд

.

Необхідна умова збіжності не виконується. Тому ряд збігається тільки всередині інтервалу .

Приклад 14. Знайти область збіжності степеневого ряду

.

Знайдемо радіус збіжності ряду, як і в попередньому прикладі:

.

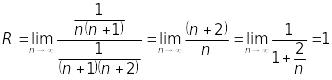При отримаємо знакозмінний числовий ряд

.

Його члени монотонно спадають за абсолютною величиною, і . За ознакою Лейбніца ряд збігається. Ряд з модулів

можна порівняти із збіжним рядом :

.

За теоремою порівняння І ряд з модулів збігається, тобто при маємо абсолютно збіжний ряд.

При отримаємо ряд з додатними членами:

Цей ряд, який вже розглядався, є збіжним.

Заданий ряд збігається як всередині, так і на кінцях інтервалу .

Приклад 15. Знайти область збіжності степеневого ряду

.

Знайдемо радіус збіжності ряду

.

Отримаємо

,

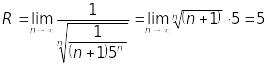тому що

. (14.33)

У заданому ряді центром інтервалу збіжності є точка , тому ряд збігається у внутрішніх точках інтервалу .

Дослідимо ряд на збіжність на кінцях цього інтервалу. При

.

Числовий ряд розбігається, як і гармонійний ряд. При

.

Знакозмінний ряд збігається умовно. Дійсно, ряд з модулів отримано при , він розбігається. Члени ряду монотонно спадні за модулем і

.

Тому за ознакою Лейбніца ряд збігається умовно.

Область збіжності степеневого ряду: .