
- •Лекція 3: загальна теорія систем лінійних алгебраїчних рівнянь
- •2.1. Поняття системи лінійних рівнянь (слр) та її геометрична інтерпретація
- •2.2.Геометрична інтерпретація слр двох рівнянь з двома невідомими
- •2.3. Метод Крамера
- •2.4. Розв'язок системи лінійних рівнянь за допомогою метода послідовного виключення змінних. (Метод Гаусса)
- •Метод Гауса послідовного виключення змінних
- •2.5.Метод Жордана-Гауса повного виключення змінних
Лекція 3: загальна теорія систем лінійних алгебраїчних рівнянь
2.1. Поняття системи лінійних рівнянь (слр) та її геометрична інтерпретація
Система m лінійних рівнянь з n невідомими записується у вигляді:
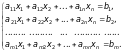 (2.1)
(2.1)
де
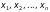 – невідомі системи,
– невідомі системи,
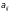 – коефіцієнт при невідомій xj
в і-му
рівнянні, bі
– вільний коефіцієнт в і-му
рівнянні.
– коефіцієнт при невідомій xj
в і-му
рівнянні, bі
– вільний коефіцієнт в і-му
рівнянні.
Матрицею СЛР (1) називається матриця коефіцієнтів при невідомих, тобто

Вектором
невідомих
називається вектор
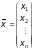 ,
вектором
вільних
членів
називається вектор
,
вектором
вільних
членів
називається вектор
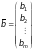 .
.
Розширеною матрицею СЛР (2.1) називається матриця

Очевидно, між системами лінійних рівнянь та їх розширеними матрицями існує взаємно однозначна відповідність (тобто по системі однозначно виписується розширена матриця, та по розширеній матриці однозначно виписується система).
За допомогою введених понять СЛР (2.1) можна подати у наступному матричному вигляді:
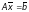 (2.2)
(2.2)
Тут
ліва частина є матричним добутком
матриці А
розмірності
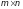 та матриці-стовпчика
та матриці-стовпчика
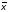 розмірності
розмірності
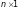 ,
а рівність означає рівність двох матриць
,
а рівність означає рівність двох матриць
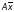 та
та
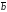 розмірності
розмірності
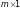 .
.
Приклад 1. Записати у матричному вигляді СЛР:
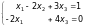
Очевидно,
матриця системи
 ,
стовпчик вільних членів
,
стовпчик вільних членів
 ,
отже, система у матричному вигляді
записується:
,
отже, система у матричному вигляді
записується:
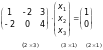 .
.
Очевидно, виконуючи операцію множення матриць, отримаємо початкову СЛР.
Однорідною
називається
система лінійних рівнянь, що має нульовий
стовпчик вільних членів,
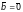 .
.
Неоднорідною називається система лінійних рівнянь, хоча б один елемент стовпчика вільних членів якої є ненульовим.
Розв’язком системи лінійних рівнянь, що містить n невідомих, називається впорядкований набір з n дійсних чисел – n-вимірний вектор , при підстановці яких в кожне рівняння системи замість відповідних змінних всі рівняння перетворюються на числові тотожності.
За множиною розв’язків системи поділяють на наступні види.
Система лінійних рівнянь називається сумісною, якщо має хоча б один розв’язок, та несумісною, якщо розв’язків не має.
Сумісна система лінійних рівнянь називається визначеною, якщо має єдиний розв’язок, та невизначеною, якщо розв’язків більше одного.
Проілюструємо введені поняття на системі з прикладу 1.
Очевидно,
система
є неоднорідною, сумісною (наприклад,
легко перевірити, що вектор
 є розв’язком системи) та невизначеною,
оскільки можна перевірити, що вектор
є розв’язком системи) та невизначеною,
оскільки можна перевірити, що вектор
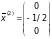 також є її розв’язком.
також є її розв’язком.
Зауваження. Очевидно, однорідна СЛР завжди сумісна, оскільки нульовий вектор завжди є її розв’язком.
2.2.Геометрична інтерпретація слр двох рівнянь з двома невідомими
Розглянемо СЛР
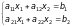 (2.3)
(2.3)
Очевидно,
розширена матриця цієї СЛР має вигляд
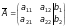 .
Позначимо визначники квадратних
підматриць другого порядку матриці
.
Позначимо визначники квадратних
підматриць другого порядку матриці
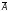 наступним чином:
наступним чином:
 ,
,
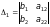 ,
,
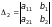 .
.
Геометричним образом кожного рівняння системи (2.3), очевидно, є прямі на площині x1Ox2, які ми позначимо l1 та l2; розв’язок системи (2.3) можна інтерпретувати як спільну точку цих прямих. Розглянемо всі можливі випадки для СЛР (2.3):
1)
СЛР (2.3) – несумісна
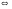
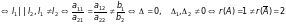 ;
;
2) СЛР (2.3) – сумісна та визначена
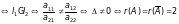 та
співпадає з кількістю невідомих;
та
співпадає з кількістю невідомих;
3) СЛР (2.3) – сумісна та невизначена
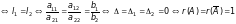 та
менший за кількість невідомих.
та
менший за кількість невідомих.
Ланцюги цих еквівалентностей показують зв’язок між системами лінійних рівнянь, їх геометричними образами, визначниками та рангами відповідних матриць.
Якщо СЛР містить три невідомі, то геометричним образом кожного рівняння буде площина у просторі (система з прикладу 1 задає перетин двох непаралельних площин який утворює пряму у просторі, тобто система сумісна та визначена), взаємне розташування яких, у загальному випадку, важко проаналізувати геометрично. З іншого боку, проаналізувати множину розв’язків таких систем можна на мові рангів відповідних матриць. Більш того, зв’язок між рангами матриць А, та множиною розв’язків СЛР, подібний наведеному в цих еквівалентностях, буде мати місце і для СЛР довільної розмірності, де геометрична інтерпретація стає неможливою.
