Гармонійний ряд
Гармонійним називається ряд
.
(14.11)
Цей ряд першим в історії математики був досліджений на збіжність. Необхідна умова збіжності виконується:
.
Але ще Я. Бернулі довів, що цей ряд є розбіжним.
Гармонійний ряд і геометрична прогресія найчастіше вибираються для порівняння згідно з теоремами 1 і 2. Також використовують узагальнений гармонійний ряд:
(14.12)
Він
збігається, якщо
,
і розбігається, якщо
.
Приклад 3. Дослідити на збіжність числовий ряд
.
Починаючи з другого члена, виконується нерівність
.
Ряд
є
геометрична прогресія. Її знаменник
,
так що прогресія збіжна. За теоремою 1
маємо, що досліджуваний ряд також є
збіжним.
Приклад 4. Дослідити на збіжність числовий ряд
.
Знайдемо
.
Необхідна
умова виконується, але
прямує до нуля як
,
тому що
.
Враховуючи це, виберемо як ряд порівняння
гармонійний ряд і застосуємо теорему
2:
,
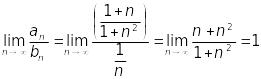Тобто досліджуваний ряд повинен бути розбіжним, бо гармонійний ряд розбігається.
Ознаки Даламбера, Коші, Маклорена-Коші
Ознака
Даламбера.
Якщо
,
починаючи з деякого номера, і існує
границя (скінчена або нескінчена)
,
(14.13)
то
при
ряд збігається, при
- розбігається. Якщо
,
то ознака не дає відповіді на питання
збіжності.
Приклад 5. Дослідити на збіжність числовий ряд
.
Зауважимо,
що
.
За ознакою Даламбера
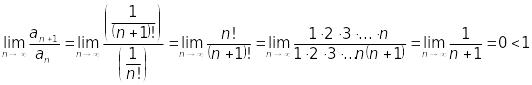
Тому ряд збігається.
Приклад 6. Дослідити на збіжність ряд
.
За ознакою Даламбера
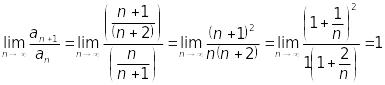
Ознака відповіді про збіжність чи розбіжність ряду не дає. Але за необхідною ознакою збіжності маємо
,
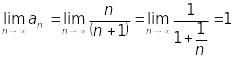
тобто ряд є розбіжним.
Радикальна ознака Коші. Якщо , починаючи з деякого номера, і існує границя (скінчена або нескінчена)
, (14.14)
то при ряд збігається, при - розбігається. При ознака відповіді на питання, розбіжний ряд чи збіжний, не дає.
Приклад 7. Дослідити на збіжність числовий ряд
.
За радикальною ознакою
,
тобто ряд збігається.
Інтегральна ознака Маклорена-Коші. Нехай члени ряду додатні і монотонно спадають:
і
- така неперервна монотонно спадна
функція, що
, тоді ряд і невласний інтеграл І-го роду
(14.15)
збігаються або не збігаються одночасно.
Приклад 8. Дослідити на збіжність числовий ряд
.
Члени ряду додатні і монотонно спадають:
.
Введемо
неперервну функцію
.
Тоді
.
Розглянемо невласний інтеграл
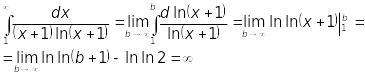
Інтеграл розбігається. Тому за ознакою Коші-Маклорена ряд також розбігається.
14.3. Знакозмінні ряди
Знакозмінним називається ряд, в якому є нескінченна кількість як додатних, так і від’ємних членів.
Якщо ряд (1) збігається одночасно з рядом з модулів
,
(14.16)
то ряд (14.1) називається абсолютно збіжним.
Якщо ряд (14.1) збігається, а ряд (14.16) розбігається, то ряд (14.1) називається умовно збіжним.
Теорема Коші. Щоб збігався знакозмінний ряд (14.1), достатньо, щоб збігався додатній ряд з модулів (14.16).
Ця умова не є необхідною для збіжності ряду, але коли вона виконується, ряд збігається абсолютно.
Ознака Лейбніца. Якщо знакозмінний ряд має вигляд
,
(14.17)
де
,
і його члени монотонно спадають за
абсолютною величиною, тобто
,
і існує границя
, (14.18)
то ряд збігається.
Ознака Лейбніца не дає відповіді на запитання, як збігається ряд: абсолютно чи умовно. Тут потрібне додаткове дослідження.
Приклад 9. Дослідити на умовну або абсолютну збіжність числовий ряд
.
По-перше, перевіримо, чи виконується необхідна умова збіжності:
.
Необхідна умова виконується. Модулі членів ряду утворюють монотонно спадну послідовність
.
Тому за ознакою Лейбніца ряд збігається. Щоб з’ясувати, умовно він збігається чи абсолютно, розглянемо ряд з модулів
.
Цей
ряд є частинним випадком узагальненого
гармонійного ряду (14.12), коли
.
При
ряд розбігається. Розбіжність легко
перевірити, використовуючи інтегральну
ознаку. Інтеграл
є розбіжним. Тому розглянутий знакозмінний ряд збігається умовно.
Приклад 10. Дослідити на умовну та абсолютну збіжність ряд
.
Очевидно,
що
.
Ряд з додатними членами
.
також
є узагальненим гармонійним рядом при
р=2. Ряд збігається, тому що
.
За першою теоремою порівняння буде
збіжним і ряд
.
Це ряд з модулів членів заданого знакозмінного ряду. За теоремою Коші його збіжність забезпечує абсолютну збіжність знакозмінного ряду.