Лекція 18: функціональні ряди

14.4.Область збіжності

Розглянемо послідовність , елементами якої є функції, визначені і неперервні в деякій області . З елементів функціональної послідовності складається функціональний ряд

(14.19)

При кожному фіксованому будемо мати числовий ряд. Значення , при якому ряд збігається, називається точкою збіжності ряду.

Сукупність усіх точок збіжності називається областю збіжності функціонального ряду.

Приклад 11. Визначити область збіжності функціонального ряду

.

Всі члени ряду визначені і неперервні на всій числовій прямій, крім точки х=-1. Якщо , то

і ,

тобто не виконується необхідна умова збіжності (14.8).

Якщо х=1, то і необхідна умова збіжності також не виконується.

Якщо , то даний ряд збігається абсолютно, бо збігається ряд з модулів. Це випливає з теореми порівняння. За теоремою 2 ряд з модулів поводить себе так само, як ряд з загальним членом .

Дійсно,

.

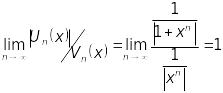Але ряд є геометричною прогресією із знаменником . З того, що , випливає, що знаменник менший за одиницю і прогресія збігається. Тобто наш ряд збігається абсолютно при .

Область збіжності: .

14.5.Правильна і рівномірна збіжність

Функціональний ряд (14.19) називається правильно збіжним в інтервалі , якщо його члени на цьому інтервалі задовольняють нерівності

. (14.20)

де , - числовий ряд з додатними членами, що збігається. Такий ряд називається мажорантою даного функціонального ряду.

Якщо ряд збігається правильно, то він збігається рівномірно.

Зворотне твердження в загальному випадку не виконується.

Приклад 12. Знайти область правильної збіжності функціонального ряду

.

Для всіх х буде виконуватись нерівність , тому мажорантою даного функціонального ряд буде числовий ряд , збіжність якого можна встановити за допомогою ознаки Коші:

.

З цього можна зробити висновок, що даний ряд збігається на всій числовій осі.

Функціональний ряд (19) називається рівномірно збіжним в області , якщо послідовність його частинних сум збігається рівномірно в цій області. Це буде за умови, якщо для будь-якого існує такий номер , що нерівність

(14.21)

справджується при всіх і всіх .

14.6.Ознака Вейєрштрасса

Якщо члени ряду (14.19) задовольняють нерівності (14.20)

для всіх , і числовий ряд з додатними членами збігається, то ряд збігається в області рівномірно.

Властивості рядів, що збігаються рівномірно

1. Неперервність суми ряду.

Якщо функції визначені і неперервні в деякій області і ряд (14.19) збігається в області рівномірно до суми , то ця сума буде неперервною в області .

2. Почленний перехід до границі.

Нехай кожна з функцій , де , визначена в області і має при скінчену границю

. (14.22)

Якщо в області рівномірно збігається ряд (19), то збігається і числовий ряд до суми С, а сума функціонального ряду також має границю при , причому

. (14.23)

3. Почленне інтегрування ряду.

Нехай ряд (14.19) збігається рівномірно в деякому проміжку до неперервної функції , а члени ряду , де , також неперервні в проміжку . Тоді ряд, утворений з інтегралів функцій, також збігається рівномірно до функції, яка дорівнює інтегралу від на ( ):

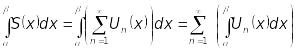. (14.24)

Тобто якщо ряд збігається рівномірно, то його можна почленно інтегрувати.

4. Почленне диференціювання ряду.

Нехай функції визначені в деякому проміжку і мають на ньому неперервні похідні . Якщо в цьому проміжку не тільки збігається ряд (19), але й рівномірно збігається ряд, створений з похідних,

, (14.25)

то сума ряду (19) має в похідну, яка дорівнює сумі ряду похідних.

Тобто при виконанні наведених умов стає можливим почленне диференціювання ряду

. (14.26)