Приклади розв’язуваня задач

Задача 1. Яку швидкість необхідно надати ракеті, щоб вона, стартувавши з поверхні Землі, не повернулася на Землю? Опір атмосфери не враховувати.

Розв’язування. З віддаленням ракети від Землі буде збільшуватися її потенціальна енергія і зменшуватися кінетична. За законом збереження енергії:

(1)

де m – маса ракети, M –маса Землі, G – гравітаційна стала v₀ і v – швидкості ракети відносно Землі в початковий і кінцевий моменти часу, R_З і R – відстані від центра Землі до ракети в початковий і розглянутий моменти, потенціал гравітаційного поля Землі на відстані R від її центру.

Після перетворення рівняння (1) маємо:

Ракета не повернеться на Землю, якщо її швидкість v буде в нескінченності дорівнювати нулю. тобто v=0 при . У цьому випадку маємо:

(2).

З закону всесвітнього тяжіння випливає, що на поверхні Землі

,

Відкіля

(3)

де g – прискорення вільного падіння на поверхні Землі.

Підставляючи формулу (2) у (3), знаходимо

.

Вважаючи, що ракета здобуває потрібну швидкість вже поблизу поверхні Землі, знаходимо:

Така швидкість необхідна для подолання гравітаційного поля Землі. Вона називається другою космічною або параболічною швидкістю.

Задача 2. Одноступінчаста ракета з початковою масою М_о = 3 т, включаючи запас палива m, виштовхує гази з швидкістю с = 3 км/сек. Нехтуючи впливом зовнішніх сил, визначити масу палива m, потрібну для досягнення першої космічної швидкості.

Розв'язання. Встановимо спочатку зв'язок між швидкістю ракети v та її масою М в довільний момент часу. Для цього скористаємось рівнянням Мещерського:

,

в якому припустимо, що F = 0:

.

Перепишемо останнє рівняння у вигляді:

,

скориставшись з того, що (знак мінус відповідає зменшенню М із зростанням часу).

Останнє співвідношення являє собою диференціальне рівняння з відокремленими змінними. Інтегруємо його:

.

Тут С – стала інтегрування, яку можна визначити з умови v = 0 при М = М₀, звідки , і, нарешті, знаходимо:

.

Позначимо величину першої космічної швидкості через = 7,9 км/сек. За умовою задачі, коли паливо буде повністю витрачено, тобто при М = М_о–m, повинно бути v=v₁. Підставляючи ці дані у останню формулу, знаходимо:

; ; m = 2,79 т.

Питання для перевірки знань

1. Момент імпульса і момент сили при обертальному русі точки по колу.

2. Основне рівняння динаміки обертального руху точки.

3. Рух тіла змінної маси. Вивід формули Ціолковського і рівняння Мещерського.

4. Рух планет і штучних супутників Землі. Закони Кеплера.

Задачі для розв’язування на практичних заняттях

1. Кулька, що прикріплена до нитки, довжина якої l=1 м, описує коло на горизонтальній площині. Який кут φ утворює нитка з вертикаллю, якщо частота обертання n=0,6 с^–1?

2. Літак виконує «мертву петлю» радіуса R=1 км. Визначити вагу P льотчика, маса якого m=70 кг, у момент коли швидкість літака V=720 км/год, а вектор швидкості v утворює кут α=45º з горизонталлю.

3. В елосипедист рухається зі швидкістю V=10 м/с по закругленню дороги радіуса R=15 м. Обчислити кут α нахилу велосипедиста до вертикалі, а також найменший коефіцієнт тертя ƒ між шинами велосипеда і дорогою, за яких забезпечується стійкість велосипедиста.

4. Тонка сферична оболонка, маса якої m=10 кг і радіус R=1 м, обертається з частотою ν=10 с 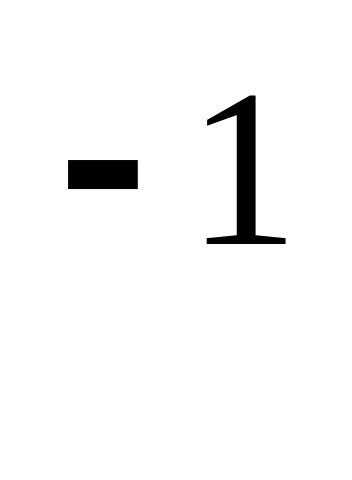навколо своєї осі симетрії. Визначити момент імпульсу L оболонки відносно цієї осі.

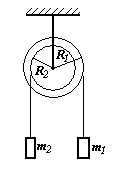
5. Визначити прискорення а вантажів і сили натягу Т ниток в системі, зображеній на рисунку, якщо m =2 кг, m 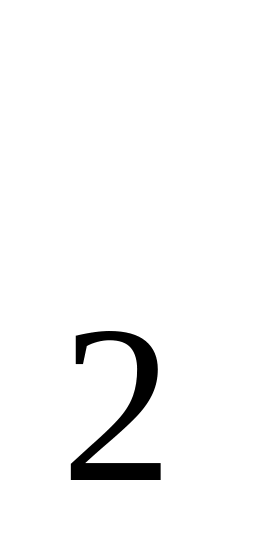=3 кг, R =20 см, R =10 см. Момент інерції східчастого блока відносно його осі I=0,05 кг·м². Нитки невагомі.