
- •6.100300 «Експлуатація суднових
- •Передмова
- •Мета роботи
- •Структура заняття
- •Вимоги до оформлення задач
- •1. Основні поняття кінематики. Кінематика поступального руху матеріальної точки.
- •Приклади розв’язування задач
- •Питання для перевірки знань
- •Задачі для розв’язування на практичному занятті
- •Задачі для самостійного розв’язування
- •Приклади розв’язування задач
- •Питання для перевірки знань
- •Задачі для розв’язування на практичному занятті
- •Задачі для самостійного розв’язування
- •Практичне заняття № 3 Тема: Динаміка руху точки по колу. Рух тіла зі змінною масою Теоретичні відомості
- •Приклади розв’язуваня задач
- •Питання для перевірки знань
- •Задачі для розв’язування на практичних заняттях
- •Задачі для самостійного розв’язування
- •Приклади розв’язування задач
- •Питання для перевірки знань
- •Задачі для розв’язування на практичних заняттях
- •Задачі для самостійного розв’язування
- •Практичне заняття № 5 Тема: Закон збереження імпульсу. Теорія пружних і непружних зіткнень Теоретичні відомості
- •Приклади розв’язування задач
- •Питання для перевірки знань
- •Задачі для розв’язування на практичному занятті
- •Задачі для самостійного розв’язування
- •Практичне заняття № 6 Тема: Динаміка обертального руху тіла. Умови рівноваги тіла Теоретичні відомості
- •Приклади розв’язування задач
- •Питання для перевірки знань
- •Задачі для розв’язування на практичному занятті
- •Задачі для самостійного розв’язування
- •Список рекомендованої літератури
Практичне заняття № 3 Тема: Динаміка руху точки по колу. Рух тіла зі змінною масою Теоретичні відомості
Нехай
частинка А, що має імпульс
![]() ,
рухається по дузі кола навколо точки
О. Положення точки характеризується
радіус-вектором
,
який спрямований до точки А з точки О.
Моментом
імпульсу
частинки А відносно точки О називають
вектор
,
рухається по дузі кола навколо точки
О. Положення точки характеризується
радіус-вектором
,
який спрямований до точки А з точки О.
Моментом
імпульсу
частинки А відносно точки О називають
вектор
![]() ,
який дорівнює векторному добутку
векторів
і
:
,
який дорівнює векторному добутку
векторів
і
:
![]() .
.
Напрямок вектора обраний так, що обертання навколо точки О в напрямку вектора і вектор утворять правогвинтову систему. Модуль вектора дорівнює:
![]() ,
,
де
– кут між векторами
і
,
![]() – плече вектора
щодо точки О.
– плече вектора
щодо точки О.
Знайдемо
величину, яка відповідає за зміну вектора
![]() в
даній системі відліку. Для цього
продиференціюємо формулу моменту
імпульсу за часом:
в
даній системі відліку. Для цього
продиференціюємо формулу моменту
імпульсу за часом:
![]() .
.
Так
як точка О нерухома, то вектор
![]() дорівнює швидкості
частинки, тобто збігається за напрямком
з вектором
,
тому
дорівнює швидкості
частинки, тобто збігається за напрямком
з вектором
,
тому
![]() .
.
Відповідно з другим законом Ньютона
![]() ,
,
де
![]() –
рівнодіюча всіх сил, прикладених до
частинки.
–
рівнодіюча всіх сил, прикладених до
частинки.
Отже,
![]() .
.
Моментом
сили
![]() щодо вісі обертання О називається
векторна фізична величина, яка дорівнює
векторному добутку радіус-вектора і
сили, що діє на точку:
щодо вісі обертання О називається
векторна фізична величина, яка дорівнює
векторному добутку радіус-вектора і
сили, що діє на точку:
![]() .
.
Напрямок
і модуль вектора
![]() визначається
так само, як і
:
визначається
так само, як і
:
![]() ,
,
де – плече сили .
Рівняння моментів: швидкість зміни моменту імпульсу частинки відносно деякої точки О обраної системи відліку дорівнює моменту рівнодіючої сили відносно тієї ж точки О:
![]() .
.
Якщо
система відліку є неінерціальною, то
момент сили
![]() містить
у собі як момент сил взаємодії, так і
момент сил інерції (відносно тієї ж
точки О).
містить
у собі як момент сил взаємодії, так і
момент сил інерції (відносно тієї ж
точки О).
М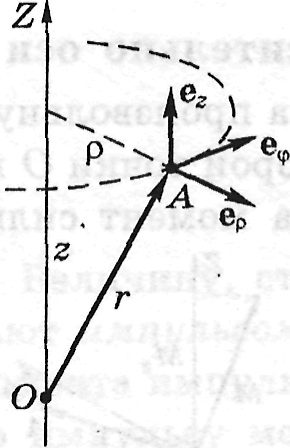 омент
імпульсу і момент сили відносно вісі.
Візьмемо в деякій системі відліку
довільну нерухому вісь Z. Нехай щодо
деякої точки О на вісі Z момент імпульсу
частинки А дорівнює
,
а момент сили, що діє на частинку,
.
Моментом
імпульсу відносно вісі Z
називають проекцію на цю вісь вектора
,
визначеного відносно довільної точки
О даної вісі. Моментом
сили відносно вісі Z
називають проекцію на цю вісь вектора
,
визначеного відносно довільної точки
О на вісі. Рівняння моментів у проекціях
на вісь Z буде мати вигляд:
омент
імпульсу і момент сили відносно вісі.
Візьмемо в деякій системі відліку
довільну нерухому вісь Z. Нехай щодо
деякої точки О на вісі Z момент імпульсу
частинки А дорівнює
,
а момент сили, що діє на частинку,
.
Моментом
імпульсу відносно вісі Z
називають проекцію на цю вісь вектора
,
визначеного відносно довільної точки
О даної вісі. Моментом
сили відносно вісі Z
називають проекцію на цю вісь вектора
,
визначеного відносно довільної точки
О на вісі. Рівняння моментів у проекціях
на вісь Z буде мати вигляд:
![]() .
.
Знайдемо
аналітичні вирази для проекцій моменту
імпульсу і моменту сили. Для цього
знайдемо проекцію на вісь Z векторних
добутків
![]() і
і
![]() .
Скористаємося циліндричною системою
координат ,
,
z,
зв'язавши з точкою А орти
.
Скористаємося циліндричною системою
координат ,
,
z,
зв'язавши з точкою А орти
![]() ,
які спрямовані убік зростання відповідних
координат. У цій системі координат
радіус-вектор
і
імпульс
частинки зображаються так:
,
які спрямовані убік зростання відповідних
координат. У цій системі координат
радіус-вектор
і
імпульс
частинки зображаються так:
![]() ,
,
![]() ,
,
де р, p, рz – проекції вектора на відповідні орти.
З векторної алгебри відомо, що векторний добуток може бути представлено визначником:
 ,
,
 ,
,
відкіля одержуємо формули для проекцій моменту імпульсу і моменту сили на вісь Z:
![]() ,
,
![]() ,
,
де
– найкоротша відстань частинки від
вісі Z. Так як проекція імпульсу частинки
на орт
![]() дорівнює
дорівнює
![]() ,
а
,
а
![]() ,
то в остаточному підсумку вираз для
моменту імпульсу здобуває вигляд:
,
то в остаточному підсумку вираз для
моменту імпульсу здобуває вигляд:
![]() .
.
Моментом інерції точки відносно довільної вісі обертання називається фізична величина, яка дорівнює добутку маси точки на квадрат найкоротшої відстані від вісі обертання до лінії, уздовж якої спрямований вектор імпульсу:
![]() .
.
З урахуванням останнього визначення формула для моменту імпульсу здобуває вигляд:
![]() .
.
Продиференціюємо останнє рівняння за часом:
![]()
або
![]() .
.
Отримане рівняння є другим законом Ньютона для руху точки по колу. У векторній формі воно має вигляд:
![]() .
.
Розглянемо
випадок, коли в процесі руху маса
матеріальної точки змінюється. Нехай
у деякий момент часу t маса тіла, що
рухається, m і її швидкість
.
Через деякий час
![]() маса
змінюється на
маса
змінюється на
![]() ,
а швидкість збільшиться на
,
а швидкість збільшиться на
![]() .
При цьому маса
,
що відокремилася, має швидкість
.
При цьому маса
,
що відокремилася, має швидкість
![]() щодо даного тіла. За ІІ законом Ньютона:
щодо даного тіла. За ІІ законом Ньютона:
![]() ,
,
де – рівнодіюча зовнішніх сил, що діють на тіло.
Зв'яжемо ІСВ з тілом у момент часу t. В обраній СВ тіло в момент початку спостереження знаходиться в стані спокою. Визначимо зміну імпульсу системи тіл:
![]() ,
,
![]() .
.
Розділимо отриманий вираз на dt:
![]() .
.
Так як , то після відповідної заміни одержуємо:
![]() .
.
Отримане
рівняння називають основним рівнянням
динаміки точки змінної маси або рівнянням
Мещерського.
![]() –
реактивна сила, яка виникає внаслідок
дії на тіло маси, що відокремлюється
або приєднується. Після замін одержуємо
основне рівняння динаміки при русі тіла
змінної маси:
–
реактивна сила, яка виникає внаслідок
дії на тіло маси, що відокремлюється
або приєднується. Після замін одержуємо
основне рівняння динаміки при русі тіла
змінної маси:
![]()
Окремі випадки застосування основного рівняння динаміки:
нехай
 .
У цьому випадку
.
У цьому випадку
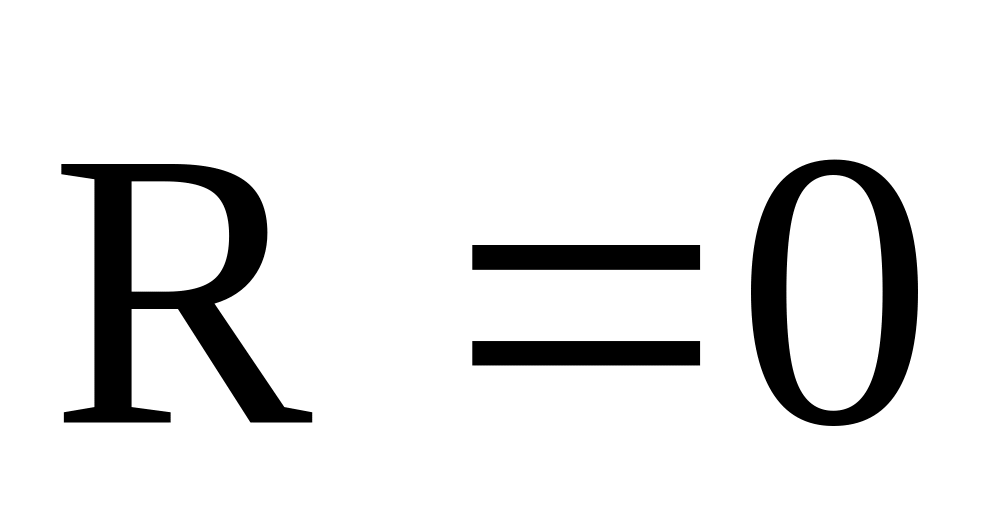 і основне рівняння динаміки приймає
вигляд:
і основне рівняння динаміки приймає
вигляд:
![]() ;
;
нехай система замкнена
 :
:
![]() ,
,
![]() ,
,
![]() .
.
Якщо у момент часу t тіло не рухається, то
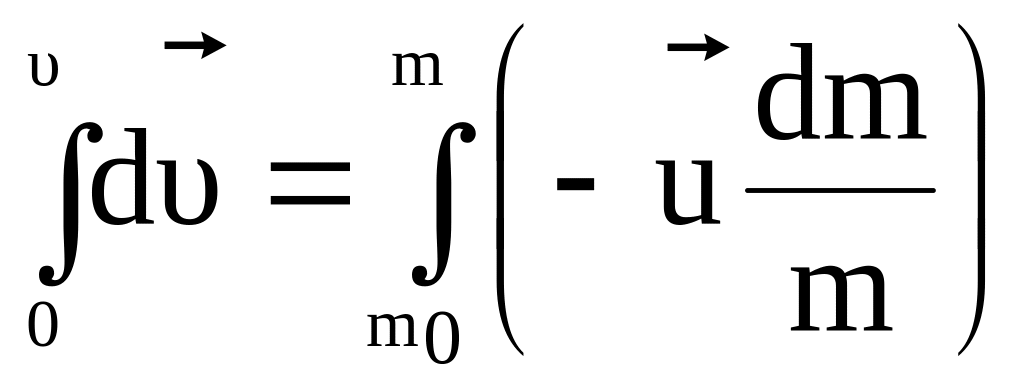 ,
,
![]() і
і
![]() – формула Ціолковського.
– формула Ціолковського.
З
формули Ціолковського випливає, що
швидкість ракети спрямована протилежно
швидкості вильоту газів (при
![]() ),
не залежить від часу згоряння палива,
а визначається тільки відношенням
початкової маси ракети до маси, що
залишилася.
),
не залежить від часу згоряння палива,
а визначається тільки відношенням
початкової маси ракети до маси, що
залишилася.
