Задачі для самостійного розв’язування

1. Рух матеріальної точки задано рівняннями: , , 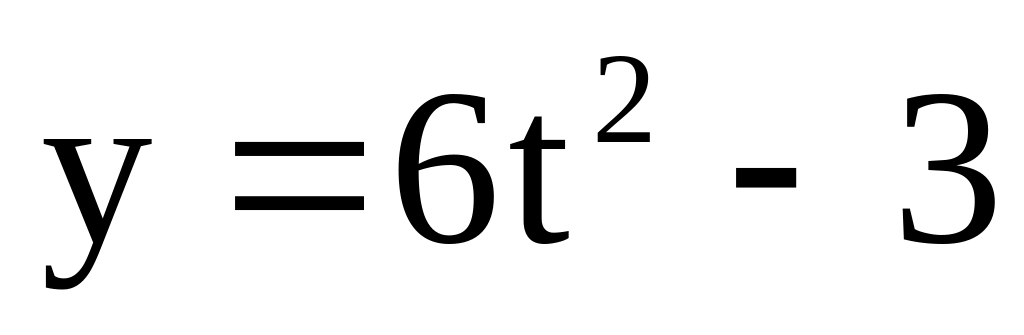z=0, де x, y, z – координати, м; t – час. Визначати модулі швидкості v і прискорення a точки.

2. Тіло кинуте вертикально вгору з початковою швидкістю v =21 м/с, було на половині свого найвищого підняття двічі. Визначити проміжок часу Δt між цими двома моментами.

3. Із однієї точки простору кидають два тіла горизонтально і вертикально вгору з однаковими швидкостями . на якій відстані 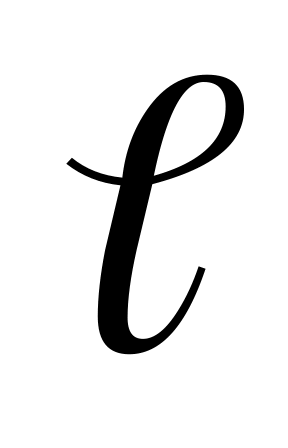перебуватимуть ці тіла через час t?

4. Через який час t після початку руху вектор швидкості тіла, що кинуто під кутом α=45° до горизонту з початковою швидкістю =10 м/с, утворюватиме з горизонтом кут β=30°?

Практичне заняття № 2

Тема: Кінематика обертального руху.

Використання законів динаміки для знаходження прискорення точки

Теоретичні відомості

Н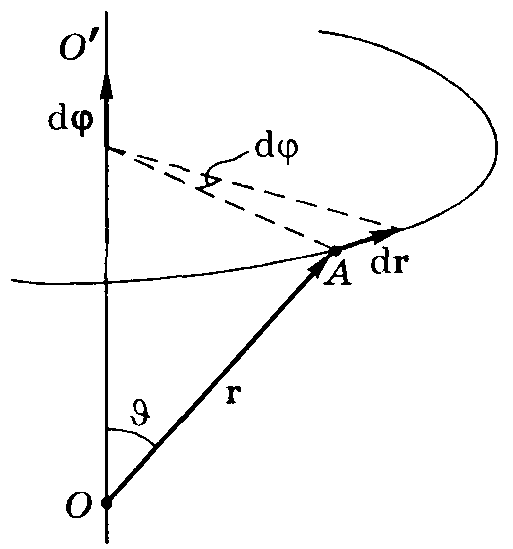 ехай радіус-вектор точки, що рухається по колу навколо нерухомої в даній системі відліку вісі , зробив за час dt нескінченно малий поворот.

Кут повороту d будемо характеризувати вектором , модуль якого дорівнює d, а напрямок збігається з віссю так, що напрямок повороту відповідає правилу "правило гвинта". Визначимо переміщення т. А за проміжок часу dt.

або у векторному вигляді .

Кутовою швидкістю обертання тіла називається фізична векторна величина, яка дорівнює відношенню зміни кута повороту до проміжку часу, протягом якого ця зміна відбулася:

, .

Напрямок збігається з , тобто визначається правилом правого гвинта.

Кутовим прискоренням називається фізична векторна величина, яка дорівнює відношенню зміни кутової швидкості до проміжку часу, протягом якого ця зміна відбулася:

, .

Н апрямок вектора збігається з напрямком . Запишемо формули та у проекціях на вісь Z, позитивний напрямок якої зв'яжемо з відліком координати  правилом правого гвинта:

, .

Визначимо залежність . Нехай :

, , , ,

, ,

О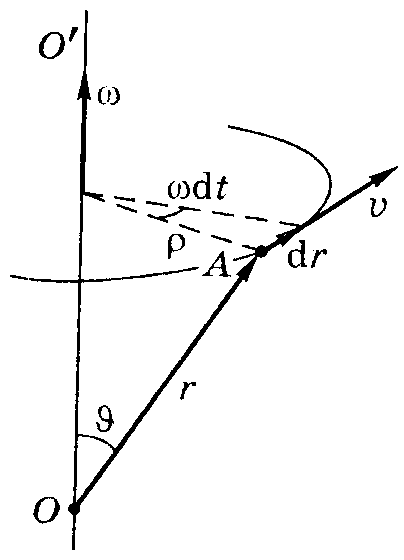 станнє рівняння називається рівнянням обертального руху матеріальної точки.

Визначимо швидкість довільної точки А, що обертається навколо нерухомої вісі ОО' з кутовою швидкістю . Нехай положення точки А відносно деякої точки О вісі обертання характеризується радіусом-вектором :

.

Розділимо обидві частини на dt:

.

У підсумку одержуємо:

або

.

Але – радіус кола, по який рухається точка. Після відповідних замін одержуємо формулу, що зв'язує лінійну і кутову швидкості:

.

Визначимо повне прискорення точки: продиференціюємо формулу :

,

, ,

де – тангенціальне прискорення, – нормальне прискорення.

Повне прискорення:

.

Модуль повного прискорення

.

Динаміка – розділ механіки, у якому розглядаються причини, що обумовлюють той чи інший характер руху тіла. В основу динаміки покладені 3 закони Ньютона.

І-й закон (Закон інерції Галілея): Існують такі системи відліку, відносно яких тіло, що рухається поступально, зберігає свою швидкість постійною, якщо на нього не діють інші тіла чи дія інших тіл компенсується.

Інерція – явище збереження швидкості тіла при відсутності зовнішніх впливів.

Системи відліку, у яких виконується явища інерції, називаються інерціальними. Для інерціальних систем відліку справедливий принцип відносності Галілея, згідно якого всі інерціальні СВ за своїми механічними властивостями еквіваленти одна іншій. Інакше кажучи, у всіх ІСВ всі закони механіки виконуються однаково.

Основні динамічні характеристики:

• Сила – векторна фізична величина, яка є кількісною мірою взаємодії тіл. Сила визначена, якщо задані її модуль, напрямок і точка дотикання.

• Рівнодіючою силою називається сила, що діє на тіло так само, як і всі сили, прикладені до нього. Вона дорівнює векторній сумі всіх сил, що діють на тіло. 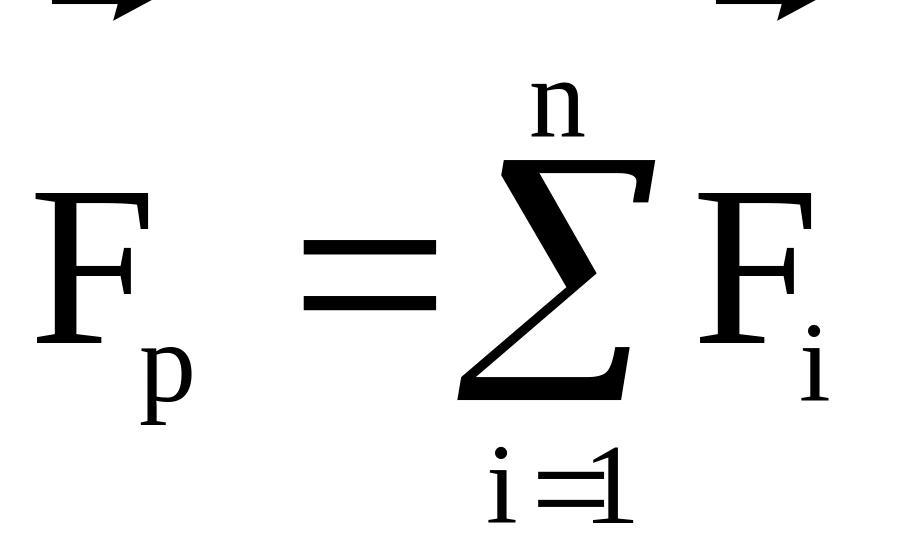. При дії сили тіло змінює свою швидкість або деформується.

• Маса – фізична величина, що є кількісною мірою інертності тіл. .

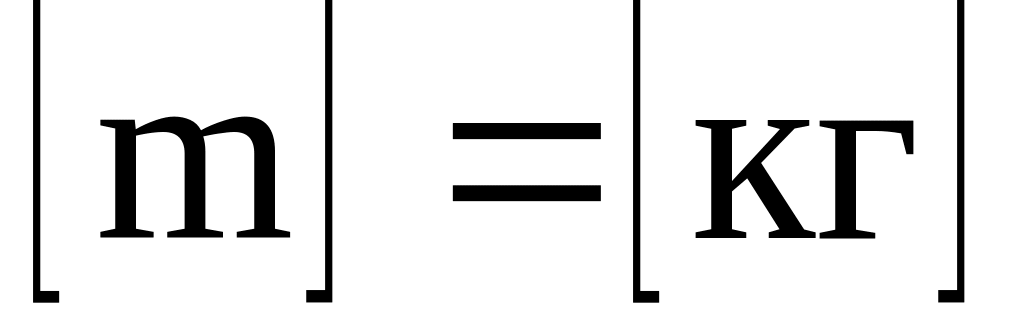• Інертність – властивість тіл, яка полягає у тім, що для зміни швидкості тіл потрібно якийсь час, чим більше цей час, тим більше інертне тіло.

Властивості маси:

а) адитивність, тобто маса складеного тіла дорівнює сумі мас окремих його частин;

б) маса тіла як цілого – величина постійна, що не змінюється при його русі.

• Імпульс чи тіла кількість руху – фізична величина, яка дорівнює добутку маси тіла на його швидкість. Напрямок збігається з напрямком .

.

• Імпульс сили – фізична величина, яка дорівнює добутку сили на час дії сили: , .

ІІ закон Ньютона.

Перше формулювання: прискорення тіла при взаємодії з іншими тілами, прямо пропорційно рівнодіючій силі, що діє на тіло і обернено пропорційно масі тіла.

.

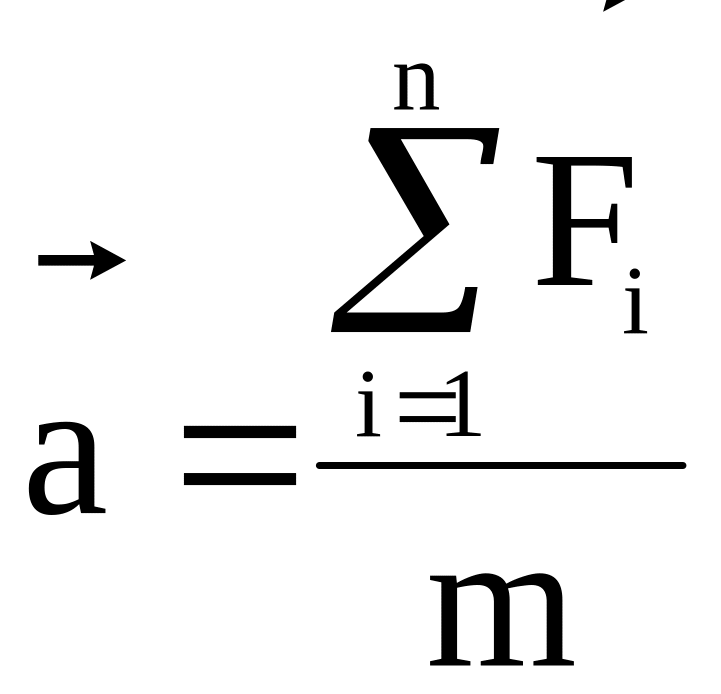Оскільки прискорення:

,

то після відповідної заміни одержуємо:

, .

Друге формулювання: швидкість зміни імпульсу тіла прямо пропорційна рівнодіючій силі, що діє на тіло.

ІІІ закон Ньютона: сили, з якими дві матеріальні точки взаємодіють між собою, завжди рівні за модулем, протилежні за напрямком, і спрямовані уздовж прямої, що з'єднують ці точки:

.

Особливості сил взаємодії:

• однієї природи;

• прикладені до різних матеріальних точок;

• виникають парами.

Основне рівняння динаміки матеріальної точки – математичний вираз другого закону Ньютона:

Розв’язування отриманого рівняння – основна задача динаміки матеріальної точки. При цьому можливі дві постановки задачі:

• знайти F, якщо відомі m і r(t).

• знайти закон руху точки, якщо відомі маса точки m, сила і визначені початкові умови ( 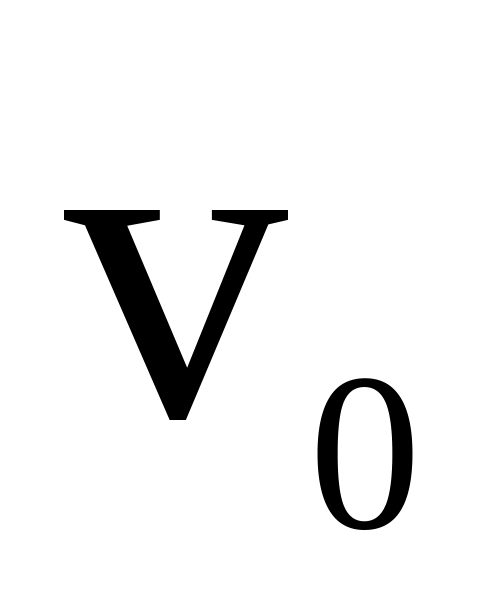та ).

Силові взаємодії в механіці поділяються на гравітаційні та електромагнітні.

Гравітаційні здійснюються між тілами відповідно до закону Всесвітнього тяжіння. Електромагнітні виникають між тілами або частинками, що мають електричний заряд.

Закон Всесвітнього тяжіння: сили взаємодії двох матеріальних точок прямо пропорційні добутку мас цих точок і обернено пропорційні квадрату відстані між ними.

,

де  – гравітаційна стала:  = 6,67*10^–11 (Н*м²)/кг². До сил гравітаційної природи відносять вагу тіла.

Вага тіла – це сила, з яким тіло діє на опору чи підвіс, що нерухомі відносно даного тіла. За ІІІ законом Ньютона вага дорівнює силі реакції опори або силі пружності підвісу:

.

Сили електромагнітної природи.

Пружна сила – сила, пропорційна зміщенню матеріальної точки з положення рівноваги і спрямована до положення рівноваги:

,

де – радіус-вектор, який характеризує зміщення частинки з положення рівноваги, k – коефіцієнт, що характеризує пружні властивості тіла. Цей закон називають законом Гука.

Сила тертя – виникає на межі контакту тіл і спрямована протилежно напрямку передбаченого руху тіл. Тертя підрозділяють на тертя спокою, тертя ковзання і тертя катання.

Сила тертя спокою – дорівнює проекції зовнішніх сил на лінію контакту L тіл:

.

Тертя ковзання – виникає при ковзанні одного тіла на поверхні іншого і спрямовані в протилежному напрямку руху тіла. Знаходиться за формулою:

,

де – коефіцієнт тертя ковзання, що залежить від природи і стану дотичних поверхонь, N – сила нормальної реакції поверхні.

Сила тертя катання. Виникає з тієї причини, що точка опори зміщується уперед внаслідок деформації поверхонь, і момент сили тяжіння перешкоджає вільному руху тіла. Знаходиться за формулою:

,

де R – радіус тіла, що котиться.

Сила опору – сила, що діє на тіло при його русі в рідині чи газі. При невеликих швидкостях:

,

де k – коефіцієнт опору.