Приклади розв’язування задач

Задача 1. Рух тіла масою 1 кг задано рівнянням s=6t³+3t+2. Знайти залежність швидкості і прискорення від часу. Обчислити силу, що діє на тіло наприкінці другої секунди.

Розв’язування. Миттєву швидкість знаходимо як похідну від шляху за часом: ; . Миттєве прискорення визначається першої похідної від швидкості за часом чи другою похідною від шляху за часом: Сила, що діє на тіло, визначається за другим законом Ньютона: F = ma, де а – прискорення наприкінці другої секунди. Тоді

Відповідь: v = 18t²+3; a = 36t; F=72H.

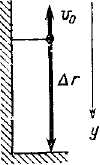
Задача 2. Кулька, що кинута з балкона у вертикальному напрямку, через t = 3 с упала на Землю. Визначити початкову швидкість кульки, якщо висота балкона над Землею дорівнює 14,1 м. Опором повітря зневажити,

Розв’язування. В умові не зазначений напрямок, у якому кинуто кульку, – вертикально вниз або вгору. Однак ця невизначеність не є істотною для рішення задачі. У будь-якому випадку рух м'яча буде рівноприскореним із прискоренням вільного падіння, а висота балкона над Землею, яка дана в умові задачі, цілком визначає вектор переміщення кульки (див. малюнок). Тому для рішення задачі досить скористатися рівнянням рівноприскореного руху:

. (1)

Припустимо, що кулька кинута зі швидкістю вертикально вгору. Направимо вісь проекцій У вертикально вниз. Дотримуючи правила знаків, одержимо

.

Розв’язуючи останнє рівняння відносно , остаточно отримуємо:

.

Позитивний знак величини показує, що початкова швидкість кульки спрямована саме так, як ми припустили, тобто вертикально вгору.

Легко переконатися в тім, що вибір позитивного напрямку осі відліку довільний, Так, направивши вісь У вгору, одержимо рівняння:

З якого випливає попередній результат.

Якщо припустити, що початкова швидкість спрямована вертикально вниз, то будемо мати

.

Розв’язавши це рівняння, знайдемо v₀ = – 10 м/с. Негативний знак показує, що насправді початкова швидкість кульки спрямована не так, як ми припустили, а вертикально вгору, тобто прийшли до колишнього результату.

Питання для перевірки знань

1. Види механічного руху. Траєкторія, шлях, переміщення.

2. Середні і миттєві кінематичні величини (визначення, формули, одиниці вимірювань).

3. Основна задача механіки. Розв’язування ОЗМ для рівноприскореного руху.

4. Рух точки відносно різних систем відліку. Закон додавання швидкостей та прискорень.

5. Способи завдання положення точки у просторі.

Задачі для розв’язування на практичному занятті

1. Матеріальна точка рухається прямолінійно. Залежність пройденого шляху від часу описується рівнянням 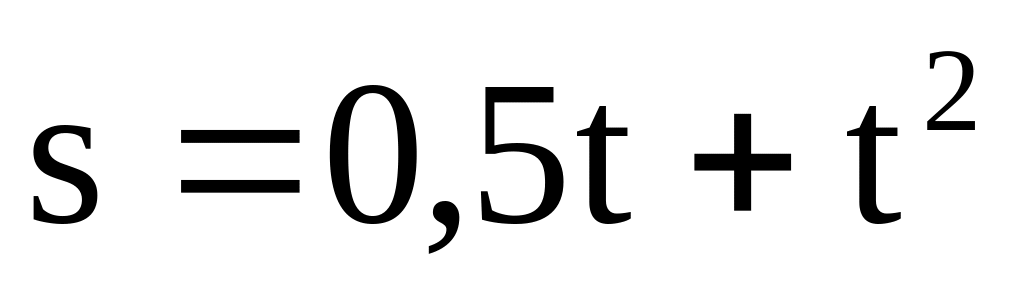, де s – шлях, м; t – час, с. Визначити залежність швидкості v і прискорення a від часу, середню швидкість за другу секунду руху та шлях s, який пройшла точка за п’яту секунду.

2. На висоті =100 м тіло, що вільно падає, мало швидкість 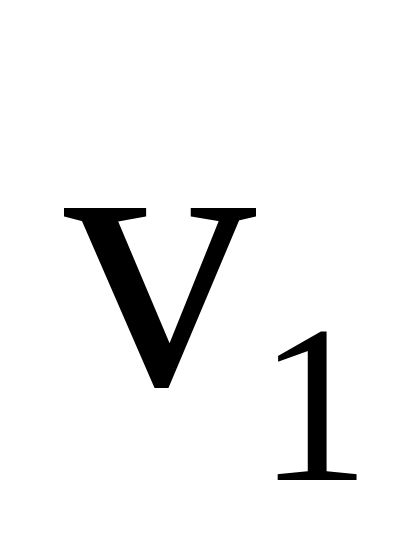=20 м/с. Чому дорівнюватиме швидкість тіла на висоті 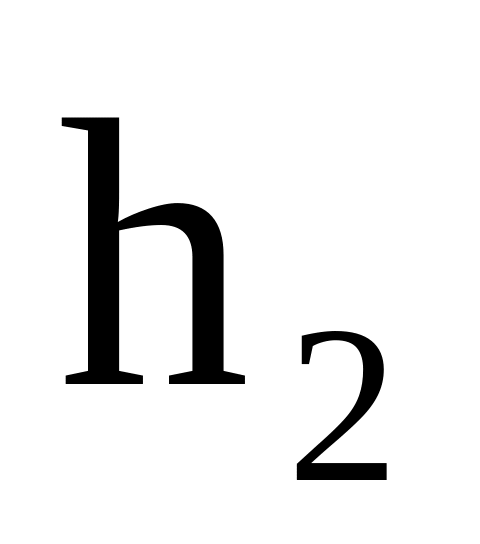=75 м?

3. Тіло кинуто з поверхні землі під кутом α=30° до горизонту з початковою швидкістю 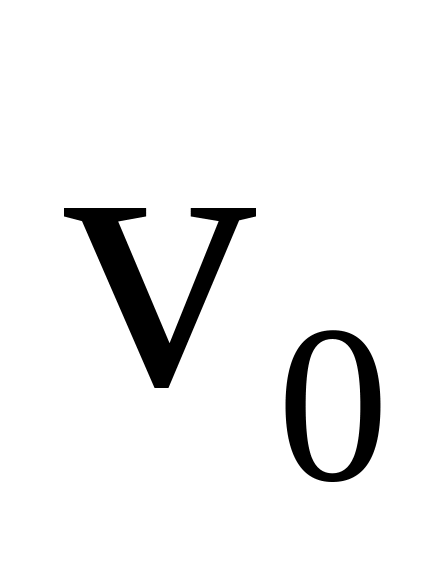=10 м/с. Нехтуючи опором повітря, встановити: швидкість тіла v в момент часу =0,8 с; рівняння траєкторії; час підйому 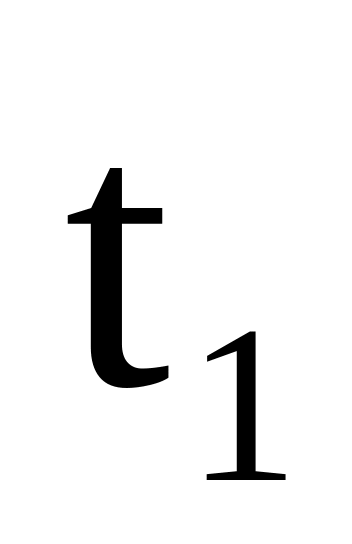і час падіння 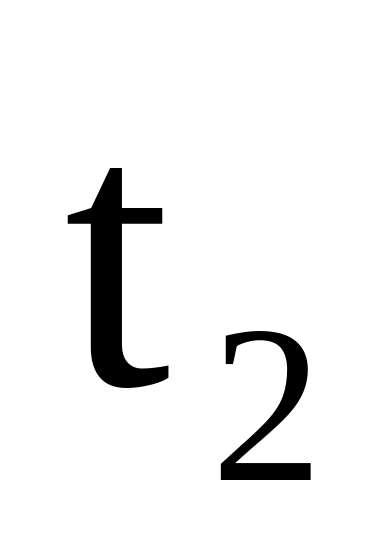; дальність s польоту; радіус кривизни R траєкторії в момент часу .

4. Швидкість частинки змінюється за законом 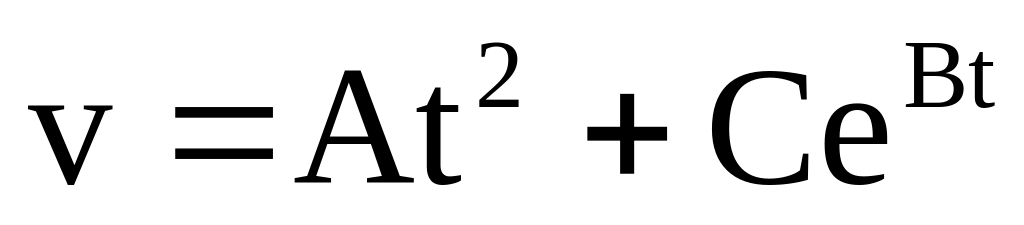, де А=3 м/с³, В=1с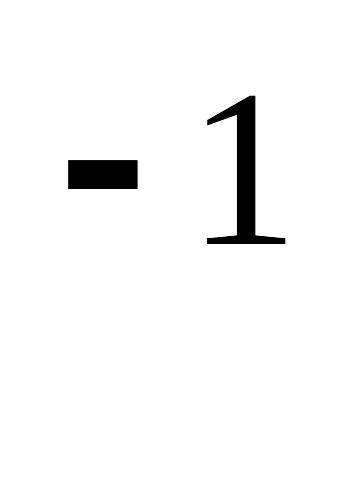 , С=1м/с. Обчислити прискорення а частинки наприкінці першої секунди руху, шлях s, пройдений частинкою і середню швидкість за цей час.

5. Тіло кинуте вертикально вгору з початковою швидкістю v =21 м/с, було на половині свого найвищого підняття двічі. Визначити проміжок часу Δt між цими двома моментами.