Задачі для самостійного розв’язування

1. Вантаж прив’язали до нижнього кінця вертикальної пружини, верхній кінець якої закріплений на штативі. З положення, що відповідає недеформованій пружині, вантаж підтримуючи рукою, повільно опускають до положення рівноваги. При цьому пружина розтягується на довжину l=5 см. на яку довжину l розтягнеться пружина, якщо вантаж опускатиметься вільно з того самого положення?

2. Кулька, яка котиться без ковзання по горизонтальній поверхні зі швидкістю V =5 м/с, стикається по нормалі зі стіною. Вважаючи, що удар пружний, обчислити швидкість V кульки після відбивання в момент часу, коли вона почне рухатися без ковзання.

3. З вершини сферичної поверхні радіуса R скочується без проковзування маленька кулька. На якій висоті h над центром сфери кулька відділиться від поверхні сфери й полетить вільно?

4. Куля, швидкість якої V =10 м/с, закочується без проковзування на похилу площину. На яку висоту h підніметься куля?

Практичне заняття № 6 Тема: Динаміка обертального руху тіла. Умови рівноваги тіла Теоретичні відомості

Розглянемо тверде тіло, яке може обертатися навколо вісі обертання і рухатися поступально. Його рух у загальному випадку визначається двома векторними рівняннями:

• рівняння руху центра мас:

;

• рівняння моментів у Ц-системі:

.

Знаючи закони діючих зовнішніх сил, точки їхнього прикладу і початкові умови, можна за допомогою цих рівнянь знайти як швидкість, так і положення кожної точки твердого тіла в будь-який момент часу, тобто цілком розв’язати задачу про рух тіла.

Умови рівноваги твердого тіла.

Тіло буде залишатися в стані спокою, якщо відсутні причини, що викликають його рух. Для цього необхідно і достатньо виконання двох умов:

1. рівнодіюча всіх зовнішніх сил, які прикладені до тіла, повинна бути рівною нулю:

;

2. сумарний момент зовнішніх сил відносно будь-якої точки теж повинний бути рівним нулю:

.

Ц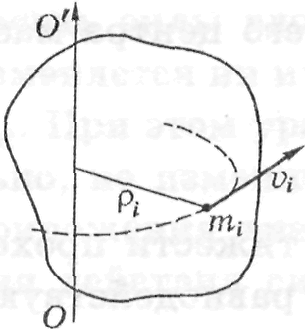 і умови повинні виконуватися в тій системі відліку, де тіло знаходиться в стані спокою. Якщо система відліку неінерціальна, то крім зовнішніх сил взаємодії треба враховувати і сили інерції. Це ж відноситься і до моментів сил.

Обертання тіла навколо нерухомої вісі.

Нехай тверде тіло обертається навколо нерухомої вісі. Визначимо вираження для моменту імпульсу твердого тіла відносно вісі обертання ОО'. Момент імпульсу тіла може бути представлений таким чином:

,

де і – маса і відстань від вісі обертання і-ї частинки твердого тіла, – його кутова швидкість.

Величина в дужках являє собою момент інерції твердого тіла відносно вісі ОО':

.

З останньої формули випливає, що момент інерції твердого тіла залежить від розподілу мас щодо цікавлячої нас вісі і є величиною аддитивною. Обчислення моменту інерції тіла проводиться за формулою:

,

де dm і dV – маса й об’єм елемента тіла, що знаходиться на відстані r від цікавлячої нас вісі Z,  – густина тіла в даній точці.

Якщо задано момент інерції відносно вісі, що проходить через центр мас, момент інерції відносно будь-якої вісі, паралельної даної і віддаленої від неї на відстань а, визначається за теоремою Штейнера: Момент інерції відносно довільної вісі Z дорівнює моментові інерції І_с відносно вісі Z_с, що паралельна даної і проходить через центр мас С тіла, плюс добуток маси m тіла на квадрат відстані а між вісями:

.

Рівняння динаміки обертання твердого тіла.

Нехай тверде тіло обертається навколо нерухомої вісі. Проекція моменту імпульсу в цьому випадку визначається за формулою:

.

Продифференціюємо останнє рівняння за часом:

або .

З останнього рівняння свідчить, що момент інерції визначає інерційні властивості твердого тіла при обертанні: при тому самому значенні моменту сил тіло з великим моментом інерції здобуває менше кутове прискорення.

Інтегрування отриманого рівняння з урахуванням початкових умов дозволяє цілком розв’язати задачу про обертання твердого тіла навколо нерухомої вісі, тобто знайти залежності кутової швидкості і кута повороту від часу.

Нехай  = const. Тоді , , . У підсумку рівняння залежності проекції кутової швидкості від часу має вигляд:

.

З формули кутової швидкості випливає:

, .

Після інтегрування одержуємо рівняння обертального руху твердого тіла:

.

Робота зовнішніх сил при обертанні твердого тіла навколо нерухомої вісі.

При обертанні твердого тіла навколо нерухомої вісі обертання потенціальна енергія залишається сталою, тому робота всіх зовнішніх сил дорівнює зміні тільки кінетичної енергії тіла:

.

Оскільки , то після підстановки одержуємо:

, ( ,

так як вісь Z за напрямком збігається з кутовою швидкістю). Тоді

і .

Відповідно до основного рівняння динаміки обертального руху твердого тіла

.

Підставляючи останню формулу у вираження для механічної роботи і враховуючи, що

,

одержуємо:

.

Робота зовнішніх сил при повороті на кінцевий кут дорівнює . У випадку, якщо , остання формула спрощується:

.

Висновок: Робота зовнішніх сил при обертанні твердого тіла навколо нерухомої вісі визначається дією моменту цих сил відносно даної вісі. Якщо сили такі, що їхній момент , то роботи вони не виконують.

Плоский рух твердого тіла.

При плоскому русі центр мас С твердого тіла рухається у визначеній площині, що нерухома в даній К-системі відліку, а вектор його кутової швидкості увесь час залишається перпендикулярним до цій площині. Останнє означає, що в Ц-системі тверде тіло виконує чисто обертальний рух навколо нерухомої в цій системі вісі, що проходить через центр мас тіла. Обертальний рух твердого тіла визначається рівнянням , яке справедливо в будь-якій системі відліку.

Таким чином, плоский рух твердого тіла може бути описаним наступними двома рівняннями:

, ,

де m – маса тіла, F – рівнодіюча всіх зовнішніх сил, і – момент інерції і сумарний момент усіх зовнішніх сил відносно вісі, що проходить через центр мас тіла.

Інтегруючи отримані рівняння з урахуванням початкових умов, можна знайти залежності и , що визначають положення твердого тіла в будь–який момент t.

Кінетична енергія при плоскому русі твердого тіла.

Кінетична енергія при плоскому русі твердого тіла складається з енергії обертання в Ц–системі і енергії, що зв'язана з рухом центра мас:

.