Приклади розв’язування задач

Задача 1. На двох шнурах однакової довжини, яка дорівнює 0,8 м, підвішені дві свинцевих кулі масами 0,5 і 1 кг. Кулі стикаються між собою. Кулю меншої маси відвели убік так, що шнур відхилився на кут  = 60°, і відпустили. На яку висоту піднімуться обидві кулі після зіткнення? Удар вважати центральним і непружним. Визначити енергію, яка витрачається на деформацію куль при ударі.

Р озв’язування. Оскільки удар куль непружний, то після удару кулі будуть рухатися з загальною швидкістю v. Закон збереження імпульсу при цьому ударі має вигляд:

(1)

Тут v₁ і v₂ – швидкості кульок до удару. Швидкість великої кулі до удару дорівнює нулю. Швидкість меншої кулі знайдемо використовуючи закон збереження енергії. При відхиленні меншої кулі на кут  вона здобуває потенціальну енергію, яка потім переходить у кінетичну:

.

Із рисунка видно, що

,

Тому

. (2)

З рівнянь (1) і (2) знаходимо швидкість куль після удару:

. (3)

Кінетична енергія, яку мають кулі після удару, переходить у потенціальну:

(4)

де h – висота, на яку піднімуться кулі після зіткнення.

З формули (4) знаходимо

.

Враховуючи (3), отримаємо:

, .

При иепружньому ударі куль частина енергії витрачається на їхню деформацію. Енергія деформації знаходиться як різниця кінетичних енергій до і після удару:

.

Використовуючи рівняння (2) і (3), одержуємо:

, .

Задача 2. Молот масою 70 кг падає з висоти 5 м і вдаряє по залізному виробу, що лежить на ковадлі. Маса ковадлі разом з виробом 1330 кг. Вважаючи удар абсолютно непружним, визначити енергію, що витрачається на деформацію виробу. Систему вважати замкнутою.

Розв’язування. За умовою задачі система молот-виріб-ковадло вважається замкнутою, а удар непружний. За законом збереження енергії можна вважати, що енергія, яка витрачена на деформацію виробу, дорівнює різниці значень механічної енергії системи до і після удару. Вважаємо, що під час удару змінюється тільки кінетична енергія тіл, тобто незначним переміщенням тіл по вертикалі під час удару зневажаємо. Тоді для енергії деформації виробу маємо:

(1)

де v – швидкість молота наприкінці падіння з висоти h, v’ – швидкість тіл системи після непружнього удару.

Швидкість молота наприкінці падіння визначається без врахування опору повітря і тертя за формулою

. (2)

Загальну швидкість тіл системи після непружнього удару знайдемо за допомогою закону збереження імпульсу:

(3)

Для розглянутої системи закон збереження імпульсу має вигляд:

,

відкіля знаходимо:

(4)

Підставивши у формулу (1) вираження (2) і (4), одержимо:

.

Питання для перевірки знань

1. Зовнішні і внутрішні сили. Імпульс системи тіл Закон збереження імпульсу системи тіл (з виводом).

2. Повна механічна енергія системи в зовнішнім полі. Закон збереження повної механічної енергії.

3. Зв'язок між енергіями в К- і Ц-системах відліку.

4. Теорія пружних і непружних зіткнень.

Задачі для розв’язування на практичному занятті

1. Кулька масою m =0,01 кг, що має швидкість V =500 м/с, пробиває кулю масою m=5 кг, яка висить на нитці. При цьому швидкість кульки зменшилася до V =100 м/с. Яка частина η енергії кульки перейшла в теплоту?

2. К 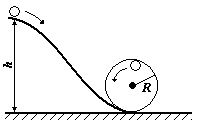улька, маса якої m=50 г, скочується без проковзування з висоти h=30 см і описує вертикальну петлю радіуса R=10 см (см. малюнок). З якою силою кулька тиснена жолоб у нижній і верхній точках петлі по нормалі до неї?

3. Кулька скочується по похилому жолобу, який описує вертикальну петлю радіуса R (см. малюнок). З якої мінімальної висоти h має рухатися кулька, щоб не відірватися від жолоба у верхній точці петлі? Розглянути два випадки: а)кулька зісковзує; б) кулька скочується.

4. Куля, маса якої m=10 г, рухаючись зі швидкістю V=500 м/с, влучає в ціль. З якою середньою силою F діяла куля на ціль, якщо вона проникла в неї на глибину l=1 см? Втратами енергії на нагрівання і руйнування матеріалу нехтувати.

5. Куля, маса якої m =200 г, має швидкість V =20 м/с і налітає на нерухому кулю масою m =100 г. Внаслідок центрального удару втрати механічної енергії Q=5 Дж. Визначити швидкості куль U та U після їх зіткнення.

6. Кулька, маса якої m=1 кг, ударяється об стіну під кутом α=60º до нормалі зі швидкістю V =10 м/с, а відскакує від неї зі швидкістю V =6 м/с під кутом β=45º. Визначити модуль імпульсу p, що дістала стіна. Яка кількість теплоти Q виділиться під час удару?