
- •18.2. Проектний розрахунок валів
- •Порядок проектного розрахунку.
- •18.3. Перевірний розрахунок валів на міцність
- •Значення коефіцієнта Кd і Кd
- •Значення коефіцієнта впливу шорсткості поверхні кf
- •Числові значення ефективних коефіцієнтів концентрації напруги згинання к і крутінні к
- •18.4. Розрахунок валів на жорсткість
- •Формули для визначення прогинів y і кутів нахилу поперечного перерізу θ валів постійного перерізу
- •18.5. Розрахунок валів на коливання
- •18.6. Розрахунок осей. Проектний розрахунок
- •Контрольні запитання
- •19. Підшипники ковзання
- •19.1. Призначення і класифікація підшипників
- •19.3. Конструкція та матеріали підшипників ковзання
- •19.5. Практичний розрахунок підшипників ковзання
- •Допустимі значення [p], [pv] та [V]
- •Динамічна в’язкість μ·106 (н·с/мм2) деяких мастил при різних температурах tºC
- •20. Підшипники кочення
- •20.1. Загальні відомості
- •20.2. Класифікація, матеріали деталей підшипників, їх точність
- •20.4. Основні критерії роботоздатності та розрахунку підшипників кочення
- •20.5. Підбір підшипників кочення за статичною вантажопідйомністю
- •Значення коефіцієнтів радіального та осьового статичного навантаження однорядних підшипників
- •20.6. Підбір підшипників кочення за динамічною вантажопідйомністю
- •20.7. Еквівалентне динамічне навантаження
- •Значення коефіцієнтів радіальної X та осьової y сил підшипників кочення
- •20.7. Ресурс підшипників кочення
- •Рекомендує мий ресурс підшипників кочення для деяких машин і обладнання
- •Коефіцієнт еквівалентного навантаження khe
- •20.8. Особливості розрахунків навантаження радіально-упорних підшипників
- •Контрольні запитання
- •21. 0Порні вузли валів редукторів
- •21.1. Схеми установки підшипників
- •21.2. Типові опорні вузли валів редукторів
- •2 Рис. 21.5. Опорні вузли вала черв’яка: а - за схемою “врозпір”; б – з фіксуючою опорою 1.3. Кріплення підшипників на валах
- •21.4. Кріплення підшипників у корпусі
- •Контрольні запитання
18.5. Розрахунок валів на коливання
Під дією зовнішніх сил, які діють постійно або періодично змінюються і зв’язані із пружною деформацією, виникають коливання валів. Якщо частота коливання валів досягає будь-якої власної частоти, наступає резонанс системи, і навіть незначні коливання навколо положення рівноваги стають небезпечними для роботоздатності вала. На практиці спостерігаються крутильні (кутові), згинальні (поперечні) і згинально-крутильні коливання.
1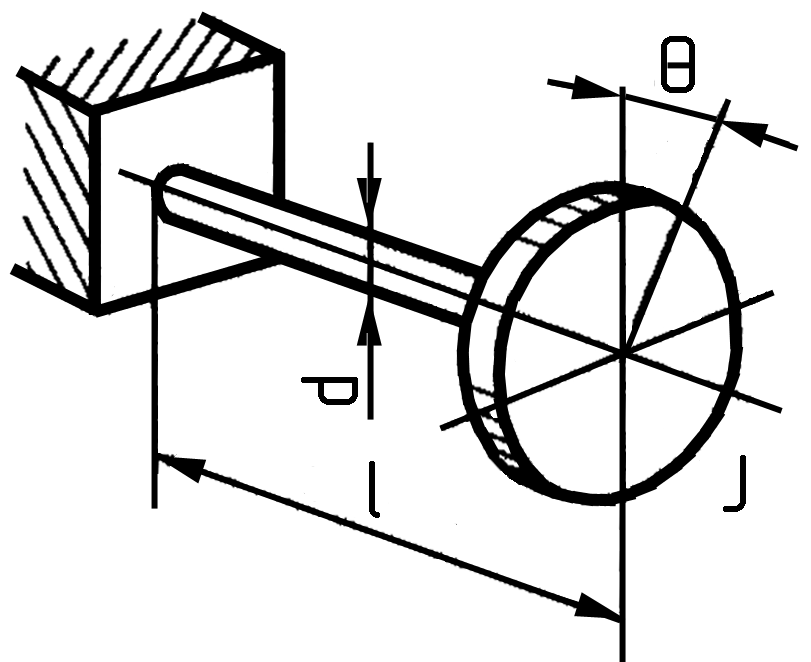 8.5.1.
Крутильні коливання виникають
в валах поршневих машин (двигунах
внутрішнього згорання, поршневих
компресорах і т.п.) і зв’язані із
нерівномірністю в часі обертового
моменту або моменту опору. Основною
задачею розрахунку
крутильних
коливань є визначення власних частот
системи для виявлення резонансних
обертів.
8.5.1.
Крутильні коливання виникають
в валах поршневих машин (двигунах
внутрішнього згорання, поршневих
компресорах і т.п.) і зв’язані із
нерівномірністю в часі обертового
моменту або моменту опору. Основною
задачею розрахунку
крутильних
коливань є визначення власних частот
системи для виявлення резонансних
обертів.
Р
Рис.
18.10.
Розрахункова
схема крутильних коливань вала
![]() (18.14)
(18.14)
де Jm - момент інерції маси диска, кгсм2; - кут повороту, рад.; Т - момент, який діє на диск, Нм.
Знак - в рівнянні (18.14) вказує на те, що момент Т створюється силами пружності, що перешкоджає відхиленню. Якщо жорсткість вала позначити через с, причому ця величина являє собою момент в Нсм необхідний для закрутки вала на 1 рад., то
![]() (18.15)
(18.15)
Із урахуванням рівняння (18.15) із рівняння (18.14) одержуємо:
![]()
Загальний інтеграл цього рівняння має такий вид:
![]() (18.16)
(18.16)
де р - колова частина коливань, с-1;
![]() (18.17)
(18.17)
Довільні постійні А і В визначають із вихідної умови.
Якщо в момент t
= 0,
а,
![]() ,
то
,
то
![]() (18.18)
(18.18)
де а - амплітудне значення кута повороту при коливаннях.
Момент інерції Jm для диска:
![]() кгм2
(18.19)
кгм2
(18.19)
де М - маса диска, кг.
Для деталей складної форми момент інерції визначають експериментально.
Жорсткість прямолінійного вала
![]() (18.20)
(18.20)
де
![]() - модуль пружності матеріалу на зсування,
для сталей G
= (0,78...0,83)105
МПа; Jр
- полярний момент інерції перерізу, для
суцільного вала
- модуль пружності матеріалу на зсування,
для сталей G
= (0,78...0,83)105
МПа; Jр
- полярний момент інерції перерізу, для
суцільного вала
![]() якщо переріз послаблено шпонковим пазом
або шліцами, то
якщо переріз послаблено шпонковим пазом
або шліцами, то
![]() (h -
глибина канавки; k
= 0,5 - для одного шпонкового пазу, k
= 1 - для двох шпонкових пазів, розміщених
під кутом 90,
k = 1,2 -
для двох шпонкових пазів, розміщених
під кутом 180,
k =
1,8 - для шліцьових валів).
(h -
глибина канавки; k
= 0,5 - для одного шпонкового пазу, k
= 1 - для двох шпонкових пазів, розміщених
під кутом 90,
k = 1,2 -
для двох шпонкових пазів, розміщених
під кутом 180,
k =
1,8 - для шліцьових валів).
18.5.2. Згинальні коливання зв’язані з деформацією згинання стержнів, наприклад, такі коливання мають осьові компресори, лопатки турбін тощо.
Р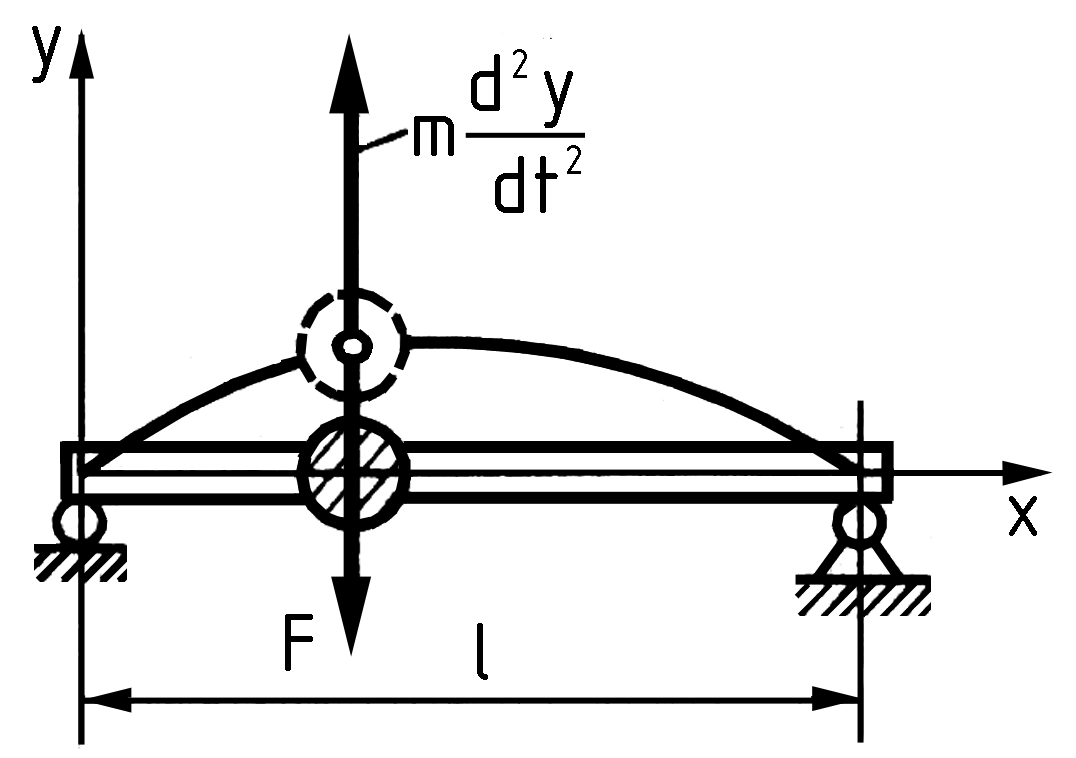 озглянемо
одномасову систему, яка являє собою
коливання вантажу на невагомому стержні
(рис.18.11).
озглянемо
одномасову систему, яка являє собою
коливання вантажу на невагомому стержні
(рис.18.11).
Рівняння руху маси m:
Рис.
18.11. Розрахункова
схема згинальних коливань одномасної
системи деталей вала![]() (18.21)
(18.21)
де F - сила пружності;
![]() (18.22)
(18.22)
де - прогин балки в місці прикладання вантажу під дією одиничної сили, так званий коефіцієнт податливості.
Із рівняння (18.21) одержуємо:
![]() (18.23)
(18.23)
Вирішив рівняння, знайдемо формулу для визначення колової частоти згинальних коливань р:
![]() (18.24)
(18.24)
Це рівняння справедливе для будь-якої одномасової системи; вантаж може бути розміщеним між опорами або консольно - різниця лише в величині .
Рішення рівняння (18.23) при довільних вихідних умовах буде таким:
![]() (18.25)
(18.25)
де у0 - амплітуда коливань; - зсув фази, який залежить від початкових умов.
Якщо підставити рішення (18.25) в рівняння (18.23), то одержимо:
![]() (18.26)
(18.26)
Це рівняння аналізується
так: сила пружності
![]() дорівнює інерційному навантаженню
дорівнює інерційному навантаженню
![]() ,
тобто другими словами – амплітудний
прогин у0
викликається силою р2mу0.
,
тобто другими словами – амплітудний
прогин у0
викликається силою р2mу0.
1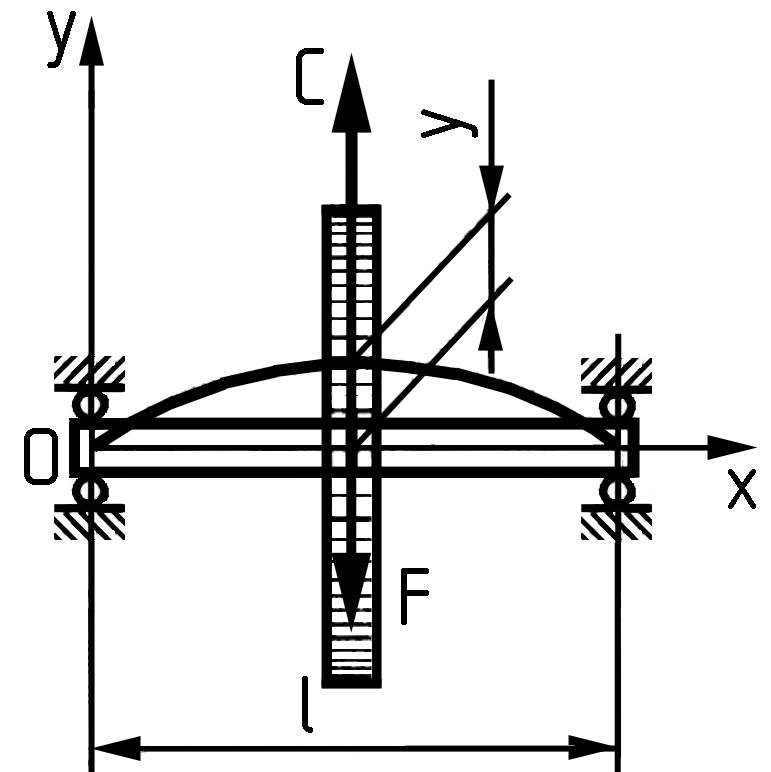 8.5.3.
Критичні частоти обертання валів.
Розглянемо вал на двох опорах з диском
посередині (рис. 18.12), який обертається
із кутовою швидкістю .
Нехай вал одержить деяке відхилення і
центр тяжіння почав рухатися по колу
радіусом у.
Тоді на диск буде діяти відцентрова
сила С і
сила пружності F:
8.5.3.
Критичні частоти обертання валів.
Розглянемо вал на двох опорах з диском
посередині (рис. 18.12), який обертається
із кутовою швидкістю .
Нехай вал одержить деяке відхилення і
центр тяжіння почав рухатися по колу
радіусом у.
Тоді на диск буде діяти відцентрова
сила С і
сила пружності F:
![]()
![]() (14.27)
(14.27)
д
Рис.
18.12.
Вал на двох опорах з диском посередині
![]() (18.28)
(18.28)
Якщо С F, то після відхилення вал знову вернеться в початкове положення, тобто прямолінійне положення осі є стійким.
В момент рівноваги, тобто в момент початку втрати стійкості, коли С F, прогини можуть необмежено зростати. В цьому випадку відцентрові сили у відхиленому положенні дорівнюють силам пружності, які намагаються вернути вал у вихідний стан. Частоти обертання, при яких наступає рівність відцентрових сил і сил пружності, називається критичними.
При критичному значенні величина С = F, звідки:
![]()
![]() (18.29)
(18.29)
Можна вважати, що при критичній частоті обертання кр вал повністю втрачає жорсткість на згинання; навіть дуже мала сила може визвати значні прогини.
Із рівняння (18.29) виходить, що критична кутова швидкість кр співпадає із коловою частотою згинальних (поперечних) коливань р. Цей висновок справедливий і в загальному випадку, якщо деталі, що закріплені на валі, розглядають як точкові маси.
В дійсності прогини при = кр залишаються конечними, так як завжди існують обмеження (защемлення в підшипниках, тертя тощо), і, крім того, при великих деформаціях порушується лінійна залежність між силою і переміщенням.
Однак, наближення кутової швидкості до критичної кр може бути небезпечним, і тому зону частот обертання від n = (0,7...1,3) nкр не рекомендується використовувати для робочих режимів.
У всіх випадках бажано працювати із жорсткими роторами (валами) для яких 0,7кр. Робота вала з одним диском можлива і при кр, але при цьому часто необхідно використовувати спеціальні демпфіруючи опори для проходження через критичні частоти і для заспокоєння вібрацій в за критичній області.
Якщо вал має декілька дисків, і відповідно декілька критичних кутових швидкостей кр1, кр2,...,кр.п, то критичний стан наступає при співпаданні кутової швидкості із будь-якою із критичних швидкостей.
Для стійкої роботи вала діапазон частот обертання
0,7кр.і 1,3кр.і (і = 1, 2,..., n)
рекомендується вимогами із робочих режимів.
