Глава 2.Решение модельной задачи
Если параметры модели, входящие в дифференциальные уравнения, начальные и граничные условия, являются функциями координат и времени, то получить её решение в аналитическом виде в общем случае нельзя.
Параметры задачи могут зависеть от искомой функции, тогда уравнение называется квазилинейным. Такие уравнения также не удаётся решить аналитически в общем случае. Только при некоторых специфических зависимостях параметров могут быть аналитически найдены частные решения. Но таких случаев немного. В ещё большей степени сказанное относится к нелинейным уравнениям.
Поэтому единственным универсальным подходом является численное решение уравнений математической модели. Используются два мощных метода численного решения дифференциальных уравнений (ДУ):
- метод конечных разностей (МКР);
- метод конечных элементов (МКЭ).
Общим для обоих методов является то, что они, в конечном итоге, сводятся к замене краевой задачи для дифференциального уравнения системой линейных алгебраических уравнений (СЛАУ) или системой нелинейных уравнений (СНУ). Решением СЛАУ ил СНУ является конечномерный вектор значений искомой функции (решения ДУ) в точках, определённым образом выбранных из области её определения. Эти точки называются узлами, совокупность всех узлов образует сетку. Значения функции между узлами получают интерполированием.
Различие между МКР и МКЭ заключается в способе перехода от ДУ к СЛАУ или СНУ.
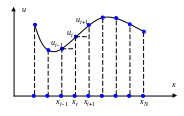
МКР базируется на замене производных в ДУ разностными отношениями. В одномерном случае они могут, например, иметь вид (рис.2.1)
,
где
,
,
- узловые точки.
Рис.2.1 Аппроксимация производных
Коэффициенты
и неоднородные члены ДУ также вычисляются
в точках
или в промежуточных точках на интервале
или
.
В результате приходим после приведения
подобных членов к СЛАУ
(2.1)
где
- матрица,
- вектор значений искомой функции в
узлах,
- вектор правых частей. Знак
обозначает операцию транспонирования.
МКЭ исходит из противоположной идеи. Вместо исходного ДУ формулируется эквивалентная задача минимизации некоторого функционала, называемого функционалом энергии. Например, краевой задаче
(2.2)
соответствует функционал энергии
(2.3)
Область
определения функции
разбивается на конечные
элементы
(КЭ), в которых она и коэффициенты
уравнения непрерывны. Сама функция
в пределах конечного
элемента аппроксимируется полиномом.
Реально используют линейную или (реже)
квадратичную аппроксимацию. В одномерном
случае линейный полином имеет вид
(2.4)
где
- значения функции в узлах. При большем
числе измерений конечный элемент может
быть задан несколькими способами.
Например, для двумерных задач область
определения можно разбить на треугольники
(рис.2.2а), а можно – на четырёхугольники
(рис.2.2б).
Рис. 2.2 Разбиение на конечные элементы
В
любом случае значения функции
внутри КЭ должны быть выражены через
её значение в узлах. Если подставить
аппроксимацию (2.4) в (2.3) и выполнить
интегрирование, получим функционал
энергии
как
функцию неизвестных
.
Минимизируя его относительно каждого
неизвестного условием
придём
к СЛАУ
(2.5)
Таким образом, оба метода сводят дифференциальную задачу к алгебраической. Каждый их них обладает достоинствами и имеет недостатки.
МКР проще в постановке задачи. Для его успешной реализации требуется лишь правильный выбор сетки и разностной аппроксимации. Этот вопрос давно исследован теоретически, сформулированы правила построения экономичных в смысле затрат компьютерных ресурсов алгоритмов. Недостатком МКР является сложность представления граничных условий и учёта неоднородности и анизотропии параметров задачи.
В МКЭ постановка задачи может оказаться достаточно сложной, требующей высокой квалификации и опыта для удачного выбора КЭ и аппроксимаций. Но зато он позволяет создавать универсальные программы, пригодные для решения задач с неоднородными и анизотропными параметрами. В силу этого свойства МКЭ приобрёл в последние десятилетия большую популярность. Он лежит в основе практически всех прикладных программ для расчётов в области гидродинамики, прочности, электродинамики, тепломассообмена.
В настоящем лабораторном практикуме для численного решения краевых задач для дифференциальных уравнений применяется МКР.
Чтобы найти N-мерный вектор - решение СЛАУ (3.1) или соответствующей СНУ – необходимо, во-первых, выбрать или разработать алгоритм нахождения решения, а, во-вторых, реализовать его в виде компьютерной программы. Алгоритм есть последовательность действий, посредством которых находится решение. Эти действия обязательно включают:
- задание (определение) числовых параметров модели;
- задание функциональных зависимостей модели;
- вычисление коэффициентов СЛАУ или СНУ;
- вычисление вектора решения;
- представление решения в наглядной графической форме.
К
аждое
из перечисленных действий может, в свою
очередь, состоять из последовательности
действий. Действия эти могут быть
безальтернативными, выполняемыми
последовательно, либо альтернативными,
выполняемыми в зависимости от результата
проверки некоторого условия. При наличии
альтернатив алгоритм содержит
разветвления. Частным случаем разветвления
является многократное повторение
однотипных вычислений, называемое
циклом.
Завершённый цикл можно рассматривать
как одно действие. Алгоритм полезно
представить в виде блок-схемы, состоящей
из четырёх типов элементов, соединённых
стрелками: прямоугольник - для
безальтернативных действий; ромб - для
проверки условия; овал - для обозначения
начала и конца программы; окружность
- для результата проверки условия.
Блок-схема программы решения СЛАУ (3.1)
может иметь вид (рис. 3.3). Заполнение
отдельного блока производиться средствами
конкретного программного продукта. Мы
будем использовать в качестве рабочего
инструмента программы MathCAD
и Matlab.
Они содержат обширные библиотеки
встроенных функций, решающих стандартные
математические задачи – вычисление
интегралов, сумм, нахождение решений
ДУ, СЛАУ и СНУ, вычисление значений
функций, операции с матрицами и т.п.
Поэтому, например, блок нахождения
решения
может состоять из
обращения к соответствующей функции.
Но в некоторых случаях может потребоваться
разработка оригинального алгоритма.
Блочное представление алгоритма позволяет чётче уяснить его логику, усовершенствовать и оптимизировать её, и, в конечном счёте, лучше понять смысл соответствующей математической модели, как говориться, «почувствовать» её.
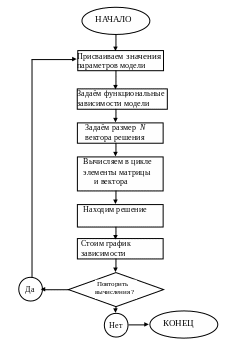
Рис. 2.3 Типовая блок-схема алгоритма