
- •Ю.П. Головатый, в.Г. Косушкин
- •Глава 6. Численное решение краевых задач для обыкновенных дифференциальных уравнений
- •Глава 7. Численное решение задач на собственные значения
- •Глава 8. Численное решение дифференциальных уравнений в частных производных
- •Глава 1. Формулировка математической модели
- •1.1. Тепловой баланс резистивного элемента
- •1.2. Радиационно-стимулированная диффузия
- •Глава 2.Решение модельной задачи
- •Глава 3. Метод конечных разностей
- •3.1. Сетки и сеточные функции
- •3.2. Аппроксимация производных
- •Конечноразностная аппроксимация обыкновенных дифференциальных уравнений
- •Глава 4. Решение задачи коши методом конечных разностей
- •Методы эйлера и тейлора
- •4.2 Явные методы рунге - кутты
- •4.3 Явные многошаговые методы решения задачи коши.
- •Лабораторная работа №3
- •4.4 Подвохи при применении методов рунге-кутты
- •«Жёстские» обыкновенные дифференциальные уравнения
Глава 1. Формулировка математической модели
Формулировка математической модели объекта или процесса состоит из следующих действий.
1.Конкретизация геометрии задачи. Это подразумевает определение пространственной области, в которой протекают исследуемые процессы, наличия у неё элементов симметрии, соотношения размеров. Эта информация используется для упрощения задачи путём понижения её размерности и выбора наиболее удобной системы координат.
2.Вывод уравнений модели. Уравнения модели выводятся из интегральных законов сохранения, вариационных принципов и законов движения применительно к конкретной ситуации. Чаще всего модель включает дифференциальные уравнения. Изредка оказывается целесообразным исходить непосредственно из интегрального соотношения. Так, например, задача о распределении имплантированных ионов в полубесконечном полупроводнике формулируется в виде интегрального уравнения для функции распределения. В других случаях приходится иметь дело с интегро-дифференциальными уравнениями.
Значительным облегчением является то, что многие широко используемые в прикладных науках уравнения давно известны и изучены. Поэтому в большинстве случаев надо не выводить, а просто использовать подходящее уравнение. Но в некоторых случаях вывод целесообразно произвести заново, а иногда уравнение приходится даже постулировать на основе интуитивной догадки. Анализ модельного уравнения значительно упрощается, если его преобразовать к безразмерной форме посредством выбора подходящих переменных. При этом естественным образом возникают масштабные величины, численные значения которых определяют поведение решения.
3.Задание начальных и граничных условий. Начальные условия ставятся для нестационарных задач. Они отражают состояние исследуемого объекта или процесса в момент начала его изучения. Граничные условия отражают взаимодействие объекта с окружающей средой в течение всего времени исследования. Физически взаимодействие может заключаться в заданном движении граничных точек объекта, отражать характер переноса через границу массы, энергии, импульса.
Проиллюстрируем изложенную технологию двумя примерами.
1.1. Тепловой баланс резистивного элемента
Сформулируем
математическую модель, описывающую
распределение температуры вдоль
резистивного элемента цилиндрической
формы длиной L
и радиусом
![]() .
Пусть в холодном состоянии, при температуре
окружающей среды
.
Пусть в холодном состоянии, при температуре
окружающей среды
![]() ,
его удельное электросопротивление и
коэффициент теплопроводности равны
,
его удельное электросопротивление и
коэффициент теплопроводности равны
![]() и
и
![]() соответственно. Между концами элемента
создаётся разность потенциалов
соответственно. Между концами элемента
создаётся разность потенциалов
![]() .
При протекании тока в объёме выделяется
омическое тепло. Часть его идет на
разогрев резистивного элемента, другая
часть теряется через торцы и боковую
поверхность. Торцевые потери определяются
граничными условиями. Поверхностные
потери происходят по конвективному и
лучистому механизмам в соответствии с
законами Ньютона и Стефана-Больцмана
соответственно. Вследствие неравенства
их можно трактовать как объёмные
потери, обусловленные объёмными
теплостоками, мощность которых
определяется локальной температурой
.
При протекании тока в объёме выделяется
омическое тепло. Часть его идет на
разогрев резистивного элемента, другая
часть теряется через торцы и боковую
поверхность. Торцевые потери определяются
граничными условиями. Поверхностные
потери происходят по конвективному и
лучистому механизмам в соответствии с
законами Ньютона и Стефана-Больцмана
соответственно. Вследствие неравенства
их можно трактовать как объёмные
потери, обусловленные объёмными
теплостоками, мощность которых
определяется локальной температурой
![]() элемента объёма
элемента объёма
![]() (рис. 2.1). Приближение состоит в том, что
температура считается одинаковой по
всему сечению элемента. Это позволяет
свести задачу к одномерной.
(рис. 2.1). Приближение состоит в том, что
температура считается одинаковой по
всему сечению элемента. Это позволяет
свести задачу к одномерной.

Рис. 2.1 Баланс энергии в резистивном элементе
Баланс
энергии в объёме
![]() в стационарном состоянии можно записать
в виде
в стационарном состоянии можно записать
в виде
![]() (1.1)
(1.1)
Прибыль
тепловой энергии происходит вследствие
её притока
![]() через сечение
через сечение
![]() и выделения в объёме
и выделения в объёме
![]() ,
где
,
где
![]() - объёмная плотность омических источников
теплоты. Убывает тепловая энергия
вследствие её оттока
- объёмная плотность омических источников
теплоты. Убывает тепловая энергия
вследствие её оттока
![]() через сечение
через сечение
![]() ,
конвективных потерь
,
конвективных потерь
![]() и лучистых потерь
и лучистых потерь
![]() через боковую поверхность
через боковую поверхность
![]() .
Таким образом, имеем уравнение
.
Таким образом, имеем уравнение

которое,
после сокращения на S
и предельного перехода
![]() ,
преобразуется к виду
,
преобразуется к виду
![]() (1.2)
(1.2)
Здесь
![]() - универсальная постоянная Стефана-Больцмана,
- универсальная постоянная Стефана-Больцмана,
![]() - степень черноты боковой поверхности,
h
- постоянная конвективного теплообмена
с размерностью
- степень черноты боковой поверхности,
h
- постоянная конвективного теплообмена
с размерностью
![]() .
Плотность омических источников тепла
найдём из определения
.
Плотность омических источников тепла
найдём из определения
![]()
где
![]() - сопротивление элемента объёма dV,
I
- ток. Откуда
- сопротивление элемента объёма dV,
I
- ток. Откуда
![]()
В
однородном резистивном элементе
![]() и
и
![]() зависят от координаты только через
температуру,
зависят от координаты только через
температуру,
![]()
В
широком интервале температур зависимость
![]() линейная,
линейная,
![]()
где
![]() – термический коэффициент сопротивления.
Ток одинаков в любом сечении и равен
– термический коэффициент сопротивления.
Ток одинаков в любом сечении и равен
![]()
где
R
- полное
сопротивление элемента при данном
распределении температуры
![]() ,
,
![]()
Таким образом, Q явно зависит только от T,
 (1.3)
(1.3)
Коэффициент
теплопроводности
![]() с ростом температуры убывает по степенному
закону
с ростом температуры убывает по степенному
закону
![]() или
или
 ,
где
,
где
![]() .
.
В
уравнении (1.2) удобно перейти к безразмерным
переменным
![]() ,
,
![]() ,
,
 (1.4)
(1.4)
В
(1.4) появились комбинации параметров,
определяющие поведение решения
![]() :
:
![]() -
характерная объёмная плотность тепловой
мощности,
-
характерная объёмная плотность тепловой
мощности,
![]() -
характерная объёмная плотность омических
потерь.
-
характерная объёмная плотность омических
потерь.
Поделив все слагаемые уравнения (2.4) на , приведём его к виду
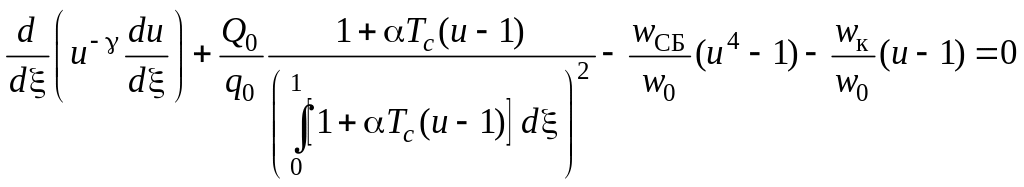
(1.5)
где введены новые характерные параметры с размерностью плотностью потока энергии:
![]() -
характерная плотность теплового потока,
-
характерная плотность теплового потока,
![]() -
характерная плотность лучистого потока,
-
характерная плотность лучистого потока,
![]() -
характерная плотность конвективного
потока энергии.
-
характерная плотность конвективного
потока энергии.
Знаменатель
во втором слагаемом превращает (1.5) в
интегро-дифференциальное уравнение.
Решать его можно только итерационно,
что не очень приятно. Но можно упростить
задачу, заметив, что для данного элемента
среднее значение удельного сопротивления
![]() зависит только от U,
причём так, что
зависит только от U,
причём так, что
![]() при
при
![]() .
Если эту зависимость аппроксимировать
подходящей функцией, например,
двухпараметрической,
.
Если эту зависимость аппроксимировать
подходящей функцией, например,
двухпараметрической,

где
![]() и
и
![]() - эмпирические параметры, то уравнение
(1.5) превращается в дифференциальное
- эмпирические параметры, то уравнение
(1.5) превращается в дифференциальное
 (1.6)
(1.6)
Граничные условия на торцах определяются типом контакта. Например, при лучисто-конвективном теплообмене с внешней средой граничные условия имеют вид
 (1.7)
(1.7)
или, в безразмерной форме,
 (1.8)
(1.8)
Определив
характерный поверхностный тепловой
поток
![]() ,
представим (1.8) в виде
,
представим (1.8) в виде
 (1.9)
(1.9)
Сделаем
численные оценки характерных параметров
для вольфрамового резистивного элемента
длиной
![]() и радиусом
и радиусом
![]() при
разности потенциалов
при
разности потенциалов
![]() .
.
Исходные параметры:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Характерные параметры:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Таким образом, в уравнение (1.6) и граничные условия (1.9) войдут пять безразмерных параметров,
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Из
равенства
![]() для данного конкретного случая следует,
что уже при
для данного конкретного случая следует,
что уже при
![]() лучистые потери через боковую поверхность
в 5 раз превосходят конвективные потери,
поэтому соответствующими слагаемыми
в уравнении (1.6) и граничных условиях
(1.9) можно пренебречь. Математическая
модель, описывающая температурный
режим вольфрамового резистивного
элемента, состоит из уравнения
лучистые потери через боковую поверхность
в 5 раз превосходят конвективные потери,
поэтому соответствующими слагаемыми
в уравнении (1.6) и граничных условиях
(1.9) можно пренебречь. Математическая
модель, описывающая температурный
режим вольфрамового резистивного
элемента, состоит из уравнения
![]() (1.10)
(1.10)
и граничных условий
 (1.11)
(1.11)
