«Жёстские» обыкновенные дифференциальные уравнения
Существует класс ОДУ, для численного решения которых явные методы абсолютно непригодны. Это так называемые «жёсткие» уравнения. Их решения содержат быстро меняющиеся и медленно меняющиеся компоненты. Таково, например, уравнение
,
общее решение которого суть
Если, в соответствии
с условием устойчивости, взять шаг
,
то время счёта окажется большим, притом,
что компонента решения
затухает чрезвычайно быстро, и во всей
области определения доминирует медленная
компонента
.
Но увеличить шаг при использовании
явной схемы нельзя, так как при этом
возникает быстрая “разболтка” численного
решения (рис. 4.4). На рисунке показаны
линейные переходы с одной интегральной
кривой на другую. Видно, что “приближённое”
решение
очень быстро удаляется от исходной
интегральной кривой и перестаёт иметь
что-либо общее с точным решением
.
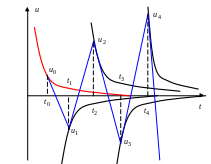
Рис. 4.4. “Разболтка” при решении “жёсткого” ОДУ
явным методом Эйлера.
Предотвратить “разболтку” можно, используя неявные схемы интегрирования дифференциальных уравнений. Например, неявный метод Эйлера применительно к уравнению
даёт
,
откуда находим
.
Так как
,
то
при любом
.
Поведение приближённого решения в этом
случае иллюстрирует рис. 4.5.
Неявная схема Эйлера реально не применяется, но разработаны эффективные неявные многошаговые методы решения “жёстких” уравнений. В программе MathCAD для решения “жёстких” ОДУ предназначены функции Stiffb, stiffb, реализующие алгоритм Булирша-Штёера, и функции Stiffr, stiffr, реализующие алгоритм Розенброка. В программе Matlab имеются встроенные функции ode15s, ode23s, ode23t, ode23tb, решающие “жёсткие” ОДУ по методам Гира и Розенброка.
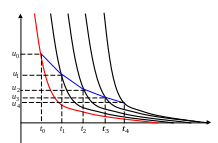
Рис. 4.5 Решение “жёсткого” ОДУ неявным методом Эйлера
ЛАБОРАТОРНАЯ РАБОТА №4
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ «ЖЁСТКОГО» ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 2-го ПОРЯДКА
Цель работы.
Сравнительный анализ численных решений
«жёсткого» ОДУ 2-го порядка
,
полученных методами Рунге-Кутты и
Розенброка.
Порядок выполнения.
1.Представить ОДУ своего варианта (Приложение 4.1) в виде эквивалентной системы двух уравнений второго порядка.
2.Численно решить
полученную систему в программе MathCAD
по методу Рунге – Кутты с помощью функции
rkfixed
при трёх значениях шага
.
3.Численно решить ту же систему с помощью функции Rkadapt.
4.Численно решить ту
же систему по методу Розенброка с помощью
функции Stiffr.
Для обращения к функции предварительно
необходимо определить матрицу Якоби
,
которая строится следующим образом.
Матрица
правых частей эквивалентной системы
рассматривается как функция времени и
компонент
вектора
,
По определению,
.
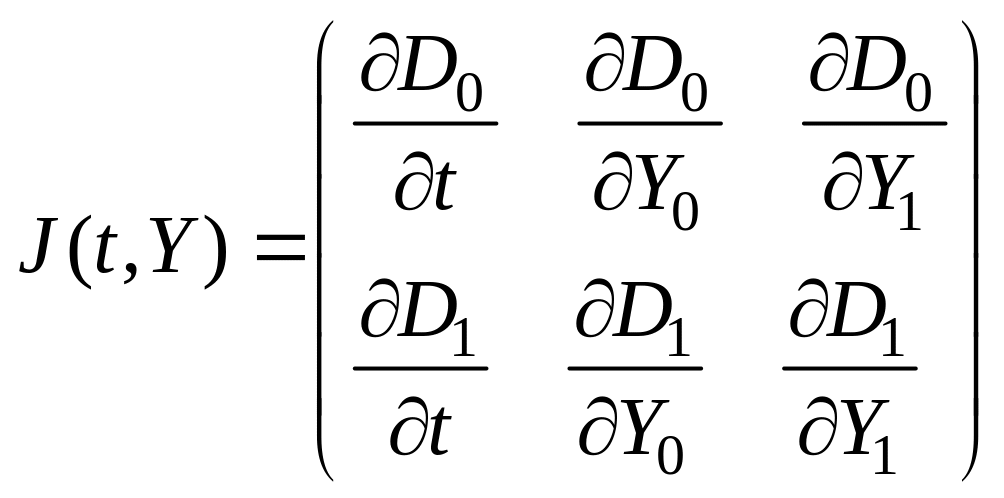Для линейного неоднородного ОДУ 2-го
порядка с постоянными коэффициентами
Формат обращения к функции Stiffr следующий:
где
- интервал, на котором ищется решение,
N - число шагов на этом
интервале,
- вектор начальных значений,
,
,
5.Решить уравнение аналитически.
6.Сравнить численные решения с точным аналитическим решением.
7.Сделать выводы по результатам работы.
Приложение 4.1
Варианты заданий к Лабораторной работе №4.
№ |
a1 |
a2 |
y(a) |
|
a |
|
1 |
2000 |
0 |
1 |
1 |
0 |
|
2 |
-4000 |
4 |
0 |
1 |
0 |
|
3 |
20000 |
0 |
0 |
0 |
/2 |
|
4 |
1000 |
1 |
3 |
0 |
-/2 |
|
5 |
2500 |
5 |
0 |
0 |
1 |
|
6 |
-4400 |
4 |
1 |
1 |
0.3 |
|
7 |
6000 |
13 |
-1 |
1 |
0.25 |
|
8 |
1500 |
1 |
4 |
1 |
/2 |
|
9 |
2500 |
5 |
6 |
2 |
-/2 |
|
10 |
-4000 |
8 |
0 |
2 |
1 |
|
11 |
2700 |
0 |
0 |
2 |
0 |
|
12 |
-400 |
4 |
-1 |
0.5 |
2 |
|
13 |
1200 |
1 |
1 |
1 |
/2 |
|
14 |
2200 |
5 |
4 |
-0.5 |
-/2 |
|
15 |
6300 |
13 |
5 |
2 |
0.8 |
|
16 |
-4400 |
8 |
0 |
0.5 |
0.75 |
|
17 |
2100 |
0 |
1 |
1 |
-1 |
|
18 |
-4400 |
4 |
-1 |
0 |
/2 |
|
19 |
6600 |
13 |
-2 |
2 |
1 |
|
20 |
1600 |
1 |
8 |
0.5 |
0.3 |
|
21 |
-3000 |
3 |
0 |
-1 |
0.4 |
|
22 |
1000 |
2 |
9 |
0.6 |
0.4 |
|
23 |
-2000 |
2 |
-1 |
0 |
0.3 |
|
24 |
17000 |
-1 |
0 |
0 |
-1 |
|
25 |
5900 |
12 |
4 |
1 |
0.7 |
|
