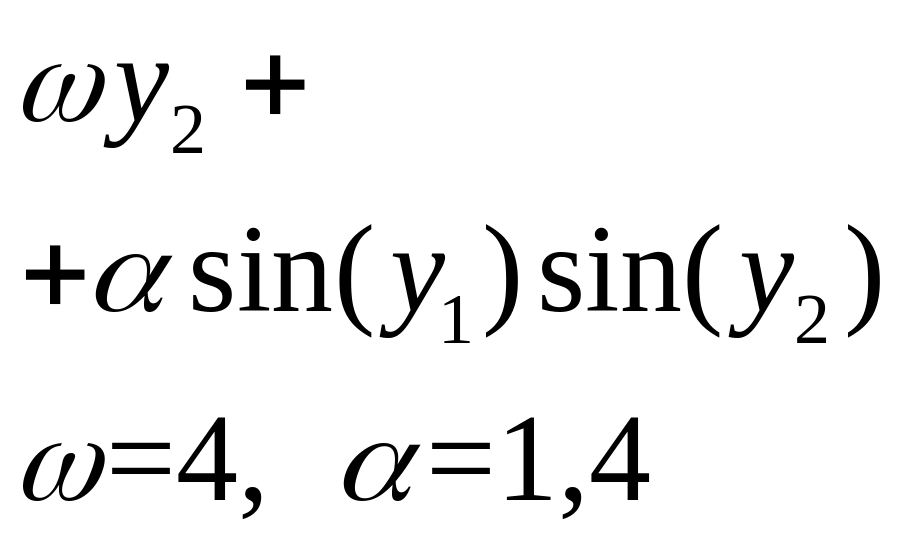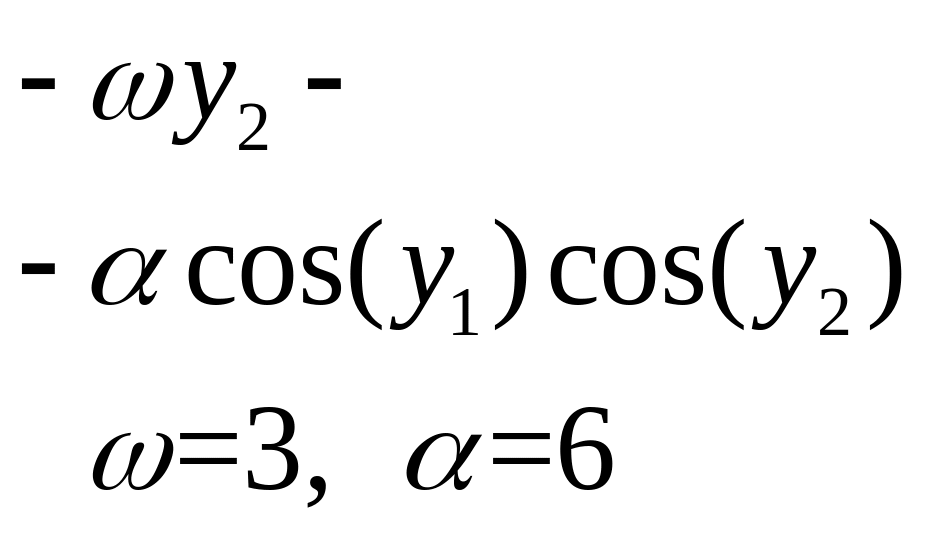4.3 Явные многошаговые методы решения задачи коши.
Ещё раньше, чем методы Рунге – Кутты, около 1855 г., Дж. К. Адамсом был предложен способ построения явных многошаговых алгоритмов решения задачи Коши. В общем случае они могут быть записаны в виде
(4.10)
Согласно (4.10), значение функции в узле выражается через её значение в q предшествующих узлах. Поэтому алгоритм Адамса состоит из двух частей:
-
стартовой процедуры для определения
;
- вычисления по многошаговой формуле (4.10).
Стартовая процедура должна основываться на каком-либо другом численном методе, либо q начальных значений должны задаваться априорно. Часто эти начальные значения находят по методу Рунге – Кутты.
В зависимости от числа слагаемых q в скобках правой части (4.10) методы называются q – членными. Порядок точности их равен q.
Явные
многошаговые методы относятся к
алгоритмам типа предиктор-корректор.
Они вычисляют значение решения
не непосредственно по формуле (4.10), а в
два этапа. Сначала находится
экстраполированное значение
(предиктор), которое затем уточняется
интерполированием (корректор). Прояснить
смысл процедур экстраполяции и
интерполяции можно, записав формальное
решение
в виде
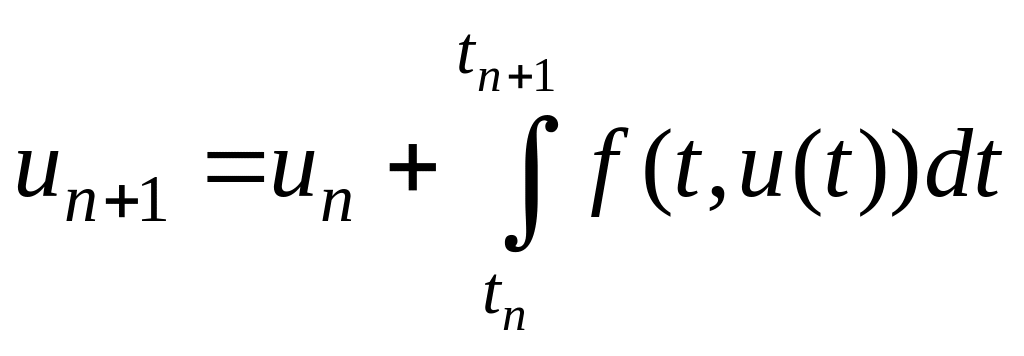(4.11)
Подынтегральная
функция при
не известна.
Поэтому её интерполируют по точкам
полиномом
-го
порядка на интервале
и экстраполируют за
пределы
этого интервала (рис. 4.3а).
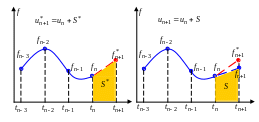
Рис. 4.3 Графическая интерпретация четырёхшагового алгоритма
предиктор-корректор
Предсказанное решение в точке , согласно (4.11), есть
где
- площадь под экстраполированной частью
функции
.
После
этого функция
интерполируется на интервале
по точкам
полиномом того же порядка, а скорректированное
решение в точке снова находится по
(4.11),
где
- площадь под интерполированной функцией
на интервале
.
Если
интерполировать
полиномом Ньютона третьего порядка на
равномерной сетке с шагом
,
получим алгоритм Адамса-Башфорта-Mоултона
Явные многошаговые методы Адамса, так же как и предложенные позже методы Милна, Хэмминга, Нистрёма, в целом менее эффективны по сравнению с методами Рунге – Кутты того же порядка и в настоящее время используются редко.
ЛАБОРАТОРНАЯ РАБОТА №2
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ СИСТЕМЫ ДВУХ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Цель работы. Программирование метода Хойна и применение разработанной программы к решению системы ОДУ 1-го порядка
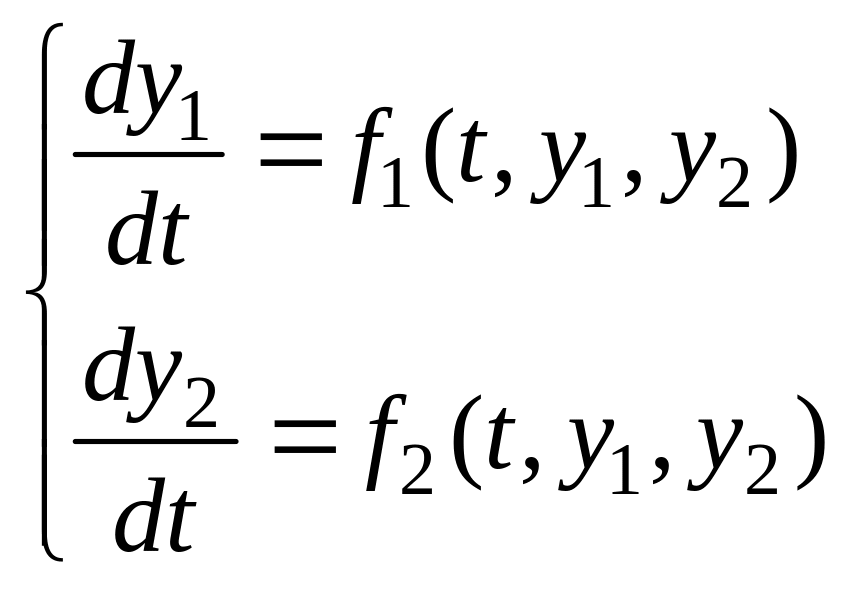
на интервале
с начальными условиями.
Порядок выполнения.
1.Изучить теоретический материал по п.4.1.
2.Написать MathCAD-программу численного решения по методу Хойна системы двух ОДУ. Пример MAthCAD-программы, реализующей метод Хойна, приведён в Приложении 2.2
3.Решить с её помощью систему ОДУ своего варианта (Приложение 2.1).
4. Решить эту же систему ОДУ с использованием MathCAD-функции rkfixed. Пример решения системы ОДУ с помощью функции rkfixed, приведён в Приложении 2.3.
5.Написать Matlab-программу численного решения по методу Хойна системы двух ОДУ. Пример Matlab-программы, реализующей метод Хойна, приведён в Приложении 2.4
6.Решить с её помощью систему ОДУ своего варианта.
7. Решить эту же систему ОДУ с использованием Matlab-функции ode45. Пример решения системы ОДУ с помощью функции ode45, приведён в Приложении 2.5.
8.Сравнить полученные
решения, построив их графики в одних
координатных осях. Построить графики
относительных погрешностей
,
,
где
- решения системы по методу Хойна,
- её решения по методу Рунге-Кутты.
9.Сделать выводы по результатам работы.
Приложение 2.1
Варианты заданий к Лабораторной работе №2
№ |
|
|
|
|
|
|
1 |
|
|
1 |
0.7 |
-1 |
20 |
2 |
|
|
0.5 |
1.5 |
0 |
5 |
3 |
|
|
-1 |
1 |
0 |
2 |
4 |
|
|
1 |
0 |
0 |
5 |
5 |
|
|
2 |
1 |
0 |
4 |
6 |
|
|
1 |
3 |
0 |
5 |
7 |
|
|
1 |
-1 |
0 |
10 |
8 |
|
|
1 |
-2 |
0 |
5 |
9 |
|
|
3 |
0.5 |
0 |
5 |
10 |
|
|
1 |
2.5 |
0 |
7 |
11 |
|
|
1 |
1.7 |
0 |
5 |
12 |
|
|
0 |
2 |
0 |
5 |
13 |
|
|
-1 |
2 |
0 |
10 |
14 |
|
|
-2 |
2 |
0 |
10 |
15 |
|
|
0 |
2 |
0 |
10 |
16 |
|
|
3 |
2 |
0 |
6 |
17 |
|
|
1 |
2 |
0 |
10 |
18 |
|
|
3 |
2 |
0 |
10 |
19 |
|
|
0 |
0 |
0 |
4 |
20 |
|
|
2 |
2 |
0 |
10 |
21 |
|
|
2 |
-1 |
0 |
10 |
22 |
|
|
2 |
-1 |
0 |
10 |
23 |
|
|
2 |
1 |
0 |
10 |
24 |
|
|
0 |
0 |
1 |
3 |
25 |
|
|
0.5 |
0.5 |
1 |
3 |
Приложение 2.2
Пример MathCAD-программы, реализующей метод Хойна
Вычисляем
пошагово узловые точки и
и
значения искомых функций
и
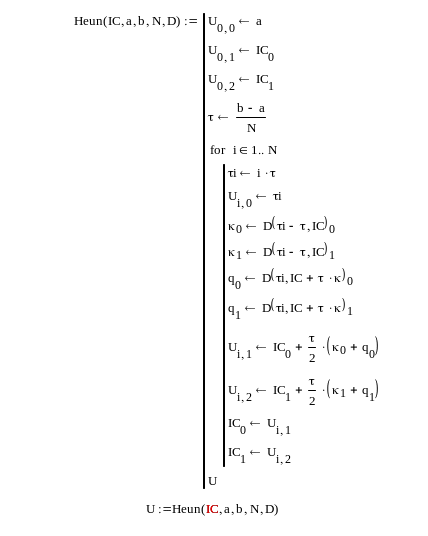
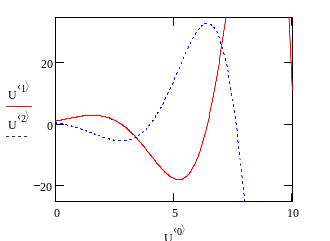
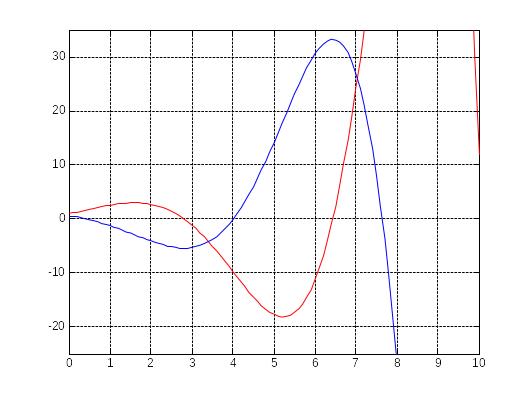
Строим графики полученных решений
Приложение 2.3
Пример MathCAD-программы решения системы дифференциальных уравнений по методу Рунге-Кутты
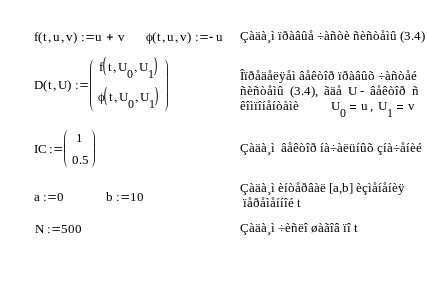
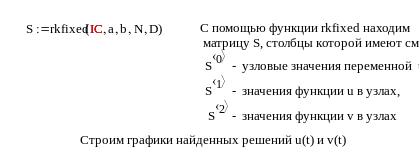
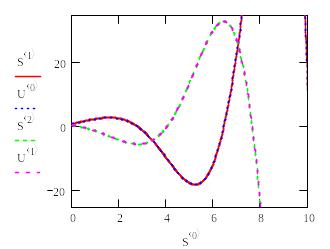
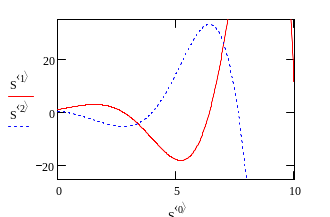
Сопоставляем
графики решений, найденных по
методам Хойна и Рунге-Кутты
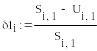
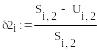
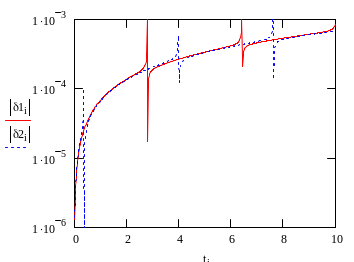
Вычисляем
относительные погрешности
Приложение 2.4
Пример Matlab-программы решения системы дифференциальных уравнений по методу Хойна
%Программа Heun решает систему 2-x ОДУ 1-го порядка
t0=0.0; %левый край интервала
tf=10.0; %правый край интервала
u0=2.0; %начальное значение первой функции
v0=1.0; %начальное значение второй функции
N=100; %число временных шагов
[t,U]=ODE_Heun(N,int,IC);% численное интегрирование системы ОДУ
plot(t,U(:,1),'r',t,U(:,2),'b');grid on;axis([t0 tf -25 35])
title('Графики решения системы двух ОДУ 1-го порядка')
xlabel('t'); ylabel('u, v')
legend('u(t)','v(t)')
function [t,U]=ODE_Heun(N,int,IC)
i=0:N;
tau=(int(2)-int(1))/N;
t=int(1)+tau.*i;
U(1,1)=IC(1);
U(1,2)=IC(2);
for j=1:N
k1=F1(t(j),U(j,1),U(j,2));
q1=F2(t(j),U(j,1),U(j,2));
k2=F1(t(j)+tau,U(j,1)+tau*k1,U(j,2)+tau*q1);
q2=F2(t(j)+tau,U(j,1)+tau*k1,U(j,2)+tau*q1);
U(j+1,1)=U(j,1)+1/2.*tau.*(k1+k2);
U(j+1,2)=U(j,2)+1/2.*tau.*(q1+q2);
end
function f=F1(t,u,v)
f=u+v;
function f=F2(t,u,v)
f=-u;
Приложение 2.5
Пример Matlab-программы решения системы дифференциальных уравнений по методу Рунге-Кутты
%Программа ODESystem решает систему ОДУ 1-го порядка
t0=0; % левый край интервала
tf=10; %правый край интервала
u0=1.0; %начальное значение первой функции
v0=0.5; %начальное значение второй функции
[t,U]=ode45('SODE',[t0,tf],[u0,v0]);% численное интегрирование системы ОДУ
plot(t,U(:,1),'r',t,U(:,2),'b');grid on;axis([t0 tf -25,35])
title('Графики решения системы двух ОДУ 1-го порядка')
xlabel('t'); ylabel('u, v')
legend('u(t)','v(t)')
function f = SODE(t,u)
%Система двух ОДУ 1-го порядка
f=[u(1)+u(2);-u(1)];
