Глава 3. Метод конечных разностей

3.1. Сетки и сеточные функции

Пространственной сеткой называется множество точек пространства, используемых для приближенного представления непрерывной функции, описывающей координатную зависимость физической величины.

Временнóй сеткой называется множество моментов времени, используемых для приближенного представления функции, описывающей временнýю зависимость физической величины.

Сами пространственные точки и моменты времени называются узлами сетки. Пространственные узлы в определённый момент времени образуют пространственный слой.

Функция , заданная в узлах пространственно-временной сетки, называется сеточной.

При численном решении математических задач используются равномерные и неравномерные сетки.

Равномерная сетка получается разбиением интервала изменения переменой (координаты или времени) на одинаковых ячеек.

Неравномерная сетка образуется при разбиении интервала на неодинаковые ячейки.

В дальнейшем будем рассматривать только равномерные сетки. Сеточные узлы могут быть расположены в ячейках двумя способами – на границе ячейки (рис. 3.1а) либо в её центре (рис. 3.1б). В первом случае сетку назовём граничной, число её узлов на единицу больше числа ячеек N. Размер ячейки, называемый шагом сетки, равен . Узлы расположены в точках

Во втором случае сетку буде называть центрирующей. Число ячеек равно числу узлов, шаг равен , а узлы расположены в точках

Для более точной аппроксимации граничных условий центрирующую сетку дополняют двумя вспомогательными узлами, расположенными в точках и (рис. 3.1в).

Рис.3.1 Три типа сеток

Значения сеточной функции в узлах одномерной сетки будем обозначать .

Функцию, зависящую от двух переменных, аппроксимируем сеточной функцией, заданной в узлах двумерной сетки. Для этого задаём размер шага по каждой переменной. Если обе переменные - пространственные, например, x и y, то, обозначая шаги через и , узлы зададим точками (рис.3.2),

,

Рис. 3.2 Двумерная пространственная сетка

Значение функции в узле, заданном индексами i и j будем обозначать .

Если функция u зависит от пространственной переменной x и времени t, то разбиение области её определения на ячейки производится аналогично. Шаги обозначаем и , узел задаём соотношениями

,

а значение функции в узле обозначаем (рис. 3.3). Число узлов двумерной сетки равно

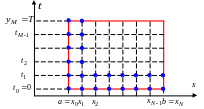
Рис. 3.3 Пространственно-временнáя сетка

3.2. Аппроксимация производных

Производные функции в точке равномерной сетки можно аппроксимировать несколькими способами. Предпочесть следует тот из них, который обеспечивает наивысшую точность аппроксимации, то есть наименьшую разность между точным значением производной и её приближённым значением .

Первую производную в узлах сетки можно аппроксимировать тремя способами:

- посредством правых разностей

(3.1)

- посредством левых разностей

(3.2)

- посредством центральных разностей

(3.3)

Графическая интерпретация формул (3.1) – (3.3) показана на рис. 3.4. Из рис. 3.4 видно, что формула (3.3) обеспечивает более точную аппроксимацию производной в узле по сравнению с формулами (3.1) и (3.2), так как наклон отрезка АС гораздо ближе к наклону касательной .

Количественные критерии точности аппроксимации найдём, разложив функции и в ряд Тейлора вплоть до третьего порядка по ,

(3.4)

(3.5)

Здесь - точные значения производных в узле .

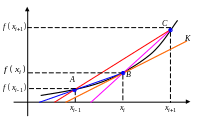
Рис. 3.4 Аппроксимации первой производной

Подставив (3.4) и (3.5) в (3.1) – (3.3), получим

(3.6)

(3.7)

(3.8)

Таким образом, погрешность аппроксимации правыми и левыми разностями пропорциональна , тогда как при аппроксимации центральными разностями она пропорциональна . При уменьшении шага в 10 раз ошибка аппроксимаций (3.1) и (3.2) уменьшается также в 10 раз. В то же время при аппроксимации (3.3) ошибка уменьшается в 100 раз, поэтому центральноразностная аппроксимация предпочтительнее.

При аппроксимации второй производной вариантов побольше. Её можно аппроксимировать с помощью:

а) правой разности правых первых производных

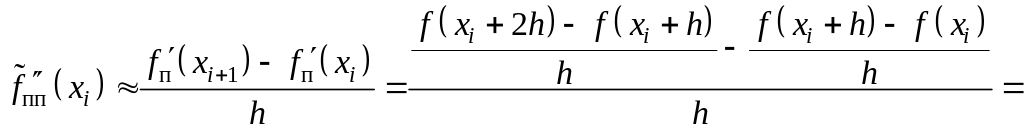
(3.9)

б) либо левой разности левых первых производных

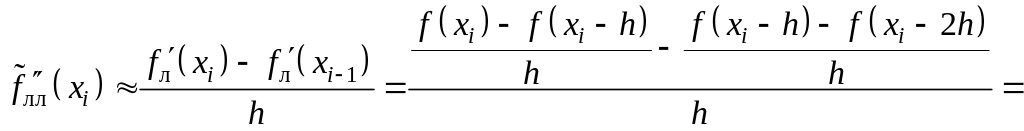
(3.10)

в) либо левой разности правых первых производных

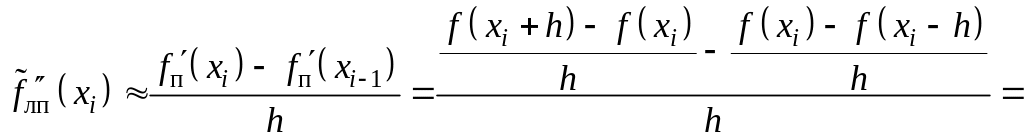
г) либо правой разности левых первых производных

д) либо центральной разности правых первых производных

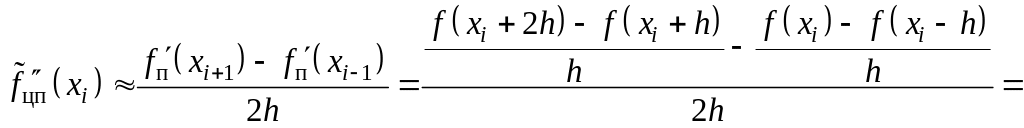
(3.12)

е) либо центральной разности левых первых производных

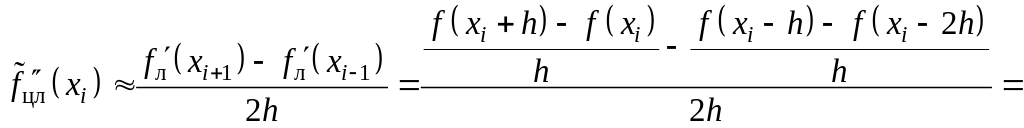
(3.13)

Используя разложения (4.4), (4.5), получим оценки точности аппроксимаций вторых производных,

(3.14)

(3.15)

(4.16)

(4.17)

(4.18)

Из (3.14) (3.18) следует, что наилучшей является левоправая или праволевая аппроксимация второй производной . Вносимая ею погрешность пропорциональна .

Совершенно аналогично можно получить аппроксимации с точностью третьей и четвёртой производных:

(3.19)

(3.20)

Задача: Вывести самостоятельно формулы (3.19) и (3.20) и оценить их точность по остаточному члену разложения Тейлора по степеням .

Производные выше четвёртой в модельных задачах встречаются крайне редко. В дальнейшем будем использовать аппроксимации (3.3), (3.11), (3.19) и (3.20), не указывая индексы,

Из оценок погрешностей этих аппроксимаций

можно было бы заключить, что они могут быть сделаны сколь угодно малыми только за счёт уменьшения шага . Это утверждение верно, если арифметические операции выполняются над числами, заданными с любой, сколь угодно высокой, точностью. Для десятичного числа это значит, что его можно вычислить с неограниченным числом знаков после запятой. В компьютерном представлении, однако, число значащих цифр вещественного числа ограничено. Из 64 разрядов регистра процессора или ячейки памяти один разряд отводится под знак числа , семь разрядов – под его порядок , ещё один разряд – под знак порядка, а остальные 55 – под мантиссу , так что в десятичной записи мантисса содержит

значащих цифр. Поэтому разность двух близких чисел и не может быть сделана меньшей, чем так называемое машинное эпсилон Следовательно, при отношение имеет порядок 1, а при - может существенно превышать единицу. Вследствие накопления ошибок округления происходит катастрофическая потеря точности при вычислении производной. В интервале существует оптимальное значение шага, при котором точность вычисления производной наивысшая. Причём оптимумы для производных разных порядков не совпадают. Эти оптимумы определяются в Лабораторной работе №1.

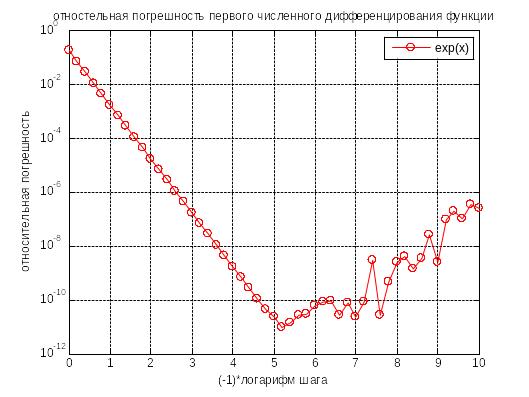
ЛАБОРАТОРНАЯ РАБОТА №1

ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ШАГА ПРИ ЧИСЛЕННОМ ДИФФЕРЕНЦИРОВАНИИ

Цель работы – определить оптимальный размер шага при разностной аппроксимации первой, второй, третьей и четвёртой производных функций , , .

Необходимый инструментарий – персональный компьютер с установленными программами MathCAD и Matlab.

Порядок выполнения.

1. В программе MathCAD написать программу вычисления производных функции по формулам (4.3), (4.11), (4.19), (4.20) и их относительных погрешностей

2. Принять 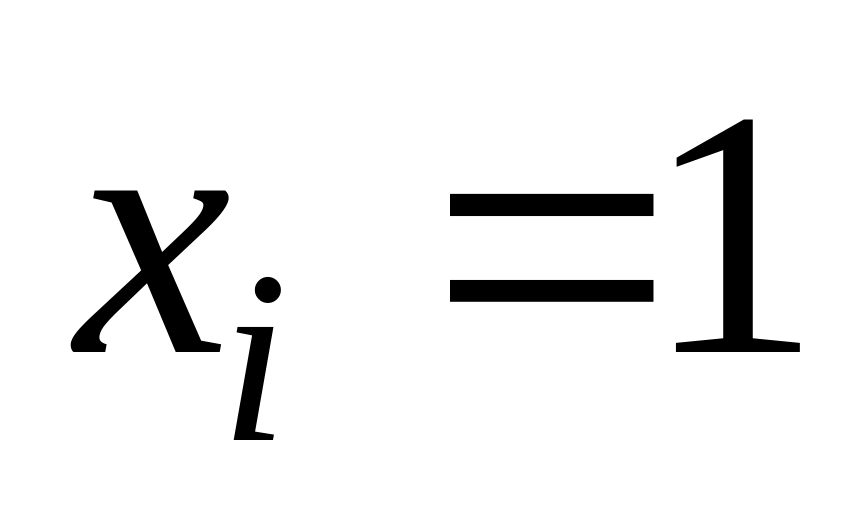. Изменяя шаг в интервале от 1 до , построить графики зависимостей 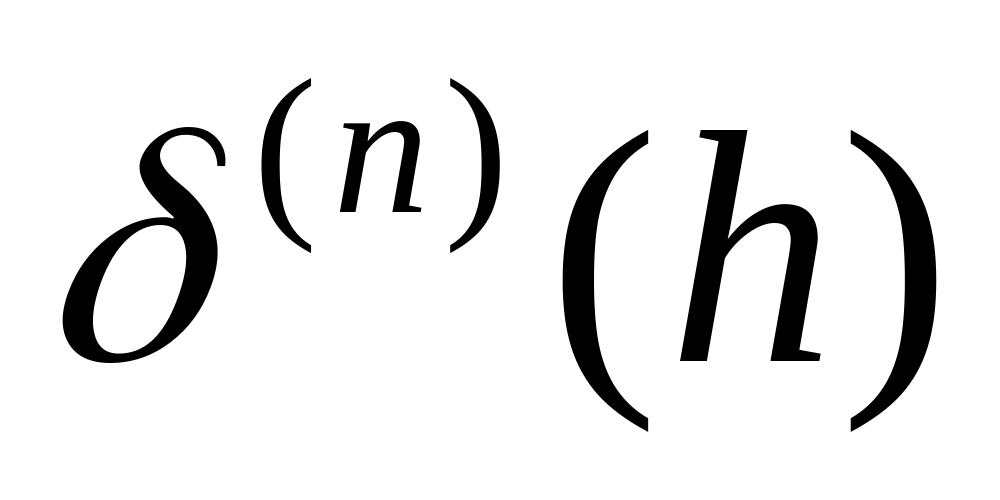. Определить по ним оптимальное значение шага для производных каждой функции.

3. Повторить п.2 для 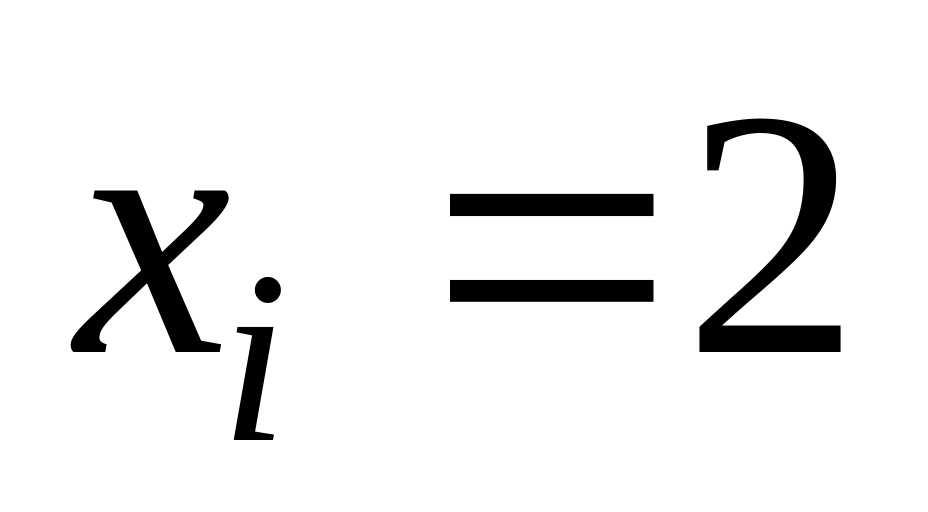и .

4. Сделать выводы по результатам работы.

Пример MathCAD-программы для вычисления конечноразностной аппроксимации первой производной:

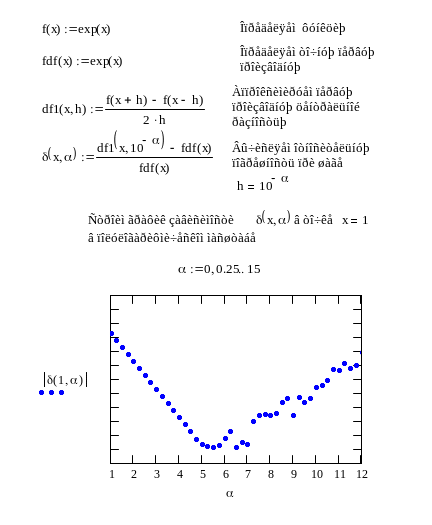
Пример Malab-программы для вычисления конечноразностной аппроксимации первой производной:

%Программа Numderiv

%вычисляет относительные погрешности...

%численного дифференцирования 1-го порядка

x=1;

n=0:0.2:10;

h=10.^-n;

del1 = DEL1(x,h);

semilogy(n,del1,'ro-');grid on; axis([0 10 10^-12 1])

function DEL1=DEL(x,h)

%вычисление относительной погрешности...

%численного дифференцирования в заданной точке x

df01=d1fun(x);

fr=fun(x+h);fl=fun(x-h);

df1=(fr-fl)./(2.*h);

DEL1=abs((df1-df01)./df01);

function f=fun(x)

%вычисдение значений функции

f=exp(x);

function f=d1fun(x)

%вычисление значений 1-й производной

f=exp(x);