5. Второй дифференциал

Вполне аналогично тому, как это было сделано для функции одной переменной, вводится понятие дважды дифференцируемой функции многих переменных.

Если в окрестности данной точки приращение функции можно представить в виде суммы линейной формы относительно вектора dx : А₁dх₁ + А₂dх₂ + … + А_ndх_n , а также половины квадратичной формы относительно вектора dx : (dx H(x) dx) и ошибки , порядок малости которой выше второго − o(dx′ dx), то функция называется дважды дифференцируемой в точке x₀, линейная часть приращения называется первым дифференциалом и обозначается dF, квадратичная часть приращения (dx H(x) dx)называется вторым дифференциалом и обозначается d²F:

dF(x₀) = dx₁ + dx₂ + …+ dx_n = ( dx)

= (dx dx)

И приращение для дважды дифференцируемой функции имеет вид:

F=F(x₀+x)– F(x₀)=

6.Условия экстремума

Стационарность: если в некоторой точке x₀ все частные производные равны нулю  градиент равен нуль-вектору  первый дифференциал тождественно равен нулю dF ≡ 0 − то такая точка называется стационарной.

Необходимое условие экстремума − стационарность. Другими словами – в точке, в которой хоть одна из частных производных существует и не равна нулю экстремума быть не может.

Достаточное условие экстремума: второй дифференциал как квадратичная форма знакоопределен в стационарной точке.

При этом, если второй дифференциал положительно определен, в данной стационарной точке имеем минимум, если же он отрицательно определен – в данной стационарной точке имеем максимум.

Формулы дифференцирования

C	C=0
u	u
u2	2u u
	u
un	n un-1 u
cu	c u
αu+βv	αu+βv
uv	uv+ uv
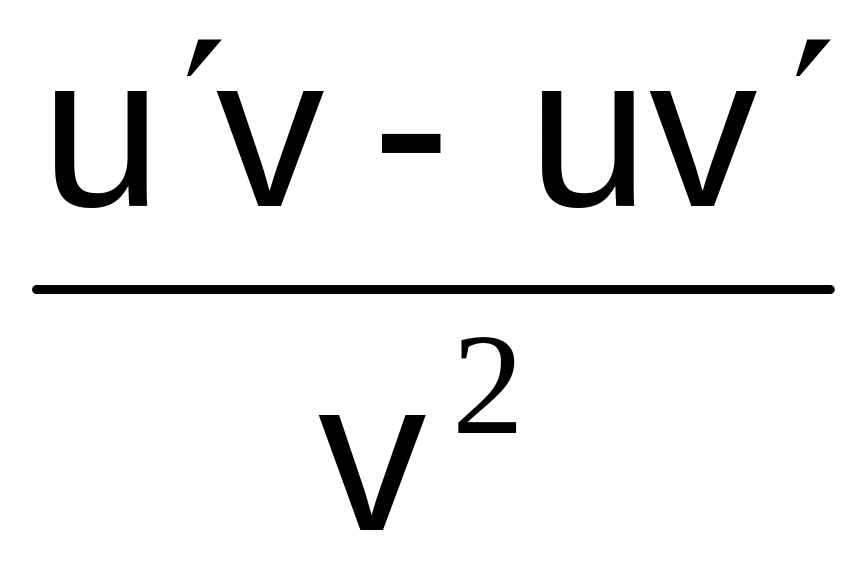
eu	eu u
lnu	u
sinu	cosu u
cosu	– sinu u
tgu
ctgu
arcsinu	u
arccosu	u
arctgu	u

Формулы интегрирования

1.

2.

3.

4.

5.

6.

7.

8.

Теория поля

1. Оператор набла

Оператором  (набла) называется псевдовектор:



 записывается как вектор: в виде столбца или строки с штрихом вверху  символом транспозиции, а является дифференциальным оператором. Применение оператора  к некоторому объекту записывается в виде умножения на , и мы назвали его псевдовектором, поскольку все случаи его применения формально аналогичны умножению векторов. Как известно, для векторов определены три вида умножения: умножение на скаляр, скалярное произведение и векторное произведение. Соответственно, для оператора  определены три операции:

u =(u/x,u/y,u/z) = gr(u) =

(v) = = div v

[v] = = rot v

Результат первой операции называется градиент, второй – дивергенция, третьей – ротор.

2. Стандартные значения

Помня, что r = x = (x, y, z)′ - текущий радиус-вектор, - его длина, вектор dr = - его приращение, а dr - длина приращения, вычислим результаты применения оператора  к нашим стандартным переменным

r = r/r

div r = n, где n  размерность пространства,

rot r = [r] =

3. Потенциальное поле

Поле называется потенциальным тогда и только тогда, когда существует функция u(r), такая, что v(r) = u(r), при этом функция u(r) называется потенциалом поля.

Поле потенциально тогда и только тогда, когда оно безвихревое, т.е. [v] = .

Для потенциальных полей du = u/x dx + u/y dy +u/z dz = (u dr) = (v dr)

4. Ньютоновский (кулоновский) потенціал

Функция является потенциалом для поля гравитационных сил:

поэтому функция , где А  некоторая константа, называется ньютоновским (кулоновским) потенциалом.

5.Теорема о потенциале.

Пусть нам дано некоторое дифференцируемое поле F. Тогда следующие четыре утверждения являются эквивалентными, т.е. все они выполнены или не выполнены одновременно:

1. поле F является потенциальным, т.е. существует функция u, такая, что F = u

2. величина интеграла определяется выбором начальной и конечной точки пути интегрирования, и не зависит от кривой, их соединяющей

3. в поле F циркуляция по любому замкнутому контуру равна нулю = 0

4. поле F является безвихревым, т.е. : rot v = [v] = ≡